二次函数一直都是中考中的必考内容,而且在中考试卷中占有很大比值。所以中学生学好二次函数,非常重要。下面小编整理了二次函数相关内容,仅供参考。
二次函数的概念

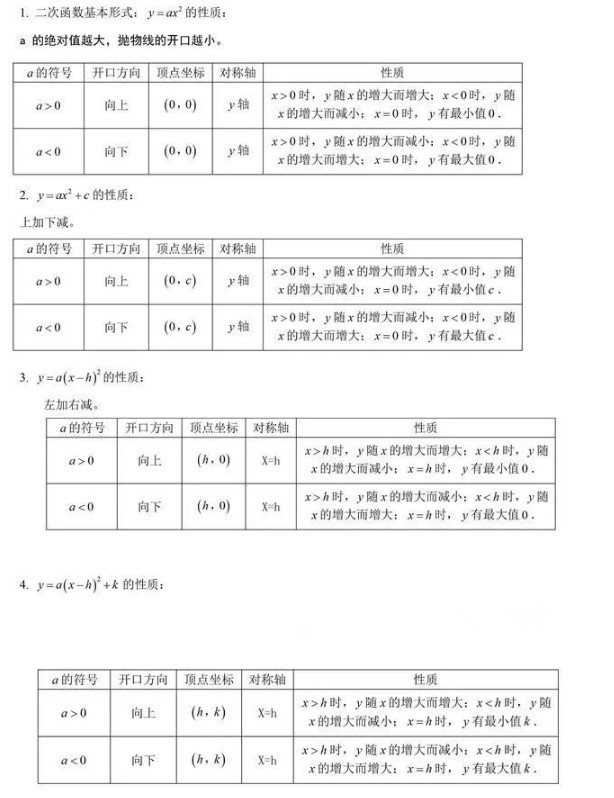
二次函数的基本形式
二次函数解析式的表达方式

二次函数图像的对称

如图,在平面直角坐标系中,抛物线C1:y=ax2+x-1经过点A(-2,1)和点B(-1,-1),抛物线G2:y=2x2+x+1,动直线x=t与抛物线交于点N,与抛物线C2交于点M。
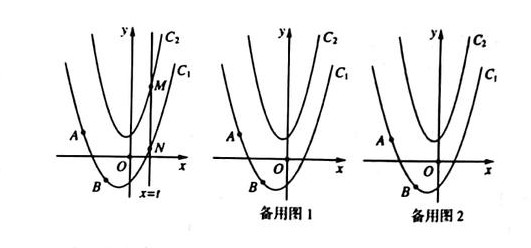
(1)求抛物线C1的表达式;
(2)直接用含t的代数式表示线段MN的长;
(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值;
(4)在(3)的条件下,设抛物线C1与y轴交于点P,点M在y轴右侧的抛物线C2上,连接AM交y轴于点K,连接KN,在平面内有一点Q,连接KQ和QN,当KQ=1且∠KNQ=∠BNP时.请直接写出点Q的坐标.
解题:
(1)因为抛物线C1:y=ax2+bx-1经过点A(2,1)和B(-1,-1),4a-2b-1=1,
a-b-1=-1,a=1,b=1.
抛物线C的表达式为y=x2+x-1
(2)M(t,2t2+t+1)N(t,t2+t-1),MN=t2+2.
(3)共分两种情况
①当∠ANM=90°,AN=MW时,依题意N(t,t2+1-1),A(-2,1),
AN=t+2,由(2)得MN=t2+2,联立解得t=0,t=1,
t=0时,∠AMN=90°,不符合题意舍去,t=1;
②当∠AMN=90°,AM=MN时,
依题意M(1,t2+t+1),A(-2,1),
AM=t-(-2)=t+2,
由(2)得MN=t2+2
t=0,t=1.
t=1时,∠AM=90°,不符合题意舍去,t=0,
综上所述,的值为0或1.
(4)(0,2),(-1,3),(4/5,12/5),(3/5,19/5)

一般地,自变量x和因变量y之间存在如下关系:y=ax²+bx+c(a,b,c为常数,a≠0,且a决定函数的开口方向,a>0时,开口方向向上,...

二次函数顶点坐标公式:y=a(x-h)^2+k,[抛物线的顶点P(h,k)],一般式:y=ax^2+bx+c(a,b,c为常数,a≠0),二...

学好二次函数的方法:二次函数的表达式有一般式、顶点式和交点式,我一定要记清楚,并且知道三种表达式之间的转化关系,尤其是一般式要能熟练地化成顶...

初三二次函数应用题解题技巧:待定系数法型,题设明确给出两个变量间是二次函数关系,和几对变量值,要求求出函数关系式,并进行简单的应用。解答的关...

二次函数图象是抛物线,是轴对称性图形。y=ax的图象是最简单的二次图像,学习也较容易。顶点坐标为(0,0),即原点;对称轴为y轴,开口由a的...

二次函数是初三数学的重点,学生们一定要扎实掌握,小编整理了一些重要的二次函数知识点。

小编为大家整理了二次函数的数学知识点,大家跟随小编一起来学习一下吧。

小编为大家整理了二次函数的数学知识点,大家跟随小编一起来看一下吧。