因式分解公式有:平方差公式:a²-b²=(a+b)(a-b)。完全平方公式:a²+2ab+b²=(a+b)²。立方和公式:a³+b³=(a+b)(a²-ab+b²)。立方差公式:a³-b³=(a-b)(a²+ab+b²)。完全立方和公式:a³+3a²b+3ab²+b³=(a+b)³。完全立方和公式:a³+3a²b+3ab²+b³=(a+b)³。

1、平方差公式:a²-b²=(a+b)(a-b)。
2、完全平方公式:a²+2ab+b²=(a+b)²。
3、立方和公式:a³+b³=(a+b)(a²-ab+b²)。
4、立方差公式:a³-b³=(a-b)(a²+ab+b²)。
5、完全立方和公式:a³+3a²b+3ab²+b³=(a+b)³。
6、完全立方差公式:a³-3a²b+3ab²-b³=(a-b)³。
7、三项完全平方公式:a²+b²+c²+2ab+2bc+2ac=(a+b+c)²。
8、三项立方和公式:a³+b³+c³-3abc=(a+b+c)(a²+b²+c²-ab-bc-ac)。
1,因式分解的定义:把一个多项式在一个范围化为几个整式的积的形式,这种式子变形叫做这个多项式的因式分解,也叫作把这个多项式分解因式。
2,因式分解因式的作用:分解是中学数学中最重要的恒等变形之一,它被广泛地应用于初等数学之中,在数学求根作图、解一元二次方程方面也有很广泛的应用,是解决许多数学问题的有力工具。
3,因式分解的意义:因式分解方法灵活,技巧性强。学习这些方法与技巧,不仅是掌握因式分解内容所必需的,而且对于培养解题技能、发展思维能力都有着十分独特的作用。学习它,既可以复习整式的四则运算,又为学习分式打好基础;学好它,既可以培养学生的观察、思维发展性、运算能力,又可以提高综合分析和解决问题的能力。

把一个多项式在一个范围(如实数范围内分解,即所有项均为实数)化为几个整式的积的形式,这种式子变形叫做这个多项式的因式分解,也叫作把这个多项式...

因式分解的方法有:提公因式法,如果一个多项式的各项都含有公因式,就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。应用公式法,由...

对一些简单的三次方程能用因式分解求解,用因式分解法求解很方便,直接把三次方程降次。例如:解方程x^3-x=0,对左边作因式分解,得x(x+1...

很多同学都学过因式分解,那么因式分解有哪些技巧?大家一起来看看吧。
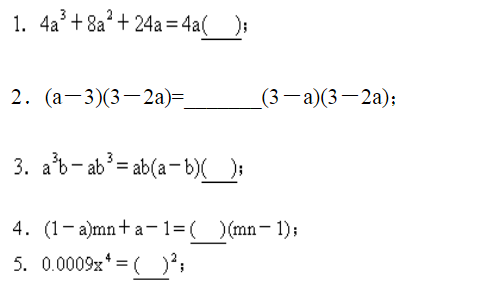
小编为大家整理了因式分解的一些知识,大家快来跟着小编一起学习一下吧。

小编为大家整理了因式分解的方法的相关知识点,大家快来跟着小编一起学习一下吧。

很多同学都学习了因式分解,小编整理了一些因式分解的口诀,大家一起来看看吧。

因式分解是数学中常用的计算方法,因式分解包括提公因式法、公式法、十字相乘法、待定系数法、换元法等。