因式分解的方法有:提公因式法,如果一个多项式的各项都含有公因式,就可以把这个公因式提出来,从而将多项式化成两个因式乘积的形式。应用公式法,由于分解因式与整式乘法有着互逆的关系,把乘法公式反过来就可以用来把某些多项式分解因式。十字相乘法、分组分解法、配方法、换元法等。

定义:把一个多项式化为几个最简整式的乘积的形式,这种变形叫做把这个多项式因式分解(也叫作分解因式)。
分解要彻底(是否有公因式,是否可用公式)
最后结果只有小括号
最后结果中多项式首项系数为正
公因式:各项都含有的公共的因式叫做这个多项式各项的~.
提公因式法:一般地,如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法叫做提公因式法.
am+bm+cm=m(a+b+c)
具体方法:当各项系数都是整数时,公因式的系数应取各项系数的最大公约数;字母取各项的相同的字母,而且各字母的指数取次数最低的. 如果多项式的第一项是负的,一般要提出“-”号,使括号内的第一项的系数是正的.
由于分解因式与整式乘法有着互逆的关系,如果把乘法公式反过来,那么就可以用来把某些多项式分解因式。
例:分解因式a +4ab+4b
解:a +4ab+4b =(a+2b)
如果多项式的各项有公因式,那么先提公因式;
如果各项没有公因式,那么可尝试运用公式、十字相乘法来分解;
如果用上述方法不能分解,那么可以尝试用分组、拆项、补项法来分解;
分解因式,必须进行到每一个多项式因式都不能再分解为止.
应用因式定理:如果f(a)=0,则f(x)必含有因式(x-a)。如f(x)=x^2+5x+6,f(-2)=0,则可确定(x+2)是x^2+5x+6的一个因式。
x^2+(p q)x+pq型的式子的因式分解
这类二次三项式的特点是:二次项的系数是1;常数项是两个数的积;一次项系数是常数项的两个因数的和.因此,可以直接将某些二次项的系数是1的二次三项式因式分解: x^2+(p q)x+pq=(x+p)(x+q)
对于那些不能利用公式法的多项式,有的可以利用将其配成一个完全平方式,然后再利用平方差公式,就能将其因式分解。
分解因式x +3x-40
解x +3x-40=x +3x+( ) -( ) -40
=(x+ ) -( )
=(x+ + )(x+ - )
=(x+8)(x-5)
要把多项式am+an+bm+bn分解因式,可以先把它前两项分成一组,并提出公因式a,把它后两项分成一组,并提出公因式b,从而得到a(m+n)+b(m+n),又可以提出公因式m+n,从而得到(a+b)(m+n)
分解因式m +5n-mn-5m
解:m +5n-mn-5m= m -5m -mn+5n
= (m -5m )+(-mn+5n)
=m(m-5)-n(m-5)
=(m-5)(m-n)

把一个多项式在一个范围(如实数范围内分解,即所有项均为实数)化为几个整式的积的形式,这种式子变形叫做这个多项式的因式分解,也叫作把这个多项式...

对一些简单的三次方程能用因式分解求解,用因式分解法求解很方便,直接把三次方程降次。例如:解方程x^3-x=0,对左边作因式分解,得x(x+1...

很多同学都学过因式分解,那么因式分解有哪些技巧?大家一起来看看吧。
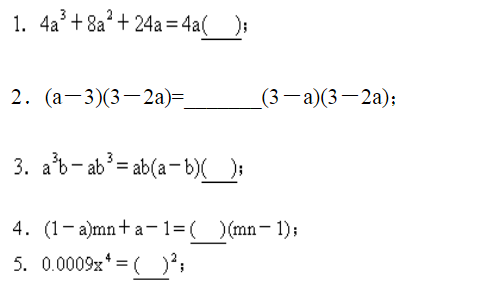
小编为大家整理了因式分解的一些知识,大家快来跟着小编一起学习一下吧。

小编为大家整理了因式分解的方法的相关知识点,大家快来跟着小编一起学习一下吧。

很多同学都学习了因式分解,小编整理了一些因式分解的口诀,大家一起来看看吧。

因式分解是数学中常用的计算方法,因式分解包括提公因式法、公式法、十字相乘法、待定系数法、换元法等。

因式分解并不难,分解方法要记全,各项若有公因式,首先提取莫迟缓,各项若无公因式,套用公式来试验。如果是个二项式,平方差公式要领先,如果是个三...