三角形重心2:1怎么证明

△ABC，E、F是AB，AC的中点。EC、FB交于G。求证：EG=1/2CG。证明：过E作EH∥BF交AC于H。∵AE=BE，EH//BF；∴AH=HF=1/2AF。又∵AF=CF；∴HF=1/2CF。∴HF:CF=1/2。∵EH∥BF；∴EG:CG=HF:CF=1/2。∴EG=1/2CG。

重心的性质

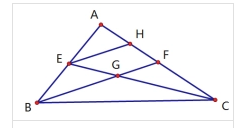
1、重心到顶点的距离与重心到对边中点的距离之比为2︰1。

2、重心和三角形任意两个顶点组成的3个三角形面积相等。即重心到三条边的距离与三条边的长成反比。

3、重心到三角形3个顶点距离的平方和最小。

4、在平面直角坐标系中，重心的坐标是顶点坐标的算术平均数，即其重心坐标为（（X1+X2+X3）/3，（Y1+Y2+Y3）/3）。

5、以重心为起点，以三角形三顶点为终点的三条向量之和等于零向量。