设三角形三边a、b、c,且a>b>c,由a,b,c大于0,又a>b>c,由正弦定理即可证明sinA>sinB>sinC,根据正弦函数的图象和性质即可证明大边对大角,反之即可证明大角对大边。

三角形中大角对大边
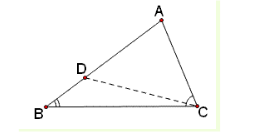
已知:如上图,⊿ABC中,∠ACB>∠B.
求证:AB>AC.
证明:在∠ACB内部作∠BCD=∠B,则DB=DC;
∵AD+DC>AC;(三角形两边之和大于第三边)
∴AD+DB>AC.(等量代换)
即AB>AC.

两组对边分别平行的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;两组对角分别相等的四边形...

两组对边分别平行的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;两条对角线互相平分的四边...

验证两个全等三角形一般用边边边(SSS)、边角边(SAS)、角边角(ASA)、角角边(AAS)、和直角三角形的斜边,直角边(HL)来判定。

三角形中位线定理是三角形的中位线平行于第三边(不与中位线接触),并且等于第三边的一半。

三角形其中一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。接下来分享角平分线性质定理及证明方法。

如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形。最长边所对的角为直角。接下来分享勾股定理逆定理证明方法。

倍角公式是三角函数中非常实用的一类公式。就是把二倍角的三角函数用本角的三角函数表示出来。接下来分享三角函数倍角公式及证明方法。

勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。下面是勾股定理的证明方法和公式,供大家参考。