全等三角形的判定方法

关于三角形的知识点有很多，本篇文章主要介绍全等三角形的五种判定方法，同学们要深刻体会。

三角形全等判定方法：

1.三边对应相等的两个三角形全等，简称SSS（边边边）

举例：在△ABC中，AC=BD，AD=BC，求证∠A=∠B.

证明：在△ACD与△BDC中{AC=BD，AD=BC，CD=CD.

∴△ACD≌△BDC.（SSS）

∴∠A=∠B.（全等三角形的对应角相等）

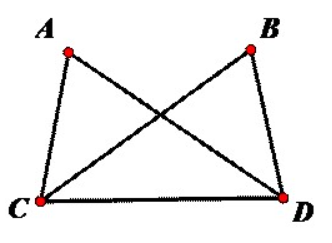
2：三角形的其中两条边对应相等，且两条边的夹角也对应相等的两个三角形全等。简称SAS（边角边）。

举例：如下图，AB平分∠CAD，AC=AD，求证∠C=∠D.证明：∵AB平分∠CAD.∴∠CAB=∠BAD.在△ACB与△ADB中{AC=AD，∠CAB=∠BAD，AB=AB.∴△ACB≌△ADB.（SAS）∴∠C=∠D.（全等三角形的对应角相等）

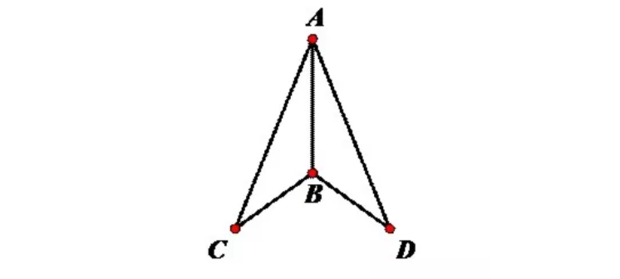
3：三角形的其中两个角对应相等，且两个角夹的的边也对应相等的两个三角形全等。简称ASA（角边角）。

举例：如下图，AB=AC，∠B=∠C，求证△ABE≌△ACD.证明：在△ABE与△ACD中{∠A=∠A，AB=AC，∠B=∠C.∴△ABE≌△ACD.（ASA）

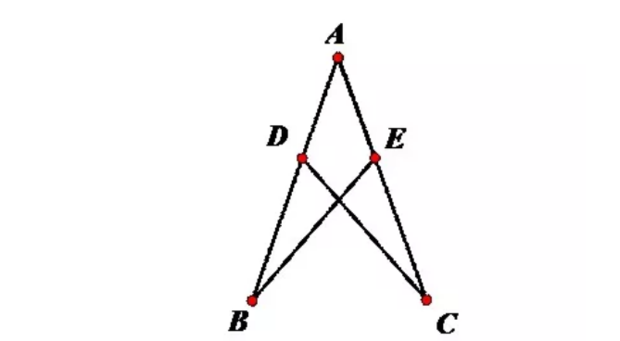
4：三角形的其中两个角对应相等，且对应相等的角所对应的边也对应相等的两个三角形全等。简称AAS（角角边）。

举例：如下图，AB=DE，∠A=∠E，求证∠B=∠D.证明：在△ABC与△EDC中{∠A=∠E，∠ACB=∠DCE，AB=DE.∴△ABC≌△EDC.（AAS）∴∠B=∠D.（全等三角形的对应角相等）

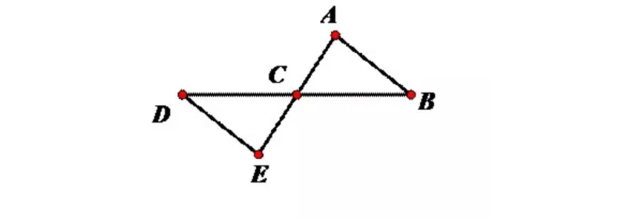
5：在直角三角形中一条斜边和一条直角边对应相等的两个直角三角形全等。简称HL（斜边、直角边）。

定义举例：如下图，Rt△ADC与Rt△BCD，AC=BD，求证AD=BC.

证明：在Rt△ADC与Rt△BCD中{AC=BD，CD=CD.∴Rt△ADC与Rt△BCD.（HL）∴AD=BC.（全等三角形的对应边相等）

相关概念及性质

能够完全重合的两个三角形叫做全等三角形，“全等”用符号“≌”表示，读作“全等于”。当两个三角形完全重合时，互相重合的顶点叫做对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角。由此，可以得出：全等三角形的对应边相等，对应角相等。

全等三角形的性质：

1.全等三角形的对应角相等。

2.全等三角形的对应边相等。

3.全等三角形的对应边上的高对应相等。

4.全等三角形的对应角的角平分线相等。

5.全等三角形的对应边上的中线相等。

6.全等三角形面积相等。

7.全等三角形周长相等。

8.全等三角形的对应角的三角函数值相等。

全等三角形八大模型

（1）角平分线模型 

（2）垂直模型   

（3）一线三等角模型 

（4）倍长中线模型 

（5）截长补短法    

（6）手拉手模型 

（7）半角模型           

（8）边边角模型