梯形中位线定理怎么证明

梯形中位线定理是指连接梯形两腰中点的线段。梯形的中位线平行于两底，并且等于两底和的一半。接下来分享梯形中位线定理的证明方法，供参考。

梯形中位线定理证明方法

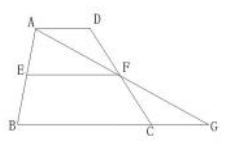
如图，四边形ABCD是梯形，AD∥BC，E、F分别是AB、CD边上的中点，求证：EF∥AD，且EF=(AD+BC)/2

证明：

连接AF并延长交BC的延长线于G。

∵AD∥BC

∴∠ADF=∠GCF

∵F是CD的中点

∴DF=FC

∵∠AFD=∠CFG

∴△ADF≌△GCF(ASA)

∴AF=FG，AD=CG

∴F是AG的中点

∵E是AB的中点

∴EF是△ABG的中位线

∴EF∥BG,EF=BG/2=(BC+CG)/2

∴EF=(AD+BC)/2

∵AD∥BC

∴EF∥AD∥BC

梯形中位线定理

连接梯形两腰中点的线段叫做梯形的中位线，梯形的中位线平行于两底，并且等于两底和的一半。

梯形的中位线L平行于底边，且其长度为上底加下底和的一半，用符号表示是：L=(a+b)/2。

中位线在关于梯形的各种题型中都是一条得天独厚的辅助线。

梯形的计算公式

1、梯形的周长公式：上底+下底+腰+腰，用字母表示：L=a+b+c+d。

2、等腰梯形的周长公式：上底+下底+2腰，用字母表示：a+c+2b。

3、梯形的面积公式：（上底+下底）×高÷2，用字母表示：S=（a+c）×h÷2。

4、对角线互相垂直的梯形面积为：对角线×对角线÷2。