秘密★启用前 试卷类型:A
二〇一八年东营市初中学业水平考试
数 学 试 题
(总分120分 考试时间120分钟)
注意事项:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷为选择题,30分;第Ⅱ卷为非选择题,90分;本试题共6页.
2.数学试题答题卡共8页.答题前,考生务必将自己的姓名、准考证号、座号等填写在试题和答题卡上,考试结束,试题和答题卡一并收回.
3.第Ⅰ卷每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑.如需改动,先用橡皮擦干净,再改涂其它答案.第Ⅱ卷按要求用0.5mm碳素笔答在答题卡的相应位置上.
第Ⅰ卷(选择题 共30分)
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1.![]() 的倒数是( )
的倒数是( )
A.![]() B.5 C.
B.5 C. ![]() D.
D.![]()
2.下列运算正确的是( )
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
![]()
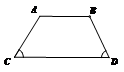
 3.下列图形中,根据AB∥CD,能得到∠1=∠2的是( )
3.下列图形中,根据AB∥CD,能得到∠1=∠2的是( )
![]()
![]()
![]()


![]()
![]()
![]()
![]()
A B C D
4.在平面直角坐标系中,若点P(![]() ,
,![]() )在第二象限,则
)在第二象限,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
5.为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A.众数是100 B.中位数是30 C.极差是20 D.平均数是30
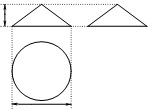
6.小岩打算购买气球装扮学校“毕业典礼”活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )
 A.19 B.18 C.16 D.15
A.19 B.18 C.16 D.15



![]()
![]()
![]()


7.如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( )
A. AD=BC B. CD=BF C. ∠A=∠C D. ∠F=∠CDF
8.如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
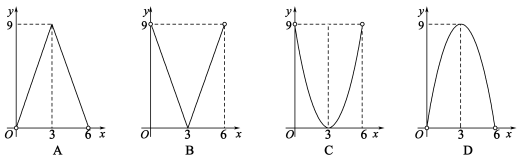
![]() 9.如图所示,已知△ABC中,BC=12,BC边上的高h=6,D为BC上一点,EF∥BC,交AB于点E,交AC于点F,设点E到边BC的距离为x.则△DEF的面积y关于x的函数图象大致为 ( )
9.如图所示,已知△ABC中,BC=12,BC边上的高h=6,D为BC上一点,EF∥BC,交AB于点E,交AC于点F,设点E到边BC的距离为x.则△DEF的面积y关于x的函数图象大致为 ( )
10.如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①![]() ;②∠ABD+∠ECB=45°;③BD⊥CE;④
;②∠ABD+∠ECB=45°;③BD⊥CE;④![]() .
.
其中正确的是( )
A. ①②③④ B. ②④ C. ①②③ D. ①③④

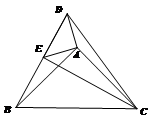
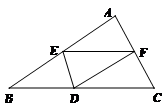



第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分.只要求填写最后结果.
11.东营市大力推动新旧动能转换,产业转型升级迈出新步伐.建立了新旧动能转换项目库,筛选论证项目377个,计划总投资4147亿元.4147亿元用科学记数法表示为 元.
12. 分解因式:![]() = .
= .
13. 有五张背面完全相同的卡片,其正面分别画有等腰三角形、平行四边形、矩形、正方形、菱形,将这五张卡片背面朝上洗匀,从中随机抽取一张,卡片上的图形是中心对称图形的概率是 .
14.如图,B(3,-3),C(5,0),以OC ,CB为边作平行四边形OABC,则经过点A的反比例函数的解析式为 .
15.如图,在Rt△ABC中,∠B=90°,以顶点C为圆心,适当长为半径画弧,分别交AC,BC于点E,F,再分别以点E,F为圆心,大于![]() EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D,若BD=3,AC=10,则△ACD的面积是 .
EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D,若BD=3,AC=10,则△ACD的面积是 .
![]()


![]()
![]()
![]()
![]()
16.已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积为 .
17.在平面直角坐标系内有两点A、B,其坐标为A![]() ,B(2,7),点M为x轴上的一个动点,若要使
,B(2,7),点M为x轴上的一个动点,若要使![]() 的值最大,则点M的坐标为 .
的值最大,则点M的坐标为 .
18.如图,在平面直角坐标系中,点![]() ,
,![]() ,
,![]() ,…和
,…和![]() ,
,![]() ,
,![]() ,…分别在直线
,…分别在直线![]() 和
和![]() 轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果点
轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果点![]() (1,1),那么点
(1,1),那么点![]() 的纵坐标是 .
的纵坐标是 .
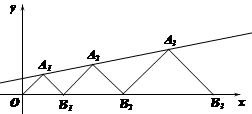
![]()
![]()
三、解答题:本大题共7小题,共62分.解答要写出必要的文字说明、证明过程或演算步骤.
19. (本题满分7分,第⑴题4分,第⑵题3分)
(1)计算:![]() ;
;
(2)解不等式组:
![]() 并判断-1,
并判断-1,![]() 这两个数是否为该不等式组的解.
这两个数是否为该不等式组的解.
20.(本题满分8分)
2018年东营市教育局在全市中小学开展了“情系疏勒 书香援疆”捐书活动,200多所学校的师生踊跃参与,向新疆疏勒县中小学共捐赠爱心图书28.5万余本.某学校学生社团对本校九年级学生所捐图书进行统计,根据收集的数据绘制了下面不完整的统计图表.请你根据统计图表中所提供的信息解答下列问题:

图书种类 | 频数(本) | 频率 |
名人传记 | 175 | a |
科普图书 | b | 0.30 |
小说 | 110 | c |
其他 | 65 | d |
![]()
![]()
(1)求该校九年级共捐书多少本;
(2)统计表中的a= ,b= ,c= ,d= ;
(3)若该校共捐书1500本,请估计“科普图书”和“小说”一共多少本;
(4)该社团3名成员各捐书1本,分别是1本“名人传记”,1本“科普图书”,1本“小说”,要从这3人中任选2人为受赠者写一份自己所捐图书的简介,请用列表法或树状图求选出的2人恰好1人捐“名人传记”,1人捐“科普图书”的概率.
21.(本题满分8分)
小明和小刚相约周末到雪莲大剧院看演出,他们的家分别距离剧院1200m和2000m,两人分别从家中同时出发,已知小明和小刚的速度比是3:4,结果小明比小刚提前4min到达剧院.求两人的速度.
22.(本题满分8分)
如图,CD是⊙O的切线,点C在直径AB的延长线上.
(1)求证:∠CAD=∠BDC;
(2)若BD=![]() AD,AC=3,求CD的长.
AD,AC=3,求CD的长.

![]()
23.(本题满分9分)
关于![]() 的方程
的方程![]() 有两个相等的实数根,其中∠A是锐角三角形ABC的一个内角.
有两个相等的实数根,其中∠A是锐角三角形ABC的一个内角.
(1)求sinA的值;
(2)若关于y的方程![]() 的两个根恰好是△ABC的两边长,求△ABC的周长.
的两个根恰好是△ABC的两边长,求△ABC的周长.
24.(本题满分10分)
(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=![]() ,BO:CO=1:3,求AB的长.
,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,
AO=![]() ,
,
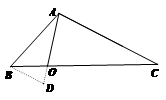 ∠ABC=∠ACB=75°, BO:OD=1:3,求DC的长.
∠ABC=∠ACB=75°, BO:OD=1:3,求DC的长.
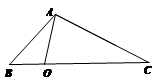
![]()
![]()
![]()
25.(本题满分12分)
如图,抛物线y=a![]() (a
(a![]() 0)与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC.
0)与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC.
(1)求线段OC的长度;
(2)设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式;
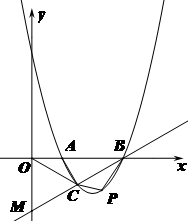 (3)在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
秘密★启用前 试卷类型:A
数学试题参考答案及评分标准
评卷说明:
1. 选择题和填空题中的每小题,只有满分和零分两个评分档,不给中间分.
2. 解答题中的每小题的解答中所对应的分数,是指考生正确解答到该步骤所应得的累计分数.本答案对每小题只给出一种解法,对考生的其他解法,请参照评分标准相应评分.
3. 如果考生在解答的中间过程出现计算错误,但并没有改变试题的实质和难度,其后续部分酌情给分,但最多不超过正确解答分数的一半;若出现严重的逻辑错误,后续部分就不再给分.
一.选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,共30分.选错、不选或选出的答案超过一个均记零分.
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | A | D | B | C | B | B | D | C | D | A |
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题4分,共28分.只要求填写最后结果.
11.![]() ; 12.
; 12. ![]() ; 13.
; 13. ![]() ; 14.
; 14. ![]() ;
;
15. 15; 16. ![]() ; 17.
; 17. ![]() ; 18.
; 18. ![]() .
.
三、解答题:本大题共7小题,共62分.解答要写出必要的文字说明、证明过程或演算步骤.
19.(本题满分7分,第(1)题4分,第(2)题3分)
解:(1)原式=![]() …………………3分
…………………3分
=![]() ……………………………………………4分
……………………………………………4分
(2) 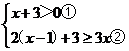
解不等式①得:x>-3,解不等式②得:x≤1………………………………………1分
所以不等式组的解集为: -3<x≤1. …………………………………………………2分
则-1是不等式组的解,![]() 不是不等式组的解.…………………………………………3分
不是不等式组的解.…………………………………………3分
20.(本题满分8分)
解:(1)该校九年级共捐书:![]() ……………………………………1分
……………………………………1分
(2)a=0.35………………………………………………………………………………1.5分
b=150…………………………………………………………………………………2分
c=0.22………………………………………………………………………………2.5分
d=0.13…………………………………………………………………………………3分
(3)![]() (本)…………………………………………………5分
(本)…………………………………………………5分
(4)分别用“1、2、3”代表“名人传记”、“科普图书”、“小说”三本书,可用列表法表示如下:
| 1 | 2 | 3 |
1 |
| (2,1) | (3,1) |
2 | (1,2) |
| (3,2) |
3 | (1,3) | (2,3) |
|
则所有等可能的情况有6种,其中2人恰好1人捐“名人传记”,1人捐“科普图书”的情况有2种.…………………………………………………………………… …………7分
所以所求的概率:![]() ………………………………………………………8分
………………………………………………………8分
21.(本题满分8分)
解:设小明和小刚的速度分别是3x米/分和4 x米/分…………………………………1分
则![]() …………………………………………………………………3分
…………………………………………………………………3分
解得 x=25………………………………………………………………………………5分
检验:当x=25时,3x≠0,4 x≠0
所以分式方程的解为x=25……………………………………………………………6分
则3x=75 4x=100………………………………………………………………………7分
答:小明的速度是75米/分,小刚的速度是100米/分.………………………………8分
 22.(本题满分8分)
22.(本题满分8分)
(1)证明:连接OD
∵OB=OD
∴∠OBD=∠ODB…………………………1分
∵CD是⊙O的切线,OD是⊙O的半径
∴∠ODB+∠BDC=90°……………………2分
 ∵AB是⊙O的直径
∵AB是⊙O的直径
∴∠ADB=90°
∴∠OBD +∠CAD = 90°………………………………………3分
∴∠CAD=∠BDC………………………………………………4分
(2)解:∵∠C=∠C,∠CAD=∠BDC
∴△CDB ∽ △CAD………………………………………………5分
∴![]() …………………………………………………6分
…………………………………………………6分![]()
∵![]()
∴![]() …………………………………………………7分
…………………………………………………7分
∵ AC=3
∴ CD=2…………………………………………………8分
23. (本题满分9分)
解:(1)因为关于x的方程![]() 有两个相等的实数根,
有两个相等的实数根,
则△=25sin2A-16=0………………………………………1分
∴sin2A=![]() ,
,
∴sinA=![]() ,……………………………………………2分
,……………………………………………2分
∵∠A为锐角,
∴sinA=![]() ;………………………………………………3分
;………………………………………………3分
(2)由题意知,方程y2﹣10y+k2-4k+29=0有两个实数根,
则△≥0,………………………………………………4分
∴100﹣4(k2-4k+29)≥0,
∴﹣(k-2)2≥0,
∴(k-2)2≤0,
又∵(k-2)2≥0,
∴k=2.…………………………………………………5分
把k=2代入方程,得y2﹣10y+25=0,
解得y1=y2=5,
 ∴△ABC是等腰三角形,且腰长为5. …………6分
∴△ABC是等腰三角形,且腰长为5. …………6分
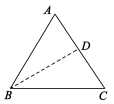
分两种情况:
①  ∠A是顶角时:如图,过点B作BD⊥AC于点D, 在Rt△ABD中,AB=AC=5
∠A是顶角时:如图,过点B作BD⊥AC于点D, 在Rt△ABD中,AB=AC=5
∵sinA=![]() , ∴AD=3 ,BD=4∴DC=2, ∴BC=
, ∴AD=3 ,BD=4∴DC=2, ∴BC=![]() .
.
∴△ABC的周长为![]() . ……………………………7分
. ……………………………7分
② 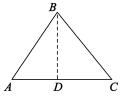 ∠A是底角时:如图,过点B作BD⊥AC于点D, 在Rt△ABD中,AB=5 ∵sinA=
∠A是底角时:如图,过点B作BD⊥AC于点D, 在Rt△ABD中,AB=5 ∵sinA=![]() , ∴A D =DC =3, ∴AC=6.
, ∴A D =DC =3, ∴AC=6.
 ∴△ABC的周长为16. …………………………8分
∴△ABC的周长为16. …………………………8分
综合以上讨论可知:△ABC的周长为![]() 或16……………9分
或16……………9分
24.(本题满分10分)
(1)75,……………………………………………1分
(2)解:过点B作BE∥AD交AC于点E
∵AC⊥AD
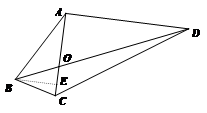 ∴∠DAC =∠BEA=90°
∴∠DAC =∠BEA=90°
∵∠AOD =∠EOB
∴△AOD∽△EOB……………………………………………3分
∴![]()
 ∵BO:OD=1:3
∵BO:OD=1:3
∴![]() ……………………………………………4分
……………………………………………4分
∵AO=![]()
∴EO=![]()
∴AE=![]() ……………………………………………5分
……………………………………………5分
∵∠ABC=∠ACB=75°
∴∠BAC=30°,AB=AC……………………………………………6分
∴AB=2BE
在Rt△AEB中,![]()
即![]() ,得BE=4……………………………………………7分
,得BE=4……………………………………………7分
∴AB=AC=8,AD=12……………………………………………8分
在Rt△CAD中,![]()
即![]() ,得CD=
,得CD=![]() …………………………………………10分
…………………………………………10分
25.(本题满分12分)
解:(1)由题可知当y=0时,a![]() =0
=0
解得:x1=1,x2=3
则A(1,0),B(3,0)于是OA=1,OB=3
∵△OCA∽△OBC ∴OC∶OB=OA∶OC …………………2分
∴OC2=OA•OB=3即OC=![]() ……………………………3分
……………………………3分
(2)因为C是BM的中点
∴OC=BC从而点C的横坐标为![]()
又OC=![]() ,点C在x轴下方∴C
,点C在x轴下方∴C![]() …………………5分
…………………5分
设直线BM的解析式为y=kx+b,

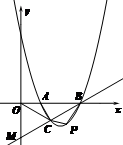 因其过点B(3,0),C
因其过点B(3,0),C![]() ,
,
则有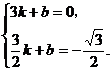
∴![]() ,
,![]()
∴![]() ……………………5分
……………………5分
又点C![]() 在抛物线上,代入抛物线解析式,
在抛物线上,代入抛物线解析式,
解得a=![]() ……………………6分
……………………6分
∴抛物线解析式为:![]() ……………………7分
……………………7分
(3)点P存在.……………………8分
设点P坐标为(x,![]() ),过点P作PQ
),过点P作PQ![]() x轴交直线BM于点Q,
x轴交直线BM于点Q,
则Q(x,![]() ),
),
PQ=![]() ……………………9分
……………………9分
当△BCP面积最大时,四边形ABPC的面积最大
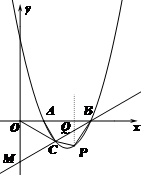
![]()
![]()
![]()
![]() ……………………10分
……………………10分
 当
当![]() 时,
时,![]() 有最大值,四边形ABPC的面积最大,…11分
有最大值,四边形ABPC的面积最大,…11分
此时点P的坐标为![]()
![]() ……………………12分
……………………12分
![]()

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...