2018年舟山中考数学试卷真题【word版含答案】
为了方便阅读请点击全屏查看
卷Ⅰ(选择题)
一、选择题(本题有10小题,每题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
1.下列几何体中,俯视图为三角形的是( )

A. B. C. D.
2.2018年5月25日,中国探月工程的“鹊桥号”中继星成功运行于地月拉格朗日![]() 点,它距离地球约
点,它距离地球约![]() .数1500000用科学记数法表示为( )
.数1500000用科学记数法表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.2018年1~4月我国新能源乘用车的月销售情况如图所示,则下列说法错误的是( )
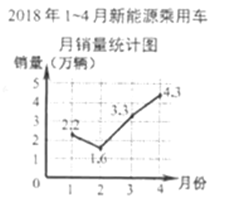
A.1月份销售为2.2万辆
B.从2月到3月的月销售增长最快
C.4月份销售比3月份增加了1万辆
D.1~4月新能源乘用车销售逐月增加
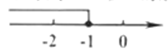
4.不等式![]() 的解在数轴上表示正确的是( )
的解在数轴上表示正确的是( )
![]()
![]()
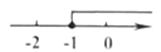
A. B. C. D.
5.将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )
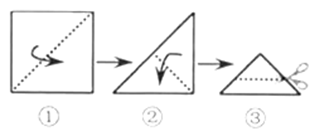
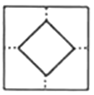
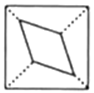
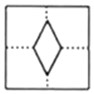
A. B. C. D.
6.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是( )
A.点在圆内 B.点在圆上 C.点在圆心上 D.点在圆上或圆内
7.欧几里得的《原本》记载,形如![]() 的方程的图解法是:画
的方程的图解法是:画![]() ,使
,使![]() ,
,![]() ,
,![]() ,再在斜边
,再在斜边![]() 上截取
上截取![]() .则该方程的一个正根是( )
.则该方程的一个正根是( )
A.![]() 的长 B.
的长 B.![]() 的长 C.
的长 C.![]() 的长 D.
的长 D.![]() 的长
的长
8.用尺规在一个平行四边形内作菱形![]() ,下列作法中错误的是( )
,下列作法中错误的是( )

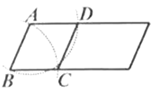
A. B. C. D.
9.如图,点![]() 在反比例函数
在反比例函数![]() 的图象上,过点
的图象上,过点![]() 的直线与
的直线与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,且
,且![]() ,
,![]() 的面积为1,则
的面积为1,则![]() 的值为( )
的值为( )
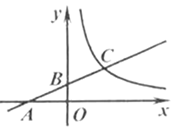
A.1 B.2 C.3 D.4
10.某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是( )
A.甲 B.甲与丁 C.丙 D.丙与丁
卷Ⅱ(非选择题)
二、填空题(本题有6小题,每题4分,共24分)
11.分解因式:![]() .
.
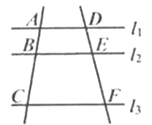
12.如图,直线![]() ,直线
,直线![]() 交
交![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ;直线
;直线![]() 交
交![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() .已知
.已知![]() ,则
,则![]() .
.
13.小明和小红玩抛硬币游戏,连续抛两次.小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我赢.”小红赢的概率是 ,据此判断该游戏 (填“公平”或“不公平”).
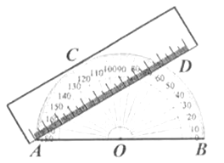
14.如图,量角器的0度刻度线为![]() ,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点
,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点![]() ,直尺另一边交量角器于点
,直尺另一边交量角器于点![]() ,
,![]() ,量得
,量得![]() ,点
,点![]() 在量角器上的读数为
在量角器上的读数为![]() ,则该直尺的宽度为____________
,则该直尺的宽度为____________![]() .
.
15.甲、乙两个机器人检测零件,甲比乙每小时多检测20个,甲检测300个比乙检测200个所用的时间少![]() ,若设甲每小时检测
,若设甲每小时检测![]() 个,则根据题意,可列出方程: .
个,则根据题意,可列出方程: .
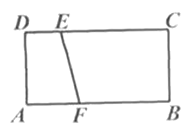
16.如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 在边
在边![]() 上一动点,以
上一动点,以![]() 为斜边作
为斜边作![]() .若点
.若点![]() 在矩形
在矩形![]() 的边上,且这样的直角三角形恰好有两个,则
的边上,且这样的直角三角形恰好有两个,则![]() 的值是 .
的值是 .
三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分,第22,23题每题10分,第24题12分,共66分)
17.(1)计算:![]() ;
;
(2)化简并求值:![]() ,其中
,其中![]() ,
,![]() .
.
18.用消元法解方程组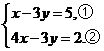 时,两位同学的解法如下:
时,两位同学的解法如下:
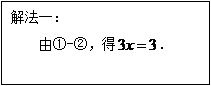
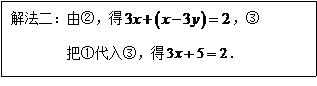
(1)反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“×”.
(2)请选择一种你喜欢的方法,完成解答.
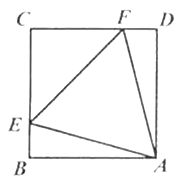
19.如图,等边![]() 的顶点
的顶点![]() ,
,![]() 在矩形
在矩形![]() 的边
的边![]() ,
,![]() 上,且
上,且![]() .
.
求证:矩形![]() 是正方形.
是正方形.
20.某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为![]() 的产品为合格),随机各抽取了20个样品进行检测,过程如下:
的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据(单位:![]() ):
):
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
|
|
|
|
|
|
|
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 | 1 | 2 |
|
| 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
应用数据:
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
21.小红帮弟弟荡秋千(如图1),秋千离地面的高度![]() 与摆动时间
与摆动时间![]() 之间的关系如图2所示.
之间的关系如图2所示.

(1)根据函数的定义,请判断变量![]() 是否为关于
是否为关于![]() 的函数?
的函数?
(2)结合图象回答:
①当![]() 时,
时,![]() 的值是多少?并说明它的实际意义.
的值是多少?并说明它的实际意义.
②秋千摆动第一个来回需多少时间?
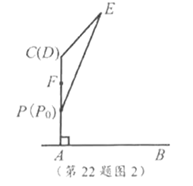
22.如图1,滑动调节式遮阳伞的立柱![]() 垂直于地面
垂直于地面![]() ,
,![]() 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,
,![]() .当点
.当点![]() 位于初始位置
位于初始位置![]() 时,点
时,点![]() 与
与![]() 重合(图2).根据生活经验,当太阳光线与
重合(图2).根据生活经验,当太阳光线与![]() 垂直时,遮阳效果最佳.
垂直时,遮阳效果最佳.
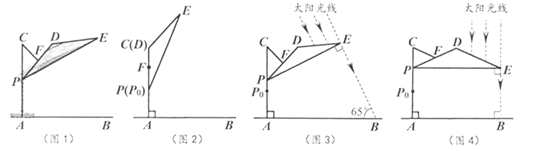
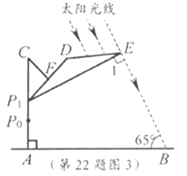
(1)上午10:00时,太阳光线与地面的夹角为![]() (图3),为使遮阳效果最佳,点
(图3),为使遮阳效果最佳,点![]() 需从
需从![]() 上调多少距离?(结果精确到
上调多少距离?(结果精确到![]() )
)
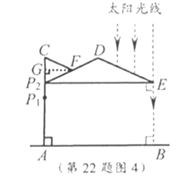
(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点![]() 在(1)的基础上还需上调多少距离?(结果精确到
在(1)的基础上还需上调多少距离?(结果精确到![]() )
)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
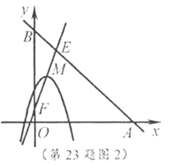
23.已知,点![]() 为二次函数
为二次函数![]() 图象的顶点,直线
图象的顶点,直线![]() 分别交
分别交![]() 轴正半轴,
轴正半轴,![]() 轴于点
轴于点![]() ,
,![]() .
.

(1)判断顶点![]() 是否在直线
是否在直线![]() 上,并说明理由.
上,并说明理由.
(2)如图1,若二次函数图象也经过点![]() ,
,![]() ,且
,且![]() ,根据图象,写出
,根据图象,写出![]() 的取值范围.
的取值范围.
(3)如图2,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 内,若点
内,若点![]() ,
,![]() 都在二次函数图象上,试比较
都在二次函数图象上,试比较![]() 与
与![]() 的大小.
的大小.
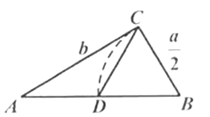
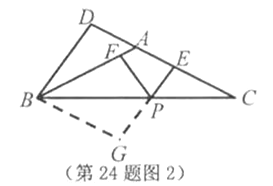
24.已知,![]() 中,
中,![]() ,
,![]() 是
是![]() 边上一点,作
边上一点,作![]() ,分别交边
,分别交边![]() ,
,![]() 于点
于点![]() ,
,![]() .
.

(1)若![]() (如图1),求证:
(如图1),求证:![]() .
.
(2)若![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() (或
(或![]() 的延长线)于点
的延长线)于点![]() .试猜想:线段
.试猜想:线段![]() ,
,![]() 和
和![]() 之间的数量关系,并就
之间的数量关系,并就![]() 情形(如图2)说明理由.
情形(如图2)说明理由.
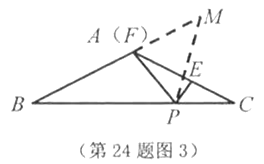
(3)若点![]() 与
与![]() 重合(如图3),
重合(如图3),![]() ,且
,且![]() .
.
①求![]() 的度数;
的度数;
②设![]() ,
,![]() ,
,![]() ,试证明:
,试证明:![]() .
.
2018年舟山中考数学试卷真题数学参考答案
一、选择题
1-5: CBDAA 6-10: DBCDB
二、填空题
11. ![]() 12. 2 13.
12. 2 13. ![]() ;不公平
;不公平
14. ![]() 15.
15. ![]() 16. 0或
16. 0或![]() 或4
或4
三、解答题
17.(1)原式![]() .
.
(2)原式![]() .
.
当![]() ,
,![]() 时,原式
时,原式![]() .
.
18.(1)解法一中的计算有误(标记略).
(2)由①-②,得![]() ,解得
,解得![]() ,
,
把![]() 代入①,得
代入①,得![]() ,解得
,解得![]() ,
,
所以原方程组的解是![]() .
.
18.用消元法解方程组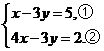 时,两位同学的解法如下:
时,两位同学的解法如下:
19.(方法一)∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴矩形![]() 是正方形.
是正方形.
(方法二)(连结![]() ,利用轴对称证明,表述正确也可)
,利用轴对称证明,表述正确也可)

20.(1)甲车间样品的合格率为![]() .
.
(2)∵乙车间样品的合格产品数为![]() (个),
(个),
∴乙车间样品的合格率为![]() .
.
∴乙车间的合格产品数为![]() (个).
(个).
(3)①从样品合格率看,乙车间合格率比甲车间高,所以乙车间生产的新产品更好.
②从样品的方差看,甲、乙平均数相等,且均在合格范围内,而乙的方差小于甲的方差,说明乙比甲稳定,所以乙车间生产的新产品更好.
21.(1)∵对于每一个摆动时间![]() ,都有一个唯一的
,都有一个唯一的![]() 的值与其对应,
的值与其对应,
∴变量![]() 是关于
是关于![]() 的函数.
的函数.
(2)①![]() ,它的实际意义是秋千摆动
,它的实际意义是秋千摆动![]() 时,离地面的高度为
时,离地面的高度为![]() .
.
②![]() .
.
22.(1)如图2,当点![]() 位于初始位置
位于初始位置![]() 时,
时,![]() .
.
如图3,10:00时,太阳光线与地面的夹角为![]() ,点
,点![]() 上调至
上调至![]() 处,
处,
![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() 为等腰直角三角形,∴
为等腰直角三角形,∴![]() ,
,
∴![]() ,
,
即点![]() 需从
需从![]() 上调
上调![]() .
.
(2)如图4,中午12:00时,太阳光线与![]() ,地面都垂直,点
,地面都垂直,点![]() 上调至
上调至![]() 处,
处,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,得
,得![]() 为等腰三角形,
为等腰三角形,
∴![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即点![]() 在(1)的基础上还需上调
在(1)的基础上还需上调![]() .
.
23.(1)∵点![]() 坐标是
坐标是![]() ,
,
∴把![]() 代入
代入![]() ,得
,得![]() ,
,
∴点![]() 在直线
在直线![]() 上.
上.
(2)如图1,∵直线![]() 与
与![]() 轴交于点为
轴交于点为![]() ,∴点
,∴点![]() 坐标为
坐标为![]() .
.
又∵![]() 在抛物线上,
在抛物线上,
∴![]() ,解得
,解得![]() ,
,
∴二次函数的表达式为![]() ,
,
∴当![]() 时,得
时,得![]() ,
,![]() ,∴
,∴![]() .
.
观察图象可得,当![]() 时,
时,
![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.

(3)如图2,∵直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
而直线![]() 表达式为
表达式为![]() ,
,
解方程组![]() ,得
,得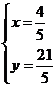 .∴点
.∴点![]() ,
,![]() .
.
∵点![]() 在
在![]() 内,
内,
∴![]() .
.
当点![]() ,
,![]() 关于抛物线对称轴(直线
关于抛物线对称轴(直线![]() )对称时,
)对称时,
![]() ,∴
,∴![]() .
.
且二次函数图象的开口向下,顶点![]() 在直线
在直线![]() 上,
上,
综上:①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ;
;
③当![]() 时,
时,![]() .
.
24.(1)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.

(2)猜想:![]() ,理由如下:
,理由如下:
过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
(3)①设![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() .
.
②延长![]() 至
至![]() ,使
,使![]() ,连结
,连结![]() ,
,
∵![]() ,
,![]() .
.
∴![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .∵
.∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.







孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...