2018年承德中考数学冲刺试卷【精选word版 可下载】

2018年承德中考数学冲刺试卷【精选word版 可下载】

由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！

一．选择题（共12小题，满分36分）

1．（3分）下列算式中,结果等于a6的是【  】

A.  a2•a3    B.a2+ a2+ a2   C. a4+ a2    D. a2• a2• a2 

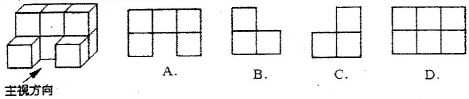
2．（3分）如图是用八块相同的小正方体搭建的几何体,它的左视图是（  ）

3．（3分）据福布斯2017年9月19的最新数据显示，恒大集团董事局主席许家印以391亿美元的身价成中国新首富，略高于马化腾和马云．391亿用科学记数法表示为（　　）

A．3.91×108              B．3.91×109              C．3.91×1010              D．3.91×1011

4．（3分）不等式﹣x+2≥0的解集在数轴上表示正确的是（　　）

A．              B．             

C．              D．

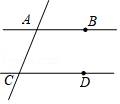
5．（3分）如图，已知直线AB、CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB、CD、AC上），设∠BAE=α，∠DCE=β．下列各式：①α+β，②α﹣β，③β﹣α，④360°﹣α﹣β，∠AEC的度数可能是（　　）

A．①②③              B．①②④              C．①③④              D．①②③④

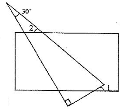
6．（3分）直角三角板和直尺如图放置,若∠1=40°,则∠2的度数为（  ）

A.30°      B.20°    C.40°      D.50°

7．（3分）关于x的一元二次方程ax2+3x﹣2=0有两个不相等的实数根，则a的值可以是（　　）

A．0              B．﹣1              C．﹣2              D．﹣3

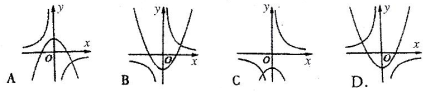
8．（3分）已知m≠0,函数y=-mx2十n与y=在同一直角坐标系中的大致图像可能（   ）

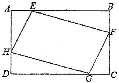
9．（3分）如图,矩形ABCD中,AB=8,BC=6,点E、F、G、H分别在矩形ABCD各边上,且

AE=CG,BF=DH,则四边形EFCH周长的最小值为（   ）

A,10   B.4   C.20    D.8

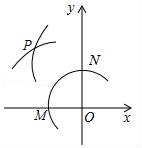
10．（3分）如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧在第二象限交于点P．若点P的坐标为（2a，b+1），则a与b的数量关系为（　　）

A．a=b              B．2a﹣b=1              C．2a+b=﹣1              D．2a+b=1

11．（2分）A种饮料比B种饮料单价少1元，小峰买了2瓶A种饮料和3瓶B种饮料，一共花了13元，如果设B种饮料单价为x元/瓶，那么下面所列方程正确的是（　　）

A．2x+3（x+1）=13                         B．2（x+1）+3x=13             

C．2（x﹣1）+3x=13                      D．2x+3（x﹣1）=13

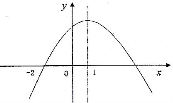
12．（2分）二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-2,0),对称轴为直线x=1,

下列结论:①abc<0;②2a-b=0③b2-4ac>0:;④无论m为何值时,总有am2+bm≤a+b:

⑤9a+c>3b。其中正确的结论序号为（   ）

A.①②③      B.①③④       C.①③④⑤       D.②③④

二．填空题（共6小题，满分18分）

13．（3分）﹣的相反数是　   　，倒数是　   　，绝对值是　   　

14．（3分）已知a、b为有理数，m、n分别表示的整数部分和小数部分，且amn+bn2=4，则2a+b=　   　．

15．（3分）.己知关于x的一元二次方程kx2-5x+3=0有两个不相等的实数根,

则k的取值范围是       

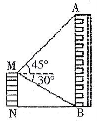
16．（3分）如图,楼房MN与楼房AB相距为30m,在M处测得楼房AB

顶部点A的仰角为45°,底部点B的俯角为30°,则楼房

AB的高度               m,

17．（3分）线段AB的长为5，点A在平面直角坐标系中的坐标为（3，﹣2），点B的坐标为（3，x），则点B的坐标为　   　．

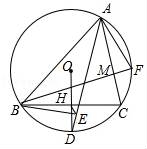
18．（3分）如图，△ABC内接于⊙O，D是弧BC的中点，OD交BC于点H，且OH=DH，连接AD，过点B作BE⊥AD于点E，连接EH，BF⊥AC于M，若AC=5，EH=，则AF=　   　．

三．解答题（共8小题，满分66分）

19．（8分）(1)计算

(2)先化简,再求值其中x的值为(1)中计算的结果.

20.已知:如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE-90°,点E在BC边上.

(1)求证:△ACD≌△ABE.

(2)若∠CDE=60°,求∠AEB的度数

21．（9分）从2开始，连续的偶数相加，它们和的情况如下表：

（1）若n=8时，则S的值为　   　．

（2）根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n=　   　．

（3）根据上题的规律求102+104+106+108+…+200的值（要有过程）

22．（9分）为了促进学生全面发展．河南省某地区教育局在全区中小学开展“书法、手球、豫剧进校园”活动今年8月份，该区某校举行了“朝阳沟”演唱比赛、比赛A、B、C，D，E五个等级，该校部分学生参加了学校的比赛，并将比赛结果绘制成如下两幅不完整的统计图，请根据图中信息，解答下列问题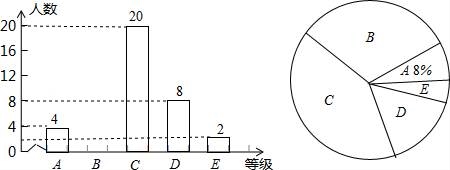

（1）求该校参加本次“朝阳沟”演唱比赛的学生人数；

（2）求扇形统计图B等级所对应扇形的圆心角度数；

（3）已知A等级的4名学生中有2名男生，2名女生，现从中任意选取2名学生作为全校学生的楷模，请你用列表法或画树状图的方法，求出恰好选1男1女的概率．

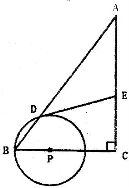
23．（9分）如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,P为边BC上一个动点(可以包括点C但不包括点B),以P为圆心PB为半径作⊙P交AB于点D，过点D作⊙P的切线交边BC于点E.

(1)求证:AE=DE,

(2)若PB=2,求AE的长；

(3)在P点的运动过程中,请直接写出线段AE长度的取值范圄

24．（10分）A、B两辆汽车同时从相距330千米的甲、乙两地相向而行，s（千米）表示汽车与甲地的距离，t（分）表示汽车行驶的时间，如图，L1，L2分别表示两辆汽车的s与t的关系．

（1）L1表示哪辆汽车到甲地的距离与行驶时间的关系？

（2）汽车B的速度是多少？

（3）求L1，L2分别表示的两辆汽车的s与t的关系式．

（4）2小时后，两车相距多少千米？

（5）行驶多长时间后，A、B两车相遇？

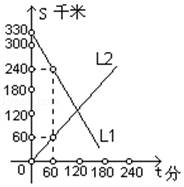
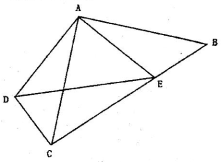
25．（11分）如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．

（1）①猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系，不必证明；

②将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α，得到如图2情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并证明你的判断．

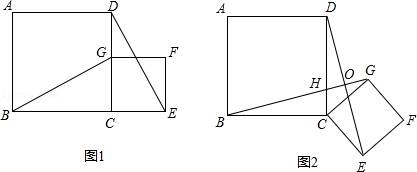
（2）将原题中正方形改为矩形（如图3、4），且AB=a，BC=b，CE=ka，CG=kb （a≠b，k＞0），第（1）题①中得到的结论哪些成立，哪些不成立？若成立，以图4为例简要说明理由．

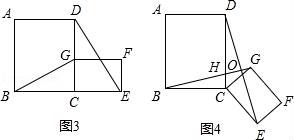
（3）在第（2）题图4中，连接DG、BE，且a=3，b=2，k=，求BE2+DG2的值．

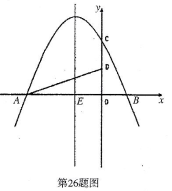
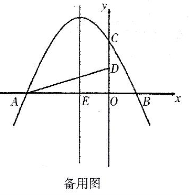
26．（12分）)已知:如图,抛物线yax2+bx+e是由抛物线y= x2的图像向左平移1个单位长度,再向上平移个单位长度得到的.抛物线与x轴交于A、B两点,与y轴交于点C。点D在线段OC上且OD=OB。

(1)写出此抛物线的解析式(化成一般形式)。

(2)求线段AD所在直线的解析式

(3)若点P是第二象限内抛物线上一-点,其横坐标为t,是否存在一点P,使△PAD的面积最大?若存在,求出点P的坐标及△PAD的面积的最大值,若不存在,请说明理由,

(4)若点P仍为为第二象限内抛物线上一点,抛物线的对称轴交x轴于点E,连接PE交AD于点F,当△AEF与△AOD相似时,请直接写出点P的坐标,