![]() 2018广安二中中考数学模拟试题【最新Word版】
2018广安二中中考数学模拟试题【最新Word版】
由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看!
注意事项:
1、本试卷分为试题卷和答题卡,满分100分,考试时间90分钟;
2、在作答前,考生务必将自己的姓名,班级、考场填写在答题卡规定的地方,并认真核对条形码上的姓名和准考证号。考试结束,只交答题卡。
选择题(每题2分,共20分,每小题均有四个选项,其中只有一项符合题目要求)
3 的相反数是( )
A.![]() B.
B.![]() C.3 D.3
C.3 D.3
下列几何体中,正视图是矩形的是()

A B C D
来自全国各地的知名企业家,聚首某市共签约项目投资总额为90900000元,将90900000 用科学计数法表示正确的是()
A.9.09106 B.0.909108 C.9.09107 D.90.9107
下列运算正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
若m![]() 1,则点P(1-m,m)在()
1,则点P(1-m,m)在()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是![]() cm,则这个正六边形的周长是( )
cm,则这个正六边形的周长是( )
A.![]() cm B.12 cm C.
cm B.12 cm C.![]() cm D.36 cm
cm D.36 cm

(第6题图) (第8题图) (第10题图)
7.若不等式![]() 的解集是
的解集是![]() ,则
,则![]() 的取值范围是()
的取值范围是()
a<3 B.a=3 C.a![]() 3 D.a>3
3 D.a>3
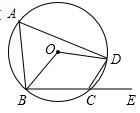
8.如图,四边形ABCD为圆O 的内接四边形,E是BC 延长线上的一点,已知BOD100,
则DCE的度数为( )
70° B.60° C.40° D.50°
9.施工队要铺设一段全长2000米的管道,因在高考期间需停工两天,实际每天施工需比原计划多50米,才能按时完成任务,求原计划每天施工多少米.设原计划每天施工x米,则据题意所列方程正确的是( )
![]() B.
B.![]() C.
C.![]() D.
D.![]()
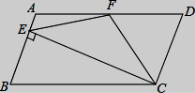
10. 如图,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是______.①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
①② B.②③④ C.①②④ D.①②③④
填空题(每题3分,共18分)
11. 若二次根式![]() 有意义,则x的取值范围是。
有意义,则x的取值范围是。
12.分解因式:2x2-8x+8=。
若关于x的方程![]() 有两个不相等的实数根,则k的取值范围是。
有两个不相等的实数根,则k的取值范围是。
![]() OAB三个顶点坐标分别为O(0,0),A(4,6),B(3,0),以O为位似中心,将
OAB三个顶点坐标分别为O(0,0),A(4,6),B(3,0),以O为位似中心,将![]() OAB缩小为原来的
OAB缩小为原来的![]() ,则A的对应点
,则A的对应点![]() 的坐标为。
的坐标为。
如图,在4×4的方格中(共有16个方格),每个小方格都是边长为1的正方形.O,A,B分别是小正方形的顶点,则扇形OAB的弧长等于________。(结果保留根号及π)
如图,将正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图放置,点A1,A2,A3…和C!,C2,C3…分别在直线y=x+2和x轴上,则点B2017的坐标是。

(第15题图) (第16题图)
三、解答题(共62分,要求写出必要的解答步骤和证明过程)
(5分)计算:![]() +(
+(![]() -2008)
-2008)![]() +
+ ![]() -1 – 6 tan30
-1 – 6 tan30![]()
(5分)先化简![]() ,再求值,其中x为数据4、5、6、5、3、1、2 的众数。
,再求值,其中x为数据4、5、6、5、3、1、2 的众数。
(5分)如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC,BA分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,BC=4.
(1)求点C的坐标和AC所在的直线的解析式.
(2)若反比例函数y=![]() (x>0)的图象经过点B,求反比例函数解析式;
(x>0)的图象经过点B,求反比例函数解析式;
(5分)如图,已知点D在![]() ABC的BC边上,DE‖AC交AB于E,DF‖AB交AC于F。
ABC的BC边上,DE‖AC交AB于E,DF‖AB交AC于F。
求证:AE=DF;
若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由。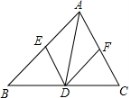
(6分)全面二孩政策定于2016年1月1日正式实施,某中学对七年级部分学生进行了随机问卷调查,其中一个问题“你爸妈如果给你添一个弟弟(或妹妹),你的态度是什么?共有如下四个选项(要求仅选择一个选项):A非常愿意 B 愿意 C 不愿意 D 无所谓,
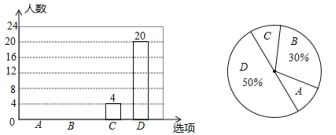
如图是根据调查结果绘制的两幅不完整的统计图,请结合图中信息解答以下问题:
试问本次问卷一共调查了名学生;并补全条形统计图;
若该年级共有600名学生,请你估计全年级可能有多少名学生支持(即态度为“非常愿意”和“愿意”)爸妈给自己添一个弟弟(或妹妹)?
在年级活动课上,老师决定从本次调查回答“非常满意”的同学中随机抽取2名同学来谈谈他们的想法.而本次调查回答“非常愿意”的这些同学只有一名女同学,请用树状图或列表的方法选取两名同学中刚好有这名女同学的概率。
(7分)某公司有甲种原料260Kg,乙种原料270Kg,计划用这两种原料生产A、B两种产品共40件。生产每件A种产品需甲种原料8 Kg,乙种原料5 Kg,可获利润900元;生产每件B种产品需甲种原料
4 Kg,乙种原料9 Kg,可获利润1100元。设安排生产A种产品x件。
完成下表
| 甲(Kg) | 乙(Kg) | 件数(件) |
A |
| 5x | x |
B | 4(40-x) |
| 40-x |
安排生产A、B两种产品的件数有几种方案?试说明理由;
设生产这批40件产品共可获利润y元,将y表示为x的函数,并求出最大利润。
(6分)如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A.B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端AB的距离(结果精确到0.1米,
参考数据:![]() )
)

(6分)根据下列材料,解答问题。
等比数列求和:
概念:对于一列数a1,a2,a3,…,an,…(n为正整数),若从第二个数开始,每一个数与前一个数的比为一定值,即![]() =q(常数),那么这一列数a1,a2,a3,…,an,…成等比数列,这一常数q叫作该数列的公比。
=q(常数),那么这一列数a1,a2,a3,…,an,…成等比数列,这一常数q叫作该数列的公比。
例:求等比数列![]() ,
, ![]() ,
, ![]() ,…,
,…,![]() 的和。
的和。
解:令S =![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ①,则3S = 1+
①,则3S = 1+![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ②
②
由②-①得:2S=1-![]() =
=![]() ,即 S=
,即 S=![]()
(1)模仿例题,求等比数列![]() ,
, ![]() ,
, ![]() ,…,
,…,![]() 的和;
的和;
(2)填空:数列![]() ,
, ![]() ,…,
,…,![]() (a≠1,n为正整数)的公比q=,该数列各项的和为。(写出必要的计算过程)
(a≠1,n为正整数)的公比q=,该数列各项的和为。(写出必要的计算过程)
(8分)如图,AB是⊙O的弦,D是半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于F,且CE=CB。
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
如果CD=15,BE=10,sinA=![]() ,求⊙O的半径。
,求⊙O的半径。
26.(9分)如图,在平面直角坐标系中,顶点为(4,-1)的抛物线交y轴于A点,交x轴与B、C两点(点B在点C的左侧),已知A点的坐标为(0,3)。
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线与点D,如果以点C为圆心的圆与直线BD相切于点E,请判断抛物线的对称轴与圆C有怎样的位置关系,并给出证明;
(3)已知点P是抛物线上的一个动点,且位于A、C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积。

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...