2018长沙市中考数学模拟真题【精编Word版可下载】

2018长沙市中考数学模拟真题【精编Word版可下载】

由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！

注意事项：

1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号；

2.必须在答题卡上答题,在草稿纸、试题卷上答题无效；

3.答题时,请考生注意各大题题号后面的答题提示；

4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁；

5.答题卡上不得使用涂改液、涂改胶和贴纸；

6.本学科试卷共26个小题,考试时量120分钟,满分120分

一、选择题(在下列各题的四个选项中,只有一项是符合题意的,请在答题卡中填涂符合题意的选项,本大题共12个小题,每小题3分,共36分)

1.下列实数中,是无理数的是（  ）

A.0         B.         C.-8             D.

2.下列计算正确的是(    )

A.      B.    C.     D.

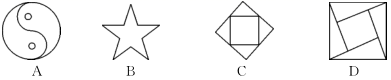
3.下列图形中,是轴对称图形但不是中心对称图形的是（   ）

4.把不等式组的解集表示在数轴上如下图,正确的是（   ）

5.由5个大小小相同的正方体组成的几何体如图所示,从左面看到的图形是（  ）

6.在湖南省第六届网络文化节“学习黑板报”评比活动中,7位评委给某班黑板报的评分情况如下:90,80,90,85,80,90,95,则这组数据的众数和中位数分别为（  ）

A.80,85           B.80,90          C.90,85           D.90,90

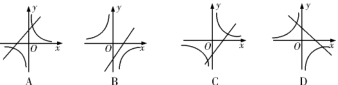
7.若,则一次函数与反比例函数在同一直角坐标系中的图象大致可能是（   ）

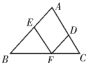
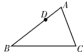
8.如图,在△ABC中,点D、E、F分别是三条边上的点，EF∥AC,DF∥AB,∠B=40°,∠C=55°,则∠EFD=（   ）

      第8题     第9题               第10题

A.65°        B.75°           C.85°          D.95°

9.如图,在△ABC中,BD、CE是△ABC的中线BD与CE相交于点O,点F、G分别是BO、CO

的中点,连接AO.若AO=4cm,BC=6cm,则四边形DEFG的周长是（  ）

A.8cm        B.10cm            C.16cm          D.20cm

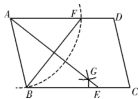
10.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若AE=16,AB=10,则BF的长为（   ）

A.8         B.10               C.12           D.15  

11.为防治雾霾保护环境,某地区掀起“爱绿护绿”热潮,经过两年时间绿地面积增加了44%,则这两年的绿地面积的平均增长率是（   ）

A.10%       B.20%             C.22%           D.44%

12.如图①所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为,已知y与t的函数关系图象如图②(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:①当0＜1≤5时,y=；②tan∠CBE=；③当t=6秒时,△ABE≌△PQB；④当=2秒时,△ABE∽△QBP.其中正确的有（ ）

A.1个            B.2个          C.3个          D.4个

二、填空题(本大题共6个小题,每小题3分,共18分)

13.至2017年底,我国高速公路已达到13.5万公里.四通八达的高速公路网让人们的岀行变得越来越方便,旅行自驾游想去哪里都很快捷。将数据13.5万公里用科学记数法表示为___.

14.分解因式的结果是_______________.

15.分式方程的解是x=_______.

16.如图,小明将边长为2的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形的面积为_______.

       第16题            第17题    第18题

17.在△ABC中,AB=8,AC=6,D是线段AB上的一点，且AD=3,若E是线段AC上的一点,且△ADE与△ABC相似,则AE=________.

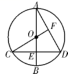
18.如图,已知圆O的弦CD垂直于直径AB,垂足是点E,连接CO并延长交AD于点F,若AB=4,则当CF⊥AD时,DE的长为_______.

三、解答题(本大题共8个小题,共66分)

19.(6分)计算：

20.(6分)先化简,再从-1,0,1,2中选一个合适的数作为x的值代入求值。

21.(8分)学校想知道九年级学生对“党的十九大精神”的了解程度,随机抽取部分九年级学生进行问卷调查,问卷设有4个选项(每位被调查的学生必选且只选一项):A.非常了解.B.了解,C.知道一点D.完全不知道.将调査的结果绘制如下两幅不完整的统计图,请根据两幅统

计图中的信息,解答下列问题：

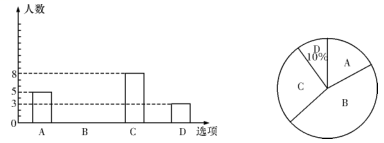
(1)求本次共调查了多少名学生?

(2)补全条形统计图；

(3)该校九年级共有900名学生,请你估计“了解”的学生约有多少名？

(4)在“非常了解”的5人中,有3名男生,2名女生,老师想从这5人中任选两人做宣传员,请用列表或画树状图法求出被选中的两人恰好是一男生一女生的概率。

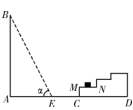
22.(8分)如图所示,巨型广告牌AB背后有一看台CD,台阶每层高0.3米,且AC=17.2米台阶的每一层上都摆了盆栽在晒太阳,设太阳光线与水平地面的夹角为α,当α=60°时,测得广告牌AB在地面上的影长AE=10米(取1.73),

(1)求广告牌AB的高度约为多少米?

(2)过了一会,当ɑ=45°时,问在MN这层的盆栽是否还能晒到太阳?请说明理由。

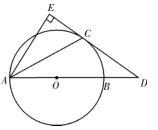
23.(9分)如图,点C是以AB为直径的⊙O上点,D在AB的延长线上,作AE⊥CD于

点E,且AC平分∠BAE》

(1)试判断直线DE与⊙O的位置关系,并说明理由；

(2)若EC=3,sin∠EAC=,求⊙O的半径；

(3)请探索:线段AD、BD、CD之间有何数量关系?并证明你的结论。

24.(9分)近段时间共享单车风靡全国,从而刺激了自行车生产厂家,某厂家准备生产A、B两种型号的共享单车,已知生产6辆A型单车与5辆B型单车的成本相同,生产3辆A型单车与2辆B型单车共需1080元。

(1)求生产一辆A型单车和生产一辆B型单车的成本各为多少元?

(2)由于共享单车公司需求量加大,生产厂家需要再生产A、B两种型号的单车共10000辆,恰逢原料商对基本原料的价格进行调整.调整后,A型单车每辆成本价比原来降低10%,B型单车每辆的成本价不变,如果厂家准备投入的总成本不超过216万元,那么至少要生产多少辆A型单车?

(3)在(2)的条件下,该生产厂家发现,销售过程中每辆A型单车可获利100元,每辆B型单车可获利120元,求全部销售完这批单车获得的利润z与A型单车辆数m之间的函数关系式,并求获利最大的方案以及最大利润。

25.(10分)在平面直角坐标系中,若点P的纵坐标是横坐标的二倍,则称点P为“奋斗点”,例如点(-3,-6),(1,2),(),…都是“奋斗点”.

(1)若点P(m,4)是反比例函数y=(n为常数,n≠0)的图象上的”奋斗点”,求这个反比例函数的解析式；

(2)函数(k为常数,且k≠0)的图象上存在“奋斗点”吗?若存在,请用含k的代数式表示出“奋斗点”的坐标；若不存在,请说明理由；

(3)若二次函数(a,b是常数,a>0)的图象上有且只有一个“奋斗点”,令s=(4-t)b+4a-3,当0≤b≤1时,试求s的最小值.(用含t的代数式表示)

26.(10分)如图,抛物线(a≠0)与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3),顶点为D.

(1)求抛物线的解析式及顶点D的坐标；

(2)连接BC，与抛物线的对称轴交于点E,点P为线段BC上的一个动点(且点P与点B、C、E不重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m，

①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?

②设△BCF的面积为S,求S与m的函数关系式；

(3)若⊙M为△BCD的外接圆,求圆心M的坐标。