![]() 2018年上海中考数学压轴试卷【精选word版】
2018年上海中考数学压轴试卷【精选word版】
由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看!
一、选择题(本大题共6题,每题4分,满分24分)
1、点![]() 和⊙
和⊙![]() 都在同一平面内,⊙
都在同一平面内,⊙![]() 的半径是3,
的半径是3,![]() ,则点
,则点![]() 与⊙
与⊙![]() 的位置是( )
的位置是( )
2、直角三角形的两条直角边的长分别是3和4,则这个直角三角形外接圆的半径是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、如图,某中学绘制了学生选择棋类、武术、摄影、航模四门校本课程情况的扇形统计图,从该图中可以看出选择航模的学生占( )

A、18%
B、17%
C、16%
D、15%
4、如果两圆的半径分别为2和3,圆心距为6,那么这两个圆的位置关系是( )
A、外离 B、相交 C、外切 D、内切
5、下列说法不正确的是( )
A、不在同一直线上的三点确定一个圆
B、平分弧的直径垂直平分弧所对的弦
C、平分弦的直径垂直于弦
D、在同圆中,如果两条弦所对的圆心角相等,那么两条弦所对的弧也相等
6、下列正多边形中,中心角等于内角的是( )
A、正六边形 B、正五边形 C、正四边形 D、正三边形
二、填空题(本大题共12题,每题4分,满分48分)
7、已知圆的半径长为![]() ,一条弦的长为
,一条弦的长为![]() ,那么这条弦的弦心距等于______
,那么这条弦的弦心距等于______![]()
8、已知⊙![]() 的直径为
的直径为![]() ,如果圆心
,如果圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,那么直线
,那么直线![]() 与⊙
与⊙![]() 有______个公共点
有______个公共点
9、如图,![]() 和
和![]() 是⊙
是⊙![]() 的直径,
的直径,![]() ,若
,若![]() ,则
,则![]() 的度数是_____
的度数是_____

10、正八边形的中心角等于______度
11、已知,数据![]() 的平均数为12,那么数据
的平均数为12,那么数据![]() 的平均数为______
的平均数为______
12、数据![]() 的方差为______
的方差为______
13、已知数据![]() 的中位数是3,那么
的中位数是3,那么![]() =_____(写出一个符合条件的数)
=_____(写出一个符合条件的数)
14、若两圆相切,半径分别为![]() 和
和![]() ,则两圆的圆心距的长为______
,则两圆的圆心距的长为______
15、已知⊙![]() 和⊙
和⊙![]() 相切,⊙
相切,⊙![]() 的半径长为
的半径长为![]() ,
,![]() ,那么⊙
,那么⊙![]() 的半径长等于_______
的半径长等于_______![]()
16、若正六边形的边长为2,则此正六边形的边心距为______
17、要使正五边形绕着它的中心旋转后能与它本身重合,至少要旋转______度
18、已知⊙![]() 的半径为5,两条平行弦的长分别为6和8,那么这两条弦之间的距离为______
的半径为5,两条平行弦的长分别为6和8,那么这两条弦之间的距离为______
三、解答题(本大题共7题,满分78分)
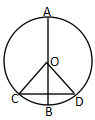
19、(本题满分10分)如图,已知![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是弦,且
是弦,且![]() ,如果半径是
,如果半径是![]() ,
,![]() ,求
,求![]() 的长
的长
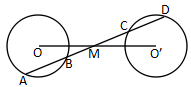
20、(本题满分10分)如图,等圆⊙![]() 与⊙
与⊙![]() 外离,
外离,![]() 为
为![]() 的中点,直线
的中点,直线![]() 过点
过点![]() ,交⊙
,交⊙![]() 与⊙
与⊙![]() 于点
于点![]() 。求证:
。求证:![]()
21、(本题满分10分)今年3月5日,某中学组织六、七年级200位学生参与了“走出校门,服务社会”的活。该校某数学学习小组的同学对那天参与打扫街道、敬老院服务和社区文艺演出的三组人数进行分别统计,部分数据如图所示。(1)参与社区文艺演出的学生人数是_____人,参与敬老院服务的学生是_____人;(2)该数学学习小组的同学还发现,六、七年级参与打扫街道的学生人数分别比参与敬老院服务的学生人数多了40%和60%。求参与敬老院服务的六、七年级学生分别有多少人?
22、(本题满分10分)某校为了了解八年级学生(共350人)的身体素质情况,体育老师对八(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示
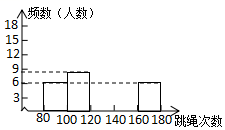
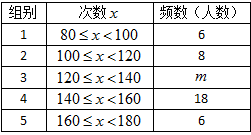
请结合图表完成下列问题:
(1)表中的![]() =____
=____
(2)请把频数分布直方图补充完整
(3)这个样本数据的中位数落在第_____组
(4)若八年级学生一分钟跳绳次数(![]() )合格要求是
)合格要求是![]() ,则估计八年级学生中一分钟跳绳成绩不合格的约几人?(要有解题过程)
,则估计八年级学生中一分钟跳绳成绩不合格的约几人?(要有解题过程)
23、(本题满分10分)如图,已知![]() 是⊙
是⊙![]() 中的弦,且
中的弦,且![]() ,
,![]() 分别是
分别是![]() 的中点,求证:
的中点,求证:![]()

24、(本体满分12分)如图,已知⊙![]() 的圆心在直线
的圆心在直线![]() 上运动
上运动
(1)若⊙![]() 半径为2,当⊙
半径为2,当⊙![]() 和
和![]() 轴相切时,求点
轴相切时,求点![]() 的坐标
的坐标
(2)若⊙![]() 半径为2,当⊙
半径为2,当⊙![]() 和
和![]() 轴相切时,求点
轴相切时,求点![]() 的坐标
的坐标
(3)若要让⊙![]() 与
与![]() 轴、
轴、![]() 轴都相切时,则⊙
轴都相切时,则⊙![]() 的半径是多少?
的半径是多少?
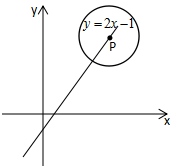
25、(本题满分14分)如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,
上一点,![]() ,点
,点![]() 是边
是边![]() 上一点,以点
上一点,以点![]() 为圆心,
为圆心,![]() 为半径作圆,经过点
为半径作圆,经过点![]() ,点
,点![]() 是边
是边![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 重合),作
重合),作![]() ,交射线
,交射线![]() 于点
于点![]()
(1)用直尺圆规做出圆心![]() ,并求圆
,并求圆![]() 的半径长(保留作图痕迹)
的半径长(保留作图痕迹)
(2)当点![]() 的边
的边![]() 上时,设
上时,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出它的定义域
的函数解析式,并写出它的定义域
(3)联结![]() ,当
,当![]() 与
与![]() 相似时,推理判断以点
相似时,推理判断以点![]() 为圆心,
为圆心,![]() 为半径的圆
为半径的圆![]() 与圆
与圆![]() 可能产生的各种位置关系
可能产生的各种位置关系


孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...