2018年合肥中考数学压轴试题【精选word版 含答案解析】

2018年合肥中考数学压轴试题【精选word版 含答案解析】

由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！

考生注意:本卷共八大题,计23小题,满分150分,考试时间120

一、选择题(本题共10小题,每题4分,共40分.每小题有四个答,其中有且只有个答案是正确的,请把正确答案的代号,写在题后的括号内,答对的得4分,答错、不答或答案超过一个的一律得0分)

1.2018的相反数是

A.-2018   B.2018    C D.

2.如图,a∥b,含30°角的三角板的直角顶点在直线b上,一个锐角的顶点在直线a上,

若∠1=20°,则∠2的度数是

A.20°   B.40°     C.50°   D.60°

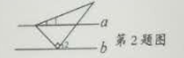
3.2017年11月8日-10日,美国总统特朗普对我国进行国事访向,访问期间,中美两国企业签约项目总金额达2500亿美元,这里“2500亿”用科学记数法表示为

A.2.5×103     B.2.5×1011      C.0.25×1012    D2500×108

4.如图是由四个大小相同的正方体组成的几何体,它的主视图是

5.估计-2的值应该在

A.-1-0之间     B.0-1之间      C.1-2之间     D.2-3之间

6.一元一次不等式组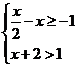 的解集在数轴上表示正确的是

17.如图是某班学生篮球运球成绩频数分布直方图,根据图中的信息,这组数据的中位数

与众数是

A.10人、20人   B. 13人、14人

C.14分、14分  D.135分、14分

8.如图,一次函数另=-x与二次函数为=ax2+bx+c的图象相交于点M,N,则关于x

的一元二次方程ax2+(b+1)x+c=0的根的情况是

A.有两个不相等的实数根    B.有两个相等的实数

C.没有实数根              D.以上结论都正确

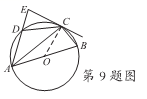
9.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线AD的延长线交于点E,若点D是弧AC的中点,且∠ABC=70°,则∠AEC等于

A.80°    B.75°      C.70°     D.65°

10.如图,矩形ABCD中,AB=4,BC=2,把矩形ABCD沿过点A的直线AE折叠点D落在矩形ABCD内部的点D处,则CD的最小值是

A.2   B. C.   D.

二、填空题(本题有4小题,每小题5分,共20分)

11.计算: =           

12.因式分解:a3-16ab2=          

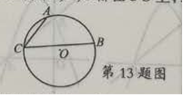
13.如图,点A,B,C都在⊙O上,∠ACB=60°,⊙O的直径是6,则劣弧AB的长是

14.在△ABC中,AB=6cm,点P在AB上,且∠ACP=∠B,若点P是AB的三等分点，则AC的长是

           .

三、(本题有2题,每题8分,共16分)

15.先化简,再求值: ，其中x=-4

16.清朝数学家梅文鼎的著作《方程论》中有这样一道题:山田三亩,场地六亩,共折实田四亩七分;又山田五亩,场地三亩,共折实田五亩五分,问每亩山田折实田多少,

每亩场地折实田多少?

译文为:假如有山田3亩,场地6亩,其产粮相当于实田4.7亩;又山田5亩,场地3亩,其产粮相当于实田5.5亩,问每亩山田和每亩场地产粮各相当于实田多少亩?请你解答

四、(本题有2题,每题8分,共16分)

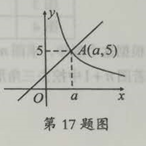
17.已知:如图,一次函数y1=x+2与反比例函数y2=(x>0)的图象交于点A(a,5)

(1)确定反比例函数的表达式;

(2)结合图象,直接写出x为何值时,y1<y2

18.在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)

(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到

△A2B2C2;

(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由

五、(本题有2题,每题10分,共20分)

19.观察下列图形,把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的

一个小三角形(如图1),对剩下的三个小三角形再分别重复以上做法,……,据此

解答下面的问题

填写下表:

(2)根据这个规律,求图n中挖去三角形的个数wn;(用含n的代数式表示)

(3)若图n+1中挖去三角形的个数为wn+1,求wn+1-Wn

20.如图,在一座小山上建有一座铁塔AD,小明站在C处测得小山顶A的仰角为30°,

铁塔顶端的D的仰角为45°,若铁塔AD的高度是100m,试求小山的铅直高度AB(精确到0.1m)(参考数据: =1.414. =1.732)

六、(本题共2分)

2.小明学习电学知识后,用四个开关按键(每个开关按键闭合的可能性相等)、一个电源和一个灯泡设计了一个电路图

(1)若小明设计的电路图(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;

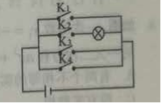
(2)若小明设计的电路图(四个开关按键都处于打开状态)如图所示,求同日时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)

七、(本题共12分)

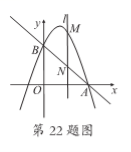
22已知:如图,抛物线y=-x2+bx+C经过点B(0,3)和点A(3,0)

()求该抛物线的函数表达式和直线AB的函数表达式;

(2)若直线l⊥x轴,在第一象限内与抛物线交于点M,与直线AB交于点N,请在备用图上画出符合题意的图形,并求点M与点N之间的距离的最大值或最小值,以及此时点M,N的坐标

八.（本题共14分）

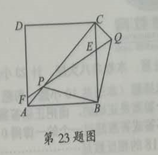
23.如图，正方形ABCD、等腰Rt△BPQ的顶点P在对角线AC上(点P与A、C不重合),Qp与BC交于E, QP延长线与AD交于点F,连接CQ

(1)①求证:AP=CQ

②求证:PA=AF·AD;

(2)若AP:PC=1:3,求tan∠CBQ

2018年合肥中考数学压轴试题参考答案及解析

选择题(本题共10小题,每题4分,共40分.每小题有四个答案,其中有且只有个答案是正确的,请把正确答案的代号,写在题后的括号内)

9.B提示:连接OC,∵CE是⊙O的切线,∴∠OCE=900,∵AB是⊙O的直径,

∠ACB=90°∴∠BAC=90°-70°=20°∴OA=OC∴∠OAC=∠OCA=20°

∵四边形ABCD内接于⊙O,∴∠EDC=∠ABC=70°,∵点D是弧AC的中点,

∴∠DAC=∠DCA=∠EDC=35°

∴∠ECD=90°-20°-35°=35°,

∴∠AEC=180°-70°-35°=75°

10.C 提示:根据题意,点D’在以点A为圆心,AD为半径且在矩形ABCD内部的圆

弧上,连接AC交圆弧于点D’,由勾股定理得AC= ,所以CD’

的最小值为

二、填空题(本题有4小题,每小题5分,共20分)

11.4

12.a(a+4b)(a-4b)

13.

14.

解析:由∠ACP=∠B,∠A=∠A,可得△ACP∽△ABC.

即AC2=AP·AB.

分两种情况:

AP= AB=2cm,AC2=2×6=12,

AC= = cm;

AP= AB=4cm,AC2=4×6=24,

AC= = (填对又一个得3分,两个5分)

三、(本题有2题,每题8分,共16分)

15.解

16.解:设每亩山田产粮相当于实田x亩,每亩场地产粮相当于实田y亩

可列方程组为 （5分）

解得 .答:每亩山田相当于实田0.9亩,每亩场地相当于实田亩.(8分)

四、(本题有2题,每题8分,共16分)

17.解

(1)∵点A(a,5)在一次函数y1=x+2的图象上

∴5=a+2,∴a=3,点A坐标为(3,5)

∵点A(3,5)在反比例函数的图象上,∴5= ∴

反比例函数的表达式为y2= (x>0);(5分)

(2)由图象可知,当0<x<3时,y1<y2.(8分)

18.解

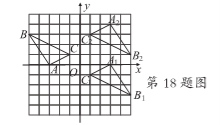
(1)如图所示,(5分)

(2)是,对称中心的坐标是(0,2).(8分)

五、(本题有2题,每题10分,共20分)

19.解

(1)图4挖去三角形的个数为33+32+3+1;(或40)(3分)

(2)wn=3n-1+3n-2+…+32+3+1;(6分)

(3)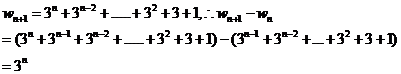 .(10分)

20.解:设AB=x(m),在Rt△ABC中

∵tan30°=

BC== (3分)

在Rt△BCD中,∵tan45°= (6分)

∵AD+AB=BD,∴100+x=x,

解得x≈136.6(m),(9分)

答:小山的铅直高度AB约为136.6m.(10分)

六、(本题共12分

21.解

(1)一共有四个开关按键,只有闭合开关按键K2,灯泡才会发光,所以P(灯泡发光)=

(4分)

(2)用树状图分析如下

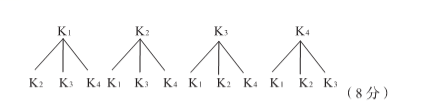
一共有12种不同的情况,其中有6种情况下灯泡能发光,所以P(灯泡发光)

(12分)

七、(本题共12分)

(1)∵抛物线y=-x2+bx+c经过点B(0,3)和点A(3,0),

解得 抛物线的函数表达式是y=-x2+2x+3;(2分)

设直线AB:y=kx+m,根据题意得

解得

,直线AB的函数表达式是y=-x+3;(4分)

（2）如图,设直线l的横坐标为a,则点M的坐标为(a,-a2+2a+3),

点N的坐标是(a,-a+3),又点M,N在第一象限, ∴|MN|=-a2+2a+3-(-a+3)=-a2+3a

(7分)

又|MN|=-a2+3a=-(a2-3a+)+=

当a= 时,|MN|有最大值,最大值为,

即点M与点N之间的距离有最大值,(10分)

此时点M坐标为(，)点N的坐标为 (12分)

八、(本题共14分)

23.解

(1)①∴正方形ABCD,∴AB=CB,∠ABC=90°,∴∠ABP+∠PBC=90°,

∵△BPQ是等腰直角三角形,∴BP=BQ,∠PBQ=90°,∴∠PBC+∠CBQ=90°

∴∠ABP=∠CBQ,∴△ABP≌△CBQ,∴AP=CQ;(4分)

②∵正方形ABCD,∴∠DAC=∠BAC=∠ACB=45°,

∵∠PQB=45°,∠CEP=∠QEB,∴∠CBQ=∠CPQ,由①得△ABP≌△CBQ,∠ABP=∠CBQ

∵∠CPQ=∠APF,∴∠APF=∠ABP,∴△APF∽△ABP,

(9分)

(本题也可以连接PD,证△APF∽△ADP)

(2)由①得△ABP≌△CBQ,∴∠BCQ=∠BAC=45°,∵∠ACB=45°

∠PCQ=45°+45°=90°∴tan∠CPQ=

由①得AP=CQ

又AP:PC=1:3,∴tan∠CPQ ,

由②得∠CBQ=∠CPQ,∴tan∠CBQ=tan∠CPQ= (14分)