2018年福州中考数学模拟练习试题【word版】
由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看!
选择题:
cos60°的值等于( )
下列各组中的四条线段a、b、c、d为成比例线段的是( )
A.a=10,b=5,c=4,d=7 B.a=1,b=3,c=6,d=2
C.a=8,b=-4,c=4,d=2 D.a=9,b=![]() ,c=3,d=
,c=3,d=![]()
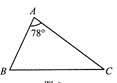 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的三角形与原三角形不相似的是( )
如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的三角形与原三角形不相似的是( )
在Rt△ABC中,∠C=90°,AB=4,AC=1,则sinB的值是( )
A.![]() B.
B.![]() C.
C.![]() D.4
D.4
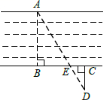 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( )
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,CE=10m,CD=20m,则河的宽度AB等于( )
A.60m B. 40m C. 30m D. 20m
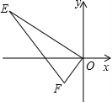 如图,E(-4,2),F(-1,-1),以O为位似中心,按比例尺1:2把△EFO缩小,点E的对应点的坐标( )
如图,E(-4,2),F(-1,-1),以O为位似中心,按比例尺1:2把△EFO缩小,点E的对应点的坐标( )
A.(-2,1) B.(2,-1)
C.(2,-1)或(-2,1) D.(8,-4)或(-8,4)
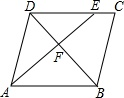 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.3:4 B.9:16 C.9:1 D.3:1
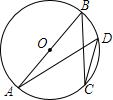 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,cosD=
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,cosD=![]() ,则AB的长为( )
,则AB的长为( )
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
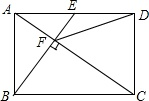 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:
①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .
.
其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
因为sin30°=![]() ,sin210°=
,sin210°=![]() ,所以sin210°=sin(180°+30°)=-sin30°;因为sin45°=
,所以sin210°=sin(180°+30°)=-sin30°;因为sin45°=![]() ,sin225°=
,sin225°=![]() ,所以sin225°=sin(180°+45°)=﹣sin45°,由此猜想,推理知:一般地当α为锐角时有sin(180°+α)=﹣sinα,由此可知:sin240°=()
,所以sin225°=sin(180°+45°)=﹣sin45°,由此猜想,推理知:一般地当α为锐角时有sin(180°+α)=﹣sinα,由此可知:sin240°=()
![]() B.
B.![]() C.
C.![]() D.
D.![]()
填空题:
 如果在比例1:2000000的地图上,A,B两地的图上距离为3.8厘米,那么A,B两地的实际距离为 千米.
如果在比例1:2000000的地图上,A,B两地的图上距离为3.8厘米,那么A,B两地的实际距离为 千米.
在△ABC中,如果∠A、∠B满足![]() 那么∠C= .
那么∠C= .
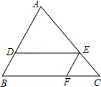
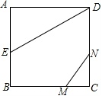 如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,若AB=9,BD=3,BF=5,则FC的长为 .
如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB,若AB=9,BD=3,BF=5,则FC的长为 .
如图,正方形ABCD的边长为4,AE=EB,MN=2,线段MN的两端在CB、CD上滑动,当CM= 时,△ADE与△CMN相似.
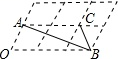
如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是 .
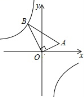 如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=
如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=![]() ,反比例函数
,反比例函数![]() 的图象经过点B,则k的值为 .
的图象经过点B,则k的值为 .
三、2018年福州中考数学模拟练习试题作图题:
17.如图,点A的坐标为(3,2),点B坐标为(3,0).作如下操作:
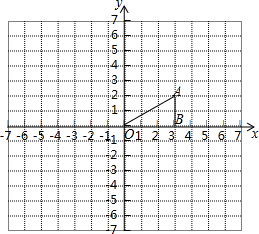 ①以点A为旋转中心,将△ABO顺时针方向旋转90°,得到△AB1O1;
①以点A为旋转中心,将△ABO顺时针方向旋转90°,得到△AB1O1;
②以点O为位似中心,将△ABO放大,得到△A2B2O,使相似比为1:2,且点A2在第三象限.
(1)在图中画出△AB1O1和△A2B2O;
(2)请直接写出点A2的坐标: .
四、解答题:
18.计算:![]() .
.
如图,在△ABC中,AB=6,BC=4,点D在BC的延长线上,且∠BAC=∠D,求BD的长
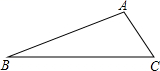
已知:如图,在△ABC中,AC=10,sinC=![]() ,sinB=
,sinB=![]() ,求AB.
,求AB.
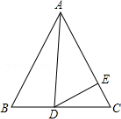 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.
阅读材料:一般地,当α,β为任意角时,tan(α+β)与tan(α-β)的值可以用下面的公式求得:![]()
例如: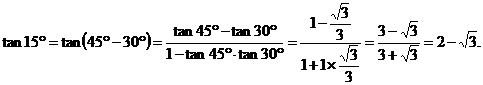
根据以上材料,解决下列问题:
(1)求tan75°的值;
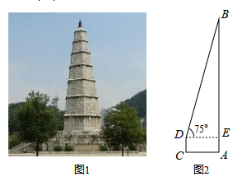
(2)都匀文峰塔,原名文笔塔,始建于明代万历年间,系五层木塔,文峰塔的木塔年久倾毁,仅存塔基,1983年,人民政府拨款维修文峰塔,成为今天的七层六面实心![]() 石塔(图1),小华想用所学知识来测量该铁搭的高度,如图2,已知小华站在离塔底中心A处6米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.72米,请帮助小华求出文峰塔AB的高度.(精确到1米,参考数据
石塔(图1),小华想用所学知识来测量该铁搭的高度,如图2,已知小华站在离塔底中心A处6米的C处,测得塔顶的仰角为75°,小华的眼睛离地面的距离DC为1.72米,请帮助小华求出文峰塔AB的高度.(精确到1米,参考数据![]() ).
).
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D.
 求证:AC2=AD·BD;
求证:AC2=AD·BD;
若![]() ,求线段BC的长.
,求线段BC的长.
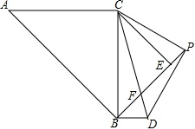
24.如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=![]() ,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F.
,点P为线段BE延长线上一点,连接CP以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F.
 (1)求证:
(1)求证:![]() ;
;
(2)连接BD,请你判断AC与BD有什么位置关系?并说明理由;
(3)设PE=x,△PBD的面积为S,求S与x之间的函数关系式.
25.在平面直角坐标系xOy中,抛物线y=-x2+mx+n与x轴交于点A,B(A在B的左侧).
(1)抛物线的对称轴为直线x=-3,AB=4.求抛物线的表达式;
(2)平移(1)中的抛物线使平移后的抛物线经过点O,且与x正半轴交于点C,记平移
后的抛物线顶点为P,若△OCP是等腰直角三角形,求点P的坐标;
 (3)当m =4时,抛物线上有两点M(x1,,y1)和N(x2,,y2),若x1< 2,x2>2,x1+ x2 > 4,
(3)当m =4时,抛物线上有两点M(x1,,y1)和N(x2,,y2),若x1< 2,x2>2,x1+ x2 > 4,
试判断y1与y2的大小,并说明理由.

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...