2018年钦州中考数学冲刺试题word版（含答案）

此试题可能存在乱码情况，在查看时请点击右上角全屏查看

2018年钦州中考数学冲刺试题

                  （考试时间：120分钟   满分120分）

一.填空：（每小题2分，共20分）

1．计算：(－1) ×（－2） =         ．

2．如图，已知AB∥CD，则∠A =        度．

3．分解因式 x3－xy2=            。

4．在函数中，自变量x的取值范围是      。

5．截至2009年6月5日止，全球感染H1N1流感病毒有21240人，感染人数用科学计数法表示为           人．

6．方程2 x2－18=0的解是           ．

7．若100个产品中有95个正品、5个次品，从中随机抽取一个，

恰好是次品的概率是       ．

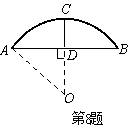
8．某蔬菜基地的圆弧形蔬菜大棚的剖面如图（2）所示，已知

AB＝16m，半径OA＝10m，则中间柱CD的高度为     m．

9．一个扇形所在圆的半径为3cm，扇形的圆心角为120°，则扇形的面积

是     cm2． （结果保留）

10．如图，是用火柴棍摆成的边长分别是1，2，3 根火柴棍时的正方形．当边长为n根火柴棍时，设摆出的正方形所用的火柴棍的根数为，则＝             ． （用n的代数式表示）

二、选择题（每小题3分，共24分）

11．－8的相反数是（   ）

A．  8    B．－8         C．            D．  

12．已知两圆的半径分别为2和3，圆心距为5，则这两圆的位置关系是（   ）．

A.外离       B. 相交       C.外切       D.内切

13．下列四边形：①正方形、②矩形、③菱形，对角线一定相等的是（   ）

A．①②③              B．①②                            C．①③                            D．②③

14．在一次射击测试中，甲、乙、丙、丁的平均环数均相同，而方差分别为8.7，9.1，6.5，7.7，则这四人中，射击成绩最稳定的是（   ）

A．甲                              B．乙                                 C．丙                                D．丁

15、tan30°的值等于（   ）

A.                                               B.                                                         C.                                                         D.

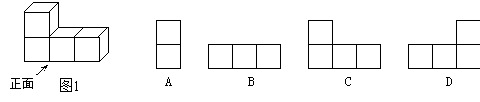
16图1中几何体的主视图是（   ）

17．若分式的值为零，则x的值是（   ）

A．1       B．0        C．－1        D．±1

18．如图，抛物线y＝ax2＋bx＋c的对称轴是x＝，小亮通过

观察得出了下面四条信息：

①c＜0，②abc＜0，③a－b＋c＞0，④2a－3b＝0．

你认为其中正确的有（   ）

A．1个       B．2个       C．3个       D．4

三、解答题：(共76分)

19、（本题7分）计算:

20、（本题7分）解方程：

21．（本题8分）如图，E是正方形ABCD的边DC上的一点，过A作AF⊥AE，交CB延长线于点F，求证：△ADE≌△ABF.

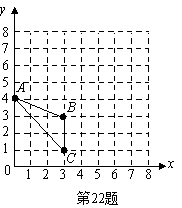
22．（本题10分）已知在平面直角坐标系中的位置如图10所示．

（1）分别写出图中点的坐标；

（2）画出绕点按顺时针方向旋转；

（3）求点旋转到点所经过的路线长（结果保留）．

23、（本题10分）右边下面两图是根据某校初三（1）班同学的上学方式情况调查所制作的条形和扇形统计图，请你根据图中提供的信息,解答以下问题：

(1) 求该班学生骑自行车的人数有

（2）求该班学生人数     人．

并将条形统计图补充完整；

（3）若该校初三年有600名学生，

试估计该年级乘车上学的人数.

24．（本题10分）某冰箱厂为响应国家“家电下乡”号召，计划生产、两种型号的冰箱100台．经预算，两种冰箱全部售出后，可获得利润不低于 47500元，不高于48000元，两种型号的冰箱生产成本和售价如下表：

   （1）冰箱厂有哪几种生产方案？

   （2）该冰箱厂按哪种方案生产，才能使投入成本最少？“家电下乡”后农民买家电（冰箱、彩电、洗衣机）可享受13%的政府补贴，那么在这种方案下政府需补贴给农民多少元？

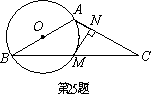
25、（本题12分）如图5，在中，，以为直径的交于点， 于点．

（1）求证是的切线；

（2）若，求以直径AB，弦BC和围成图形的面积（结果保留）．

、

26．（本题12分）如图，抛物线与轴交于两点，与轴交于点．

（1）求三点的坐标；

（2）证明为直角三角形；

（3）在抛物线上除点外，是否还存在另外一个点，使是直角三角形，若存在，请求出点的坐标，若不存在，请说明理由．

2018年钦州中考数学冲刺试题参考答案

一．１．2  2．120 3．x（x＋y）（x－y）4．ｘ≥ 5．2.124×104 6．3和－3   7．   8．4   9．3 10．２ｎ（ｎ＋１）二．11. A 12.C 13.B 14. C　15. D 16.D 17.A18.B

19．2+

20．X1=3，X2=1

21．证明：∵ABCD是正方形  ∴ ∵AF⊥AE  

∴．在和中

∵　　∴△ADE≌△ABF

22．解：（1）、（2）图略

（3），  =

23．解：（１）8　(2）该班学生人数为（人）  图画对（略）

（3）该年级乘车上学的人数约为

24．. 解：（1）设生产型冰箱台，则型冰箱为台，由题意得：

    解得： 是正整　∴x取38，39或40．

    有以下三种生产方案：

（2）设投入成本为元，由题意有：

∴y随的增大而减小∴当时，有最小值．

即生产型冰箱40台，型冰箱50台，该厂投入成本最少

此时，政府需补贴给农民

25．（1）证明：连接．

∵，∴，∵，∴．

∴，∴．

又，∴，点在上，∴是的切线

（2）S=

26．解：（1）抛物线与轴交于两点，

．即．解之得：．

∴点的坐标为 ，将代入，

得点的坐标为（0，2）

（2），，则，

是直角三角形．

（3）将代入，得．

点坐标为．

7