2018年梧州中考数学冲刺试题word版（含答案）

此试题可能存在乱码情况，在查看时请点击右上角全屏查看

2018年钦州中考数学冲刺试题

说明：1．本试卷共8页（试题卷4页，答题卷4页），满分120分，考试时间120分钟．

　　　2．答题前，请将学校、班别、姓名、考场、座位号写在答题卷指定的位置，答案写在答题卷相应的区域内，在试题卷上答题无效．

一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是正确的，每小题选对得3分，选错、不选或多选均得零分．）

1. 4的平方根是 (　 　)

A.±2        B. 2              C. ±4　   D. 4

2. 计算的结果是（    ）

A.       　B.   　C.       D.

3. 若∠α＝30°，则∠α的补角是（    ）

   A.30°         B.60°     C.120°      D.150°

4. 甲、乙、丙、丁四位同学五次汉语听写成绩统计如下表．如果从这四位同学中，选出一位成绩较好且状态稳定的同学参加全国汉语听写大赛，那么应选（　　）

A. 甲                      B. 乙                    C. 丙                     D. 丁

5. 函数中自变量x的取值范围是(　　)

A. x＞2              B. x≤2                            C. x≥2                            D. x＜2

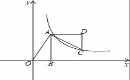
6. 如图，平面直角坐标系中，OB在x轴上，∠ABO=90°，点A

的坐标为（1，2），将△AOB绕点A逆时针旋转90°，点O

的对应点C恰好落在双曲线（x＞0）上，则k的值为（　　）

A. 2         B. 3       C. 4        D. 6

7. 一个正多边形，它的每一个外角都等于45°，则该正多边形是(　 　)

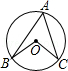A. 正六边形              B. 正七边形                            C.正八边形                            D. 正九边形        

8. 如图，已知圆心角∠BOC＝100°，则圆周角∠BAC的大小是（　　）

  A. 50°                   B. 55°      C. 60°                  D. 65°

9. 如图所示，∠AOB的两边OA、OB均为平面反光镜，∠AOB＝35°，

在OB上有一点E，从E点射出一束光线经OA上的点D反射后，

反射光线DC恰好与OB平行，则∠DEB的度数是(　　)

A. 35°         B. 120°         C. 110°       D. 70°

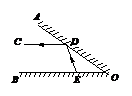
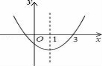
10. 如图，二次函数y＝ax2+bx+c的图象开口向上，对称轴为直线

x＝1，图象经过（3，0），下列结论中，正确的一项是（　　）

A.  abc＜0                B. a－b＋c＜0   C. 4ac－b2＜0  D. a＋b＜0

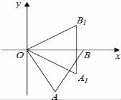
11. 如图所示，边长为2的正三角形ABO的边OB在x轴上，将△ABO

绕原点O逆时针旋转30°得到三角形OA1B1，则点A1的坐标为(　　)

A.（，1）   B.（2，－1）  C.（1，－）   D.（，－1）

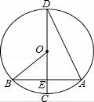
12. 如图，已知⊙O的半径OB为3，且CD⊥AB，∠D＝15°．

则OE的长为（　　）

A.        B.                  C.         D. 3

二、填空题（本大题共6小题，每小题3分，共18分．请将答案写在答题卷上）

13. 计算：－2－（－3）＝　　　　　　．

14. 分解因式：4a2－16＝　　　　　　．

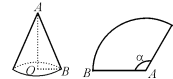
15. 如图，圆锥的底面半径OB为10cm，它的展开图扇形的半

　　径AB为30cm，则这个扇形圆心角的度数是_    _．

16. 已知点P（a，b）在直线上，点Q（－a，2b）

在直线y＝x＋1上，则代数式a2－4b2－1＝　　 ．

17.把直线y＝－x＋3向上平移m个单位后，与直线y＝2x＋4的交点在第一象限，则m的取

值范围是　　　　　　．

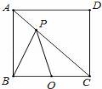18. 如图，正方形ABCD的边长为8，O是BC的中点，点P是

对角线AC上一动点，则PO＋PB的最小值为　　　　　　．

三、解答题（本大题共8小题，满分66分，请将答案写在答题卷上）

19. (6分)计算： 2sin60°－＋

20.（6分）先化简，再求值：（x＋2）（x－2）－（x＋1）2，其中x =－3．

21. (6分) 如图，在△ABC中，AB＝CB，∠ABC＝90º，D为AB延

长线上一点，点E在BC边上，且BE＝BD，连结AE、DE、DC.

     求证：△ABE≌△CBD；

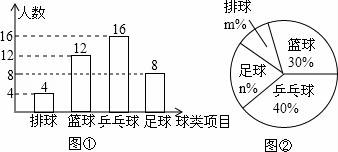
22.（8分）某中学九（1）班为了了解全班学生喜欢球类活动的情况，采取全面调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：

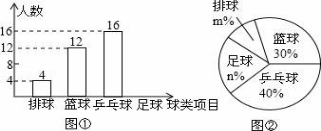
（1）九（1）班的学生人数为　　　，

　　并把条形统计图补充完整；

（2）扇形统计图中m＝　　　，n＝　　　　，表示“足球”的扇形的圆心角是　　　　度；（3）排球兴趣小组4名学生中有3男1女，现在打算从中随机选出2名学生参加学校的排

球队，请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率．

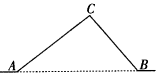
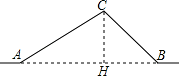
23.（8分）市新修建的南环公路从A地到B地需经过C地.如图中 AC＝10千米，∠CAB＝25°，∠CBA＝37°，因城市规划的需要，将在A、B两地之间修建一条笔直的公路．

    (1)求改直后的公路AB的长；

(2)问公路改直后比原来缩短了多少千米?

(sin25°=0.42，cos25°=0.91，sin37°=0.60，tan37°=0.75)

24.（10分）某镇枇杷园的枇杷除了运往市区销售外，还可以让市民亲自去园内采摘购买．已知今年3月份该枇杷在市区、园区的销售价格分别为6元／千克、4元／千克，今年3月份一共销售了3000千克，总销售额为16000元．

  (1)3月份该枇杷在市区、园区各销售了多少千克?

  (2)4月份是枇杷旺季且适逢“三月三”小长假,

为了促销，枇杷园决定4月份将该枇杷在市区、

园区的销售价格均在3月份的基础上降低a％，预

计这种枇杷在市区、园区的销售量将在3月份的

基础上分别增长30％、20％，要使4月份该枇杷

的总销售额不低于18360元，则a的最大值是多少?

25.（10分）如图，AB是⊙O的直径，点E是上的一点，∠DAC＝∠AED.

(1)求证：AC是⊙O的切线；

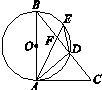(2)若点E是的中点，连接AE交BD于点F，当BD＝5，CD＝4

时，求DF的值．

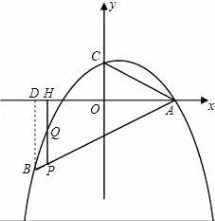
26.（12分）如图，二次函数的图象经过点A（4，0），B（－4，－4），且与y轴交于点C．

（1）试求此二次函数的解析式；

（2）试证明：∠BAO＝∠CAO（其中O是原点）；

（3）若P是线段AB上的一个动点（不与A、B重合），过P作y轴的平行线，分别交此二次函数图象及x轴于Q、H两点，试问：是否存在这样的点P，使PH＝2QH？若存在，请求出点P的坐标；若不存在，请说明理由。

2018年梧州中考数学冲刺试题参考答案

一、选择题：

二、填空题

13．1　 14．4（a＋2）(a－2)   15．120°　16. 1   17．m＞1   18.

三、解答题

19．解：原式＝2×－9＋1. 　…………………………………………………………（3分）

＝－8……………………………………………………………………（6分）

20．解：原式＝x2－4－x2－2x－1  ………………………………………………………（2分）

＝－2x－5　　 ………………………………………………………………（4分）

当x＝－3时，原式=－2×（－3）＝6－5＝1． …………………………………（6分）

21．（1）证明：如图1.

              ∵ ∠ABC＝90º，D为AB延长线上一点，

          ∴ ∠ABE＝∠CBD=90º . ……………（2分）

          在△ABE和△CBD中,

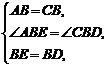
          ∴ △ABE≌△CBD. …………………… （6分）                                    

22．解：（1）40；……………………………………………………………………………（1分）

补全统计图如图所示； …………………………………………………………………（2分）

（2）10；20；72； …………………………………………………………………………（5分）

（3）根据题意画出树状图如下：

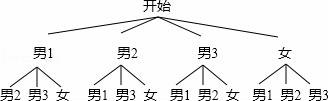……………………………………（7分）

一共有12种情况，恰好是1男1女的情况有6种，

∴P（恰好是1男1女）＝＝．………………………………………………………（8分）

23．解：（1）作CH⊥AB于H． ……………………………………………………………（1分）

在Rt△ACH中，CH＝AC•sin∠CAB＝AC•sin25°≈10×0.42＝4.2千米，

AH＝AC•cos∠CAB＝AC•cos25°≈10×0.91＝9.1千米，……………（3分）

在Rt△BCH中，BH＝CH÷tan∠CBA＝4.2÷tan37°≈4.2÷0.75＝5.6千米，…………（4分）

∴AB＝AH＋BH＝9.1＋5.6＝14.7千米．

故改直的公路AB的长14.7千米；  …………………………………………………（5分）

（2）在Rt△BCH中，BC＝CH÷sin∠CBA＝4.2÷sin37°≈4.2÷0.6＝7千米， …………（6分）

则AC＋BC－AB＝10＋7－14.7＝2.3千米．…………………………………………（8分）

答：公路改直后比原来缩短了2.3千米．

24．解：（1）设在市区销售了x千克，则在园区销售了（3000－x）千克，……………（1分）

则6x＋4（3000－x）＝16000，……………………………………………………（3分）

解得x＝2000 ， ……………………………………………………………………（4分）

3000－x＝000．

故今年3月份该枇杷在市区销售了2000千克，在园区销售了1000千克。………（5分）

（2）根据题意，得：

6（1－a%）×2000（1＋30%）＋4（1－a%）×1000（1＋20%）≥18360，

即：20400（1－a%）≥18360， ………………………………………………………（8分）

解得：a≤10．  ………………………………………………………………………（9分）

故a的最大值是10．   ………………………………………………………………（10分）

25.解：(1)证明：∵AB是⊙O的直径，

∴∠ADB＝∠ADC＝90°………………………………………………………………（1分）.

∵∠B＝∠AED＝∠CAD，∠C＝∠C，

∴∠C＋∠CAD＝∠C＋∠B＝90°，

∴∠BAC＝∠ADC＝90°. ……………………………………………………………（2分）

又∵AB是⊙O的直径，

∴AC是⊙O的切线． …………………………………………………………………（4分）

(2)可证△ADC∽△BAC，………………………………………………………………（6分）

∴＝，即AC2＝BC·CD＝36.

解得AC＝6. ………………………………………………………………………………（8分）

∵E是的中点，

∴∠DAE＝∠BAE.

∵∠CAF＝∠CAD＋∠DAE＝∠ABF＋∠BAE＝∠AFD，

∴CA＝CF＝6，  ………………………………………………………………………（9分）

∴DF＝CF－CD＝2.  …………………………………………………………………（10分）

26．解：（1）∵点A（4，0）与B（－4，－4）在二次函数图象上，

∴………………………………………………………………………（1分）

解得 …………………………………………………………………………………（3分）

∴二次函数解析式为y=－x2＋x＋2．………………………………………………（4分）

（2）过B作BD⊥x轴于点D，由（1）得C（0，2），………………………………（5分）

则在Rt△AOC中，tan∠CAO＝＝＝，…………………………………………（6分）

又在Rt△ABD中，tan∠BAD＝＝＝；…………………………………………（7分）

∵tan∠CAO＝tan∠BAD，

∴∠CAO＝∠BAO．…………………………………………………………………………（8分）

（3）由点A（4，0）与B（－4，－4），可得直线AB的解析式为y＝x－2，………（9分）

设P（x，x－2），（－4＜x＜4）；

则Q（x，－x2＋x＋2），……………………………………………………………（10分）

∴PH＝|x－2|＝2－x，QH＝|－x2＋x＋2|．

∴2－x＝2|－x2＋x＋2|．

当2－x＝－x2＋x＋4，

解得x1＝－1，x2＝4（舍去），

∴P（－1，－）………………………（11分）

当2－x＝x2－x－4，

解得x1＝－3，x2＝4（舍去），

∴P（－3，－）．

综上所述，存在满足条件的点，它们是P1（－1，－）与P2（－3，－）………（12分）