2018邯郸市中考数学模拟试题【精编版无答案】

由于格式问题此试题可能会出现乱码的情况

为了方便您阅读请点击右上角的全屏查看

2018邯郸市中考数学模拟试题

一、选择题（本大题共16个小题，1～10题，每小题3分；11～16小题，每小题2分，

   共42分，在每小题给出的四个选项中，只有一项符合题目要求的）

1．在实数，-，-、中，是无理数的是（   ）

   A．                                     B．-                                    C．-                                    D．

2．据统计，2017年石家庄市参加中考报名的学生共有8.7694万人。将8.7694用四舍五入

   法精确到百分位是（   ）

   A．8.769                                     B．8.770                                    C．8.76                                    D．8.77

3．若分式的值为0，则x的值为（   ）

   A．1                                     B．-1                                    C．±1                                    D．0

4．的平方根等于（   ）

   A．±3                                      B．-3                                     C．±9                                    D．9

5．（邯郸中考数学）下列命题中，与“同旁内角互补，两直线平行”成为互逆定理的是（   ）

   A．同旁内角不互补，两直线平行                                             B．同旁内角不互补，两直线不平行

   C．两直线平行，同旁内角互补                                               D．两直线不平行，同旁内角不互补

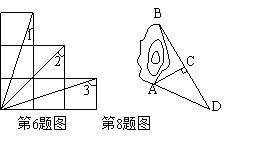6．如图为6个边长相等的正方形的组合图形，则∠1、∠2、∠3的和为（   ）

   A．90°                                     B．120°

   C．135°                                    D．150°

7．分式方程-2=的解为（   ）

   A．x=2                                      B．x=1

   C．x=-1                                    D．x=0

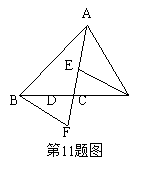
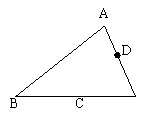
8．如图所示，为了测量出A，B两点之间的距离，在地面上找到一点C，连接BC，AC，

   使∠ACB=90°，然后在BC的延长线上确定D，使CD=BC，那么只要测量出AD的长

   度也就得到了A，B两点之间的距离，这样测量的依据是（   ）

              A．AAS                       B．SAS                                                        C．ASA                                    D．SSS

9．              对于实数x，我们规定[x]表示不大于x的最大整数，如[4]=4，[]=1，[-2.5]=-3．现

              对82进行如下操作：82        []=9        []=3        []=1，这样

              对82只需进行3次操作后变为1，类似地，对121只需进行多少次操作后变为1（   ）

              A．1                                     B．2                                    C．3                                    D．4

10．若a+b=3，则代数式（-a）÷的值为（   ）

              A．3                                     B．-3                                    C．                                    D．-

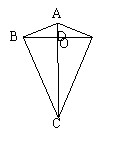
11．如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且BF∥CE，若

              AD=5，DF=2，则AE的长为（   ）

              A．2                                     B．3

              C．4                                                 D．5

12．对于“”，下面说法不正确的是（   ）

              A．它是一个无理数

              B．它是数轴上离原点个单位长度的点表示的数

              C．若a＜＜a+1，则整数a为2

              D．它表示面积为7的正方形的边长

13．一个底面为正方形的长方体体积为196cm3，高为4cm，则该长方体的表面积为（   ）

              A．200cm2                       B．210cm2                      C．220cm2                      D．294cm2

14．（邯郸中考数学）关于x的分式方程+5=有增根，则m的值为（   ）

              A．1                                     B．3                           C．4                           D．5

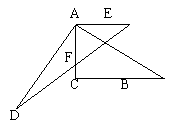
15．定义：两组邻边分别相等的四边形称为筝形．如图，在四边形ABCD中，AB=AD，

              BC=DC，AC与BD相交于点O，下列判断：①AC⊥BD ②AC、BD互相平分 ③AC

              平分∠BCD ④∠ABC=∠ADC=90°

              ⑤筝形ABCD的面积为AC•BD．

              正确的有（   ）

              A．①③④                       B．①③⑤

              C．①④⑤                      D．③④⑤

16．为助力衡水市争创“魅力中国城”活动，市环卫公司爱心小分队清理卫生死角内的垃圾，

              调用甲车3小时只清理了一半垃圾，为了加快进度，再调用乙车，两车合作1.2小时

              清理完另一半垃圾．设乙车单独清理全部垃圾的时间为x小时，依题意可列方程为（   ）

              A．+=1                                                                                                  B．+=1             

              C．+=                                                                                                  D．+=

卷II（非选择题，共78分）

二、（邯郸中考数学）填空题（本大题共3个小题；共10分。17～18小题各3分，19小题有两个空，每空

              2分，把答案写在题中横线上）

17．计算：+=          ．

18．若x+2的平方根是±2，2x+y+7的立方根是3，

              则6x3+y的算术平方根为          ．

19．如图，AC=AE，AD=AB，∠ACB=∠DAB=90°，

              ∠BAE=35°，AE∥CB，AC、DE交于点F．

（1）∠DAC=       ；

（2）猜想线段AF与BC的数量关系是          ．

三、解答题（本大题共7个小题；共68分。解答应写出文字说明、证明过程或演算步骤）

20．（本小题满分8分）

              对于实数a，b（a≠±b），我们定义两种运算：a⊕b=，a⊙b=．

（1）化简：m⊕n+2（m⊙n）；

（2）当x⊕1+x⊙1=0时，求x的值．

21．（本小题满分9分）

              嘉嘉用两张同样大小的长方形硬纸片拼接成一个面积为900cm2的正方形，如图所示，

              按要求完成下列各小题．

   （1）求长方形硬纸片的长和宽；

   （2）嘉嘉想用该正方形硬纸片制作一个体积512cm3的正方体的无盖笔筒，请你判断

        该硬纸片是否够用？若够用，求剩余的硬纸片的面积；若不够用，求缺少的硬纸

        片的面积．

22．（本小题满分9分）

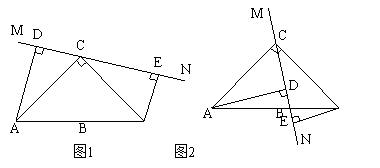
              如图，在△ABC中，D是AC上一点（CD＞AD），按要求完成下列各小题.（保留作

              图痕迹，不写作法，标明各顶点字母）

   （1）连接BD，求作△DEF（点E在线段CD上，点F在线段AC的右侧），使得△DEF

        ≌△DAB；

   （2）在（1）的条件下，作∠EFH=∠ABC，交CA的延长线于点H，并证明HF∥BC．

23．（邯郸中考数学）（本小题满分9分）

              如图1，这是由8个同样大小的立方体组成的魔方，体积为64．

   （1）求出这个魔方的棱长．

   （2）图中阴影部分是一个正方形ABCD，求出阴影部分的面积及其边长．

   （3）把正方形ABCD放到数轴上，如图2，使点A与-1重合，那么点D表示的数为

                   ．

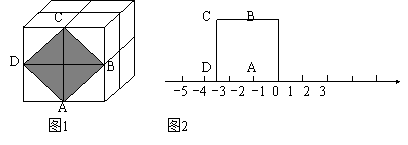24（邯郸中考数学）．（本小题满分10分）

              在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN

              于E．

   （1）当直线MN绕点C旋转到图1的位置时，求证：

        ①△ADC≌△CEB；②DE=AD+BE；

   （2）当直线MN绕点C旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给

        出证明；若不成立，说明理由．

25．（邯郸中考数学）（本小题满分11分）

              某市为创建全国文明城市，开展“美化绿化城市”活动，计划经过若干年使城区绿化总

              面积新增360万平方米．自2013年初开始实施后，实际每年绿化面积是原计划的1.6

              倍，这样可提前4年完成任务．

   （1）问实际每年绿化面积多少万平方米？

   （2）为加大创城力度，市政府决定从2016年起加快绿化速度，要求不超过2年完成，

        那么实际平均每年绿化面积至少还要增加多少万平方米？

26．（邯郸中考数学）（本小题满分12分）

              八年级一班数学兴趣小组在一次活动中进行了探究试验活动，请你和他们一起活动吧．

   【发现】如图1，AD是△ABC的中线，延长AD至点E，使ED=AD，连接BE，写出

                     图中全等的两个三角形_____________．

   【探究】如图2，EP是△DEF的中线，若EF=5，DE=3，设EP=x，求x的取值范围．

   【拓展】如图3，AD是△ABC的中线，∠BAC=∠ACB，点Q在BC的延长线上，QC

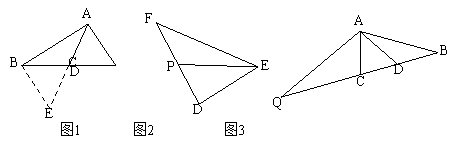                     =AB，若AD=2，试求AQ的长．