此试题可能存在乱码情况,在查看时请点击右上角全屏查看
2018年张家界中考数学模拟试题
题 号 | 一 | 二 | 三 | 总 分 |
得 分 |
|
|
|
|
考生注意:本试卷共三道大题,满分100分,时量120分钟。
一、选择题(3′ ×8=24′ )
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 |
|
|
|
|
|
|
|
|
1.![]() 2016的绝对值是
2016的绝对值是
A.![]() 2016 B.2016 C.
2016 B.2016 C.![]() D.
D.![]()
2.世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微笑的无花果,质量只有0.000000076克,将0.000000076用科学记数法表示为
A.7.6×108 B.0.76×10![]() C.7.6×10
C.7.6×10![]() D.0.76×109
D.0.76×109
3.不等式组![]() 的解集在数轴上表示正确的是
的解集在数轴上表示正确的是
A.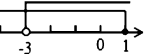 B.
B.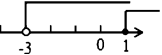
C.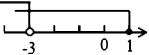 D.
D.![]()
 4.如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于
4.如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于
A.50° B.80°
C.65° D.115°
5.下列计算正确的是
A.![]() B.
B.![]()
 C.
C.![]() D.
D.![]()
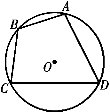
6.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为6,∠ABC=120°,则劣弧AC的长为
A.2π B.4π
C.5π D.6π
7.如图图形中,阴影部分面积相等的是

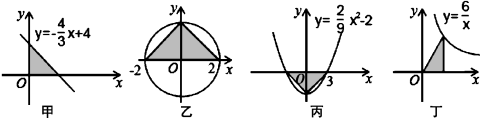
A.甲乙 B.甲丙 C.乙丙 D.丙丁
8.如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;
……,按此规律所作的第2016个菱形的边长为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(3′ ×6=18′ )
9.在函数![]() ,自变量x的取值范围是 .
,自变量x的取值范围是 .
10.分解因式:![]() .
.
11.已知:关于x的方程![]() 有一根为0,则m的值为 .
有一根为0,则m的值为 .
12.如图,在△ABC中,若DE∥BC,![]() ,DE=4cm,则BC的长为 cm.
,DE=4cm,则BC的长为 cm.
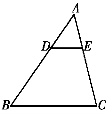
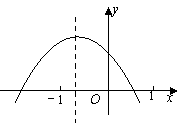
第12题图 第13题图
13.已知二次函数![]() 的图象如图所示,则下列关系式中错误的是 (填序号).
的图象如图所示,则下列关系式中错误的是 (填序号).
①a<0 ②c>0 ③![]() >0 ④
>0 ④![]() >0
>0
14.已知圆锥的母线长为2cm, 底面半径为1cm, 则该圆锥的侧面积为 cm2.
三、解答下列各题(58分)
15.计算:(5分) ![]() .
.
16.近视眼镜的度数y(度)与镜片焦距x(m)成反比例(即![]() (k≠0)),已知200度近视眼镜的镜片焦距为0.5m,求反比例函数解析式,并求出400度近视眼镜的镜片焦距.(5分)
(k≠0)),已知200度近视眼镜的镜片焦距为0.5m,求反比例函数解析式,并求出400度近视眼镜的镜片焦距.(5分)
17.(5分)如图,平行四边形ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,不说明理由.

18.(5分)先化简,再求值:先化简![]() ,然后在
,然后在![]() ,
,![]() ,0,1,2中选一个你认为合适的x的值,代入求值.
,0,1,2中选一个你认为合适的x的值,代入求值.
19.(5分)解不等式组![]() 并将解集在数轴上表示出来.
并将解集在数轴上表示出来.
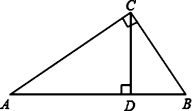
20.(5分)如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高.若AC=4,BC=3,求AB和AD的长.
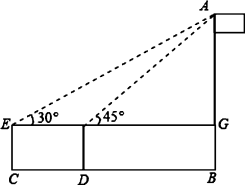
21.(5分)如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶
端A的仰角为45°,求旗杆AB的高度(![]() ,
,![]() )
)
22.(5分)某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过14吨(含14吨)时,每吨按政府补贴优惠价收费;每月超过14吨时,超过部分每吨按市场调节价收费.小英家1月份用水20吨,交水费29元;2月份用水18吨,交水费24元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少?
(2)小英家3月份用水24吨,她家应交水费多少元?
23.(8分)“端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
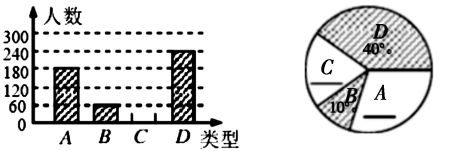
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率.
24.(10分)如图,已知抛物线![]() 与x轴交于
与x轴交于![]() ,
,![]() 两点(点A在点B的左边),与y轴交于点
两点(点A在点B的左边),与y轴交于点![]() ,连接BC.
,连接BC.
(1)求该抛物线的函数表达式;
(2)求抛物线的对称轴和直线BC的表达式;
(3)若点P为线段BC上一点(不与B,C重合),过P作PM平行于y轴,交抛物线于点M,交x轴于点N.求当M点的坐标为多少时,△BCM的面积最大,并求出此时的面积;
 (4)在(2)的结论下,抛物线的对称轴上是否存在一点E,使得NE垂直于CE?若存在,求点E的坐标;若不存在,说明理由.
(4)在(2)的结论下,抛物线的对称轴上是否存在一点E,使得NE垂直于CE?若存在,求点E的坐标;若不存在,说明理由.
2018年张家界中考数学模拟试题参考答案
一、选择题(3′ ×8=24′ )
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | C | A | D | A | B | B | D |
二、填空题(3′ ×6=18′ )
9、x≤2且x≠0 10、![]() 11、 1 12、12
11、 1 12、12
13、 ④ 14、2π
三、解答下列各题(58分)
15、![]()
16、![]() ,0.25
,0.25
17、(1)略(4分) (2)矩形(2分)
18、原式=![]() ,当x=2时,
,当x=2时,![]() .
.
19、![]() 数轴表示略
数轴表示略
20、![]() ,
,![]() .
.
21、旗杆AB的高度为5.65米
22、(1)设每吨水的政府补贴优惠价为x元,市场调节价为y元
![]() ,解得:
,解得:![]() .(3分)
.(3分)
(2)交水费:14×1+(24-14)×2.5=39(元) (5分)
23、(1)60÷10%=600(人)(2分) (2)120,20%,30%(4分)
(3)3200(人)(6分) (4)图略:P(C粽)=![]() .(8分)
.(8分)
24、(1)![]() (2分)
(2分)
(2)直线![]() ,
,![]() (4分)
(4分)
(3)![]()
![]() , △BCM的面积最大为
, △BCM的面积最大为![]() .(7分)
.(7分)
(4)![]()
 .(10分)
.(10分)

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...