2017年广东省中山一中协作体中考数学压轴题【精编解析版】
由于版式的问题,试题可能会出现乱码的现象,为了方便您的阅读请点击全屏查看
一、选择题(本大题10小题,每小题3分,满分30分)
1.实数﹣![]() 的相反数是()
的相反数是()
A.![]() B.3 C.﹣3 D.﹣
B.3 C.﹣3 D.﹣![]()
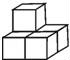
2.如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.地球平均半径约等于6 400 000米,6 400 000用科学记数法表示为()
A.64×105 B.6.4×105 C.6.4×106 D.6.4×107
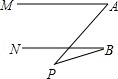
4.如图,直线MA∥NB,∠A=50°,∠B=20°,则∠P=()度.
A.20 B.25 C.30 D.35
5.下列计算正确的是()
A.a2+a2=a4 B.(a2)3=a5 C.2a2﹣a2=2 D.a5•a2=a7
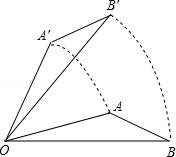
6.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是()
A.25° B.30° C.35° D.40°
7.下列命题是假命题的是()
A.若a>b,则ac2>bc2 B.若a>b,则a+c>b+c
C.若ac2>bc2,则a>b D.若a>b,b>c,则a>c
8.一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
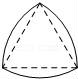
9.如图,“凸轮”的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成.已知正三角形的边长为1,则凸轮的周长等于()
A.![]() B.
B.![]() C.π D.2π
C.π D.2π
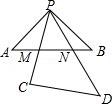
10.如图,将足够大的等腰直角三角板PCD的锐角顶点P放在另一个等腰直角三角板PAB的直角顶点处,三角板PCD绕点P在平面内转动,且∠CPD的两边始终与斜边AB相交,PC交AB于点M,PD交AB于点N,设AB=2,AN=x,BM=y,则能反映y与x的函数关系的图象大致是()
A.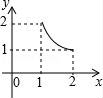 B.
B.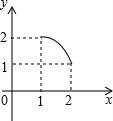 C.
C.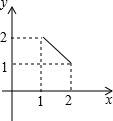 D.
D.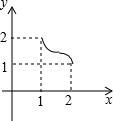
二、填空题(本大题6小题,每小题4分,共24分)
11.一个多边形的每一个外角都等于30°,则该多边形的内角和等于 .
12.已知![]() +|a﹣b+2|=0,则ab= .
+|a﹣b+2|=0,则ab= .
13.分解因式:﹣2a3+8a2﹣8a= .
14.关于x的一元二次方程kx2﹣2x+1=0有两个不相等的实数根,则k的取值范围是 .
15.如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为 .

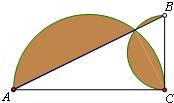
16.如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC、BC为直径画半圆,则图中阴影部分的面积为 (结果保留π).

三、解答题(一)(本大题3小题,每小题6分,共18分)
17.计算:|1﹣![]() |﹣2sin45°+(
|﹣2sin45°+(![]() )﹣2+
)﹣2+![]() .
.
18.先化简,再求值:(![]() ﹣
﹣![]() )÷
)÷![]() ,其中a=2,b=
,其中a=2,b=![]() .
.
19. 如图,在△ABC中,AB=BC,点D在AB的延长线上.
(1)用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作∠CBD的平分线BM;
②作边BC上的中线AE,并延长AE交BM于点F.
(2)求证:BF∥AC.

四、解答题(二)(本大题3小题,每小题7分,共21分)
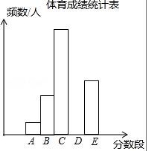
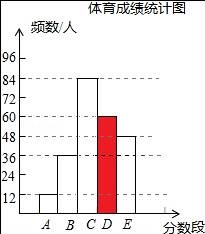
20. 为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.
分数段 | A | B | C | D | E | 合计 |
频数/人 | 12 | 36 | 84 | b | 48 | c |
频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
根据上面的信息,回答下列问题:
(1)统计表中,a= ,b= ,c= ;将频数分布直方图补充完整.
(2)小明说:“这组数据的众数一定在C中.”你认为小明的说法正确吗? (选填“正确”或“错误”).
(3)若成绩在27分及以上定为优秀,则该市30000名九年级学生中体育成绩为优秀的学生人数约有多少?
21.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.
(1)求证:AG=FG;
(2)求cos∠BGE的值.

22.某商店第一次用600元购进某品牌的笔记本若干本,第二次又用600元购进同样品牌的笔记本,但这次每本的进价是第一次的1.25倍,购进数量比第一次少了30本.
(1)求第一次每本笔记本的进价是多少元?
(2)商店以同一价格全部销售完毕后获利不低于420元,问每本笔记本的售价至少多少元?
五、解答题(三)(本大题3小题,每小题9分,共27分)
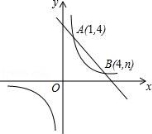
23.如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)直接写出关于x的不等式kx+b≤![]() 的解集.
的解集.
(3)点P是x轴上的一点,且使PA+PB最小,求△ABP的面积.
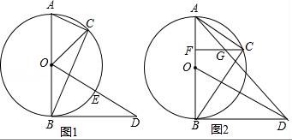
24.如图1,⊙O是△ABC的外接圆,AB是直径,OD∥AC,OD交⊙O于点E,且∠CBD=∠COD.
(1)求证:BD是⊙O的切线;
(2)若点E为线段OD的中点,判断以O、A、C、E为顶点的四边形的形状并证明;
(3)如图2,作CF⊥AB于点F,连接AD交CF于点G,求![]() 的值.
的值.
25.如图,四边形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°,点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(0<x<6).
(1)点G在四边形ABCD的边上时,x= ;点F与点C重合时,x= ;
(2)求出使△DFC成为等腰三角形的x的值;
(3)求△EFG与四边形ABCD重叠部分的面积y与x之间的函数关系式,并直接写出y的最大值.
2017年广东省中山一中协作体中考数学压轴题参考答案与试题解析
一、选择题(本大题10小题,每小题3分,满分30分)
1.实数﹣![]() 的相反数是()
的相反数是()
A.![]() B.3 C.﹣3 D.﹣
B.3 C.﹣3 D.﹣![]()
【考点】28:实数的性质.
【分析】根据相反数的定义选择正确的选项即可.
【解答】解:实数﹣![]() 的相反数是﹣(﹣
的相反数是﹣(﹣![]() )=
)=![]() ,
,
故选A.
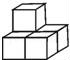
2.如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【考点】U2:简单组合体的三视图.
【分析】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
【解答】解:从左面看易得第一层有2个正方形,第二层最左边有一个正方形.
故选B.
3.地球平均半径约等于6 400 000米,6 400 000用科学记数法表示为()
A.64×105 B.6.4×105 C.6.4×106 D.6.4×107
【考点】1I:科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:6 400 000=6.4×106,
故选:C.
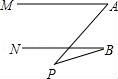
4.如图,直线MA∥NB,∠A=50°,∠B=20°,则∠P=()度.
A.20 B.25 C.30 D.35
【考点】JA:平行线的性质.
【分析】根据平行线的性质和三角形外角的性质即可得到结论
【解答】解:∵直线MA∥NB,∠A=50°,
∴∠1=∠A=50°,
∵∠B=20°,
∴∠P=30°,
故选C.

5.下列计算正确的是()
A.a2+a2=a4 B.(a2)3=a5 C.2a2﹣a2=2 D.a5•a2=a7
【考点】47:幂的乘方与积的乘方;35:合并同类项;46:同底数幂的乘法.
【分析】根据幂的乘方和积的乘方、合并同类项法则、同底数幂的乘法分别求出每个式子的值,再判断即可.
【解答】解:A、结果是2a2,故本选项不符合题意;
B、结果是a6,故本选项不符合题意;
C、结果是a2,故本选项不符合题意;
D、结果是a7,故本选项符合题意;
故选D.
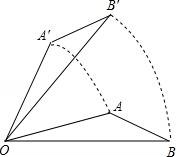
6.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是()
A.25° B.30° C.35° D.40°
【考点】R2:旋转的性质.
【分析】根据旋转的性质旋转前后图形全等以及对应边的夹角等于旋转角,进而得出答案即可.
【解答】解:∵将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,
∴∠A′OA=45°,∠AOB=∠A′OB′=15°,
∴∠AOB′=∠A′OA﹣∠A′OB′=45°﹣15°=30°,
故选:B.
7.下列命题是假命题的是()
A.若a>b,则ac2>bc2 B.若a>b,则a+c>b+c
C.若ac2>bc2,则a>b D.若a>b,b>c,则a>c
【考点】O1:命题与定理.
【分析】根据不等式的性质即可得到结论.
【解答】解:A、若a>b,且c≠0,则ac2>bc2,故错误;
B、若a>b,则a+c>b+c,故正确;
C、若ac2>bc2,则a>b,故正确;
D、若a>b,b>c,则a>c,故正确;
故选A.
8.一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【考点】X6:列表法与树状图法.
【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次都摸到白球的情况,再利用概率公式即可求得答案.
【解答】解:画树状图得:
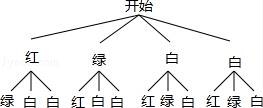
∵共有12种等可能的结果,两次都摸到白球的有2种情况,
∴两次都摸到白球的概率是:![]() =
=![]() .
.
故答案为:C.
9.如图,“凸轮”的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成.已知正三角形的边长为1,则凸轮的周长等于()

A.![]() B.
B.![]() C.π D.2π
C.π D.2π
【考点】MN:弧长的计算;KK:等边三角形的性质.
【分析】由“凸轮”的外围是以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成,得到∠A=∠B=∠C=60°,AB=AC=BC=1,然后根据弧长公式计算出三段弧长,三段弧长之和即为凸轮的周长.
【解答】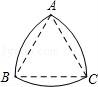
解:∵△ABC为正三角形,
∴∠A=∠B=∠C=60°,AB=AC=BC=1,
∴![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
根据题意可知凸轮的周长为三个弧长的和,
即凸轮的周长=![]() +
+![]() +
+![]() =3×
=3×![]() =π.
=π.
故选C.
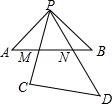
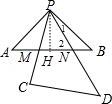
10.如图,将足够大的等腰直角三角板PCD的锐角顶点P放在另一个等腰直角三角板PAB的直角顶点处,三角板PCD绕点P在平面内转动,且∠CPD的两边始终与斜边AB相交,PC交AB于点M,PD交AB于点N,设AB=2,AN=x,BM=y,则能反映y与x的函数关系的图象大致是()
A.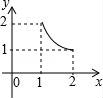 B.
B.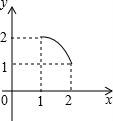 C.
C. D.
D.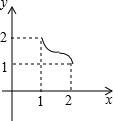
【考点】E7:动点问题的函数图象.
【分析】作PH⊥AB于H,根据等腰直角三角形的性质得∠A=∠B=45°,AH=BH=![]() AB=1,则可判断△PAH和△PBH都是等腰直角三角形,得到PA=PB=
AB=1,则可判断△PAH和△PBH都是等腰直角三角形,得到PA=PB=![]() AH=
AH=![]() ,∠HPB=45°,由于∠CPD的两边始终与斜边AB相交,PC交AB于点M,PD交AB于点N,而∠CPD=45°,所以1≤x≤2,再证明∠2=∠BPM,这样可判断△ANP∽△BPM,利用相似比得
,∠HPB=45°,由于∠CPD的两边始终与斜边AB相交,PC交AB于点M,PD交AB于点N,而∠CPD=45°,所以1≤x≤2,再证明∠2=∠BPM,这样可判断△ANP∽△BPM,利用相似比得![]() =
=![]() ,则y=
,则y=![]() ,所以得到y与x的函数关系的图象为反比例函数图象,且自变量为1≤x≤2.
,所以得到y与x的函数关系的图象为反比例函数图象,且自变量为1≤x≤2.
【解答】解:作PH⊥AB于H,如图,
∵△PAB为等腰直角三角形,
∴∠A=∠B=45°,AH=BH=![]() AB=1,
AB=1,
∴△PAH和△PBH都是等腰直角三角形,
∴PA=PB=![]() AH=
AH=![]() ,∠HPB=45°,
,∠HPB=45°,
∵∠CPD的两边始终与斜边AB相交,PC交AB于点M,PD交AB于点N,
而∠CPD=45°,
∴1≤AN≤2,即1≤x≤2,
∵∠2=∠1+∠B=∠1+45°,∠BPM=∠1+∠CPD=∠1+45°,
∴∠2=∠BPM,
而∠A=∠B,
∴△ANP∽△BPM,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴y=![]() ,
,
∴y与x的函数关系的图象为反比例函数图象,且自变量为1≤x≤2.
故选:A.
二、填空题(本大题6小题,每小题4分,共24分)
11.一个多边形的每一个外角都等于30°,则该多边形的内角和等于 1800° .
【考点】L3:多边形内角与外角.
【分析】多边形的外角和是360度,即可得到外角的个数,即多边形的边数.根据多边形的内角和定理即可求解.
【解答】解:多边形的边数是:![]() =12.
=12.
则内角和是:(12﹣2)•180=1800°
12.已知![]() +|a﹣b+2|=0,则ab= 1 .
+|a﹣b+2|=0,则ab= 1 .
【考点】23:非负数的性质:算术平方根;16:非负数的性质:绝对值.
【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.
【解答】解:由题意得,a+2=0,a﹣b+2=0,
解得a=﹣2,b=0,
所以,ab=(﹣2)0=1.
故答案为:1.
13.分解因式:﹣2a3+8a2﹣8a= ﹣2a(a﹣2)2 .
【考点】55:提公因式法与公式法的综合运用.
【分析】首先提取公因式,进而利用完全平方公式分解因式得出即可.
【解答】解:﹣2a3+8a2﹣8a
=﹣2a(a2﹣4a+4)
=﹣2a(a﹣2)2.
故答案为:﹣2a(a﹣2)2.
14.关于x的一元二次方程kx2﹣2x+1=0有两个不相等的实数根,则k的取值范围是 k<1且k≠0 .
【考点】AA:根的判别式;A1:一元二次方程的定义.
【分析】根据一元二次方程的定义和△的意义得到k≠0且△>0,即(﹣2)2﹣4×k×1>0,然后解不等式即可得到k的取值范围.
【解答】解:∵关于x的一元二次方程kx2﹣2x+1=0有两个不相等的实数根,
∴k≠0且△>0,即(﹣2)2﹣4×k×1>0,
解得k<1且k≠0.
∴k的取值范围为k<1且k≠0.
故答案为:k<1且k≠0.
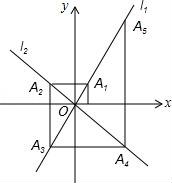
15.如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为.
【考点】F8:一次函数图象上点的坐标特征.
【分析】写出部分An点的坐标,根据坐标的变化找出变化规律“A2n+1((﹣2)n,2(﹣2)n)(n为自然数)”,依此规律即可得出结论.
【解答】解:观察,发现规律:A1(1,2),A2(﹣2,2),A3(﹣2,﹣4),A4(4,﹣4),A5(4,8),…,
∴A2n+1((﹣2)n,2(﹣2)n)(n为自然数).
∵2017=1008×2+1,
∴A2017的坐标为((﹣2)1008,2(﹣2)1008)=.
故答案为:.
16.如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC、BC为直径画半圆,则图中阴影部分的面积为 ![]() π﹣4 (结果保留π).
π﹣4 (结果保留π).
【考点】MO:扇形面积的计算.
【分析】图中阴影部分的面积为两个半圆的面积﹣三角形的面积,然后利用三角形的面积计算即可.
【解答】解: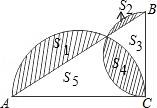
设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分的面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=![]() π×4+
π×4+![]() π×1﹣4×2÷2=
π×1﹣4×2÷2=![]() π﹣4.
π﹣4.
三、解答题(一)(本大题3小题,每小题6分,共18分)
17.计算:|1﹣![]() |﹣2sin45°+(
|﹣2sin45°+(![]() )﹣2+
)﹣2+![]() .
.
【考点】2C:实数的运算;6F:负整数指数幂;T5:特殊角的三角函数值.
【分析】原式利用绝对值的代数意义,特殊角的三角函数值,负整数指数幂法则,以及立方根定义计算即可得到结果.
【解答】解:原式=2![]() ﹣1﹣2×
﹣1﹣2×![]() +4﹣2=
+4﹣2=![]() +1.
+1.
18.先化简,再求值:(![]() ﹣
﹣![]() )÷
)÷![]() ,其中a=2,b=
,其中a=2,b=![]() .
.
【考点】6D:分式的化简求值.
【分析】首先将括号里面进行通分运算,进而利用分式除法运算法则计算得出答案.
【解答】解:原式=![]() ×
×![]()
=![]() ×
×![]()
=![]() ,
,
把a=2,b=![]() 代入可得:
代入可得:
原式=![]() =
=![]() =
=![]() =2+
=2+![]() .
.
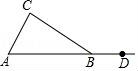
19. 如图,在△ABC中,AB=BC,点D在AB的延长线上.
(1)用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作∠CBD的平分线BM;
②作边BC上的中线AE,并延长AE交BM于点F.
(2)求证:BF∥AC.
【考点】N3:作图—复杂作图;KH:等腰三角形的性质.
【分析】(1)①作∠CBD的角平分线即可.②作线段BC的垂直平分线即可;
(2)只要证明∠DBF=∠CAB即可解决问题;
【解答】解:(1)①如图所示,BM即为所求.②如图所示,AF即为所求.
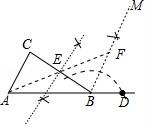
(2)∵BA=BC,
∴∠CAB=∠C,
∵∠CBD=∠C+∠CAB=∠CBF+∠DBF,∠CBF=∠DBF,
∴∠DBF=∠CAB,
∴BF∥AC.
四、解答题(二)(本大题3小题,每小题7分,共21分)
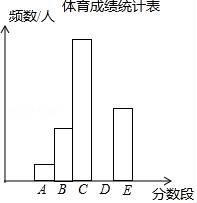
20. 为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计,得到统计图、表如图.
分数段 | A | B | C | D | E | 合计 |
频数/人 | 12 | 36 | 84 | b | 48 | c |
频率 | 0.05 | a | 0.35 | 0.25 | 0.20 | 1 |
根据上面的信息,回答下列问题:
(1)统计表中,a= 0.15 ,b= 60 ,c= 240 ;将频数分布直方图补充完整.
(2)小明说:“这组数据的众数一定在C中.”你认为小明的说法正确吗? 错误 (选填“正确”或“错误”).
(3)若成绩在27分及以上定为优秀,则该市30000名九年级学生中体育成绩为优秀的学生人数约有多少?
【考点】V8:频数(率)分布直方图;V5:用样本估计总体;V7:频数(率)分布表;W5:众数.
【分析】(1)首先用12÷0.05即可得到抽取的部分学生的总人数,然后用36除以总人数得到a,用总人数乘以0.25即可求出b;根据表格的信息就可以补全频数分布直方图;
(2)根据众数的定义和表格信息就可以得到这组数据的“众数”落在哪一组,进而判断小明的说法是否正确;
(3)利用30000乘以抽查的人数中优秀的学生人数所占的频率即可
【解答】解:(1)∵抽取的部分学生的总人数为c=12÷0.05=240(人),
∴a=36÷240=0.15,b=240×0.25=60;
统计图补充如下:
故答案是:0.15;60;240;
(2)C组数据范围是24.5~26.5,由于成绩均为整数,所以C组的成绩为25分与26分,虽然C组人数最多,但是25分与26分的人数不一定最多,所以这组数据的众数不一定在C中.故小明的说法错误;
故答案是:错误;
(3)30000×(0.25+0.20)=13500(人).
即该市今年30000名九年级学生中体育成绩为优秀的学生人数约有13500人.
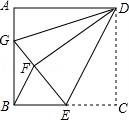
21.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.
(1)求证:AG=FG;
(2)求cos∠BGE的值.
【考点】PB:翻折变换(折叠问题);LE:正方形的性质;T7:解直角三角形.
【分析】(1)根据正方形的性质可得∠C=∠A=90°,DC=DA,根据翻折的性质可得DF=DC,∠DFE=∠C=90°,然后求出∠DFG=∠A=90°,DF=DA,再利用“HL”证明Rt△ADG和Rt△FDG全等,根据全等三角形对应边相等证明即可;
(2)先求出BE=EC=EF=6,设AG=x,表示出EG、BG,然后利用勾股定理列方程求出x的值,从而得到BG、EG,最后根据锐角的余弦等于邻边比斜边求解即可.
【解答】(1)证明:∵正方形ABCD,
∴∠C=∠A=90°,DC=DA,
∵△DCE沿DE对折得到△DFE,
∴DF=DC,∠DFE=∠C=90°,
∴∠DFG=∠A=90°,DF=DA,
在Rt△ADG和Rt△FDG中,![]() ,
,
∴Rt△ADG≌Rt△FDG(HL),
∴AG=FG;
(2)解:∵正方形ABCD中,AB=12,BE=EC,
∴BE=EC=EF=6,
设AG=x,则EG=6+x,
BG=12﹣x,
在Rt△BEG中,根据勾股定理得,EG2=BE2+BG2,
即(6+x)2=62+(12﹣x)2,
解得x=4,
所以,BG=12﹣4=8,
EG=6+4=10,
所以,cos∠BGE=![]() =
=![]() =
=![]() .
.
22.某商店第一次用600元购进某品牌的笔记本若干本,第二次又用600元购进同样品牌的笔记本,但这次每本的进价是第一次的1.25倍,购进数量比第一次少了30本.
(1)求第一次每本笔记本的进价是多少元?
(2)商店以同一价格全部销售完毕后获利不低于420元,问每本笔记本的售价至少多少元?
【考点】B7:分式方程的应用;C9:一元一次不等式的应用.
【分析】(1)设第一次每支铅笔进价为x元,则第二次每支铅笔进价为1.25x元,根据题意可列出分式方程解答;
(2)设售价为y元,求出利润表达式,然后列不等式解答.
【解答】解:(1)设第一次每本笔记本的进价为x元.
根据题意得![]() =
=![]() +30,
+30,
解得x=4,经检验x=4是原方程的解.
答:第一次每本笔记本的进价为4元;
(2)第一次买进笔记本150本,第二次买进笔记本120本,共270本.
设每本笔记本的售价为y元,根据题意得,
270y﹣600×2≥420,
解得y≥6.
答:每本笔记本的售价至少为6元.
五、解答题(三)(本大题3小题,每小题9分,共27分)
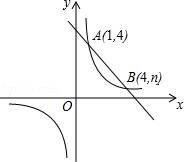
23.如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)直接写出关于x的不等式kx+b≤![]() 的解集.
的解集.
(3)点P是x轴上的一点,且使PA+PB最小,求△ABP的面积.
【考点】G8:反比例函数与一次函数的交点问题.
【分析】(1)将点A(1,4)代入反比例函数解析式可得其解析式;先根据反比例函数解析式求得点B坐标,再由A、B坐标可得直线解析式;
(2)根据图象得出不等式kx+b≤![]() 的解集即可;
的解集即可;
(3)作B的对称点B′,连接AB′,交x轴于P,此时PA+PB=AB′最小,根据B的坐标求得B′的坐标,然后根据待定系数法求得直线AB′的解析式,进而求得与x轴的交点P,再求面积即可.
【解答】解:(1)把A(1,4)代入y=![]() ,得:m=4,
,得:m=4,
∴反比例函数的解析式为y=![]() ;
;
把B(4,n)代入y=![]() ,得:n=1,
,得:n=1,
∴B(4,1),
把A(1,4)、(4,1)代入y=kx+b,得:![]() ,
,
解得:![]() ,
,
∴一次函数的解析式为y=﹣x+5;
(2)根据图象得当0<x≤1或x≥4,一次函数y=﹣x+5的图象在反比例函数y=![]() 的下方;
的下方;
∴kx+b≤![]() 的解集为0<x≤1或x≥4;
的解集为0<x≤1或x≥4;
(3)作B的对称点B′,连接AB′,交x轴于P,此时PA+PB=AB′最小,
∵B(4,1),
∴B′(4,﹣1),
设直线AB′的解析式为y=mx+n,
∴![]() ,
,
解得![]() ,
,
∴直线AB′的解析式为y=﹣![]() x+
x+![]() ,
,
令y=0,得﹣![]() x+
x+![]() =0,
=0,
解得x=![]() ,
,
∴点P的坐标为(![]() ,0),
,0),
∴S△ABP=![]() ﹣
﹣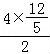
![]() =
=![]() .
.
24.如图1,⊙O是△ABC的外接圆,AB是直径,OD∥AC,OD交⊙O于点E,且∠CBD=∠COD.
(1)求证:BD是⊙O的切线;
(2)若点E为线段OD的中点,判断以O、A、C、E为顶点的四边形的形状并证明;
(3)如图2,作CF⊥AB于点F,连接AD交CF于点G,求![]() 的值.
的值.

【考点】MR:圆的综合题.
【分析】(1)由AB是⊙O的直径,根据直径所对的圆周角为直角得到∠BCA=90°,则∠ABC+∠BAC=90°,而∠CBD=∠BA,得到∠ABC+∠CBD=90°,即OB⊥BD,根据切线的判定定理即可得到BD为⊙O的切线;
(2)连接CE、BE,根据直角三角形斜边上的中线等于斜边的一半得到BE=OE=ED,则△OBE为等边三角形,于是∠BOE=60°,又因为AC∥OD,则∠OAC=60°,AC=OA=OE,即有AC∥OE且AC=OE,可得到四边形OACE是平行四边形,加上OA=OE,即可得到四边形OACE是菱形;
(3)由CF⊥AB得到∠AFC=∠OBD=90°,而AC∥OD,则∠CAF=∠DOB,根据相似三角形的判定易得Rt△AFC∽Rt△OBD,则有![]() =
=![]() ,即FC=
,即FC=![]() ,再由FG∥BD易证得△AFG∽△ABD,则
,再由FG∥BD易证得△AFG∽△ABD,则![]() =
=![]() ,即FG=
,即FG=![]() ,然后求FC与FG的比即可一个定值.
,然后求FC与FG的比即可一个定值.
【解答】(1)证明:如图1,∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠ABC+∠BAC=90°,
又∵∠CBD=∠BA,
∴∠ABC+∠CBD=90°,
∴∠ABD=90°,
∴OB⊥BD,
∴BD为⊙O的切线;
(2)证明:连接CE、BE,如图1,
∵OE=ED,∠OBD=90°,
∴BE=OE=ED,
∴△OBE为等边三角形,
∴∠BOE=60°,
又∵AC∥OD,
∴∠OAC=60°,
又∵OA=OC,
∴AC=OA=OE,
∴AC∥OE且AC=OE,
∴四边形OACE是平行四边形,
而OA=OE,
∴四边形OACE是菱形;
(3)解:如图2,∵CF⊥AB,
∴∠AFC=∠OBD=90°,
而AC∥OD,
∴∠CAF=∠DOB,
∴Rt△AFC∽Rt△OBD,
∴![]() =
=![]() ,即FC=
,即FC=![]() ,
,
又∵FG∥BD,
∴△AFG∽△ABD,
∴![]() =
=![]() ,即FG=
,即FG=![]() ,
,
∴![]() =
=![]() =2,
=2,
∴![]() =
=![]() .
.

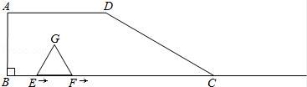
25.如图,四边形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°,点E、F同时从B点出发,沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG.设E点移动距离为x(0<x<6).
(1)点G在四边形ABCD的边上时,x= 2 ;点F与点C重合时,x= 3 ;
(2)求出使△DFC成为等腰三角形的x的值;
(3)求△EFG与四边形ABCD重叠部分的面积y与x之间的函数关系式,并直接写出y的最大值.

【考点】LO:四边形综合题.
【分析】(1)如图1中,作DH⊥BC于H,则四边形ABHD是矩形.当等边三角形△EGF的高=![]() 时,点G想AD上,此时x=2,当点F与C重合时,BE=
时,点G想AD上,此时x=2,当点F与C重合时,BE=![]() BC=3,此时x=3;
BC=3,此时x=3;
(2)分三种情形:①当CF=CD且F在C左侧时,当CF=CD且F在C右侧时,当FC=DF时,分别构建方程即可解决问题;
(3)分图1,图2,图3三种情形解决问题.①当0<x≤2时,如图1中,△EFG在四边形ABCD内部,重叠部分就是△EFG;
②当2<x<3时,如图2中,点E、F在线段BC上,△EFG与四边形ABCD重叠部分为四边形EFNM;
③当3≤x<6时,如图3中,点E在线段BC上,点F在射线BC上,重叠部分是△ECP;
【解答】解:(1)如图1中,作DH⊥BC于H,则四边形ABHD是矩形.

∵AD=BH=3,BC=6,
∴CH=BC﹣BH=3,
在Rt△DHC中,CH=3,∠DCH=30°,
∴DH=CH•tan30°=![]() ,
,
当等边三角形△EGF的高=![]() 时,点G想AD上,此时x=2,
时,点G想AD上,此时x=2,
当点F与C重合时,BE=![]() BC=3,此时x=3,
BC=3,此时x=3,
所以点G在四边形ABCD的边上时,x=2,点F与点C重合时,x=3.
故答案为2,3.
(2)注意到0<x<6,故△DFC为等腰三角形只有三种情形:
①当CF=CD且F在C左侧时,6﹣2x=2![]() ,x=3﹣
,x=3﹣![]() ,
,
②当CF=CD且F在C右侧时,2x﹣6=2![]() ,x=3+
,x=3+![]() ,
,
③当FC=DF时,6﹣2x=![]() ,x=
,x=![]() ,
,
综上所述,x的值为3﹣![]() 或3+
或3+![]() 或
或![]() .
.
(3)①当0<x≤2时,如图1中,△EFG在四边形ABCD内部,所以y=![]() x2.
x2.
②当2<x<3时,如图2中,点E、F在线段BC上,△EFG与四边形ABCD重叠部分为四边形EFNM,
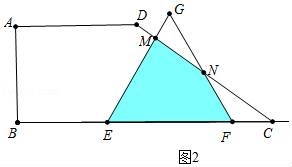
∵∠FNC=∠FCN=30°,
∴FN=FC=6﹣2x,
∴GN=3x﹣6,
∵∠G=60°,
∴△GNM是直角三角形,
∴y=S△EFG﹣S△GMN=![]() x2﹣
x2﹣![]() (3x﹣6)2=﹣
(3x﹣6)2=﹣![]() x2+
x2+![]() x﹣
x﹣![]() .
.
③当3≤x<6时,如图3中,点E在线段BC上,点F在射线BC上,重叠部分是△ECP,

y=![]() (6﹣x)2=
(6﹣x)2=![]() x2﹣
x2﹣![]() x+
x+![]() .
.
2017年8月16日

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...