2017年广东省惠州市惠阳区中考数学模拟试卷题【精编解析版】
由于版式的问题,试题可能会出现乱码的现象,为了方便您的阅读请点击全屏查看
一.选择题(共10小题,每小题3分,共30分.)
1.![]() 的倒数是()
的倒数是()
A.﹣2 B.2 C.![]() D.
D.![]()
2.下列图案中既是中心对称图形,又是轴对称图形的是()
A.![]() B.
B. C.
C. D.
D.
3.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为()
A.44×108 B.4.4×109 C.4.4×108 D.4.4×1010
4.2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是()
A.32,31 B.31,32 C.31,31 D.32,35
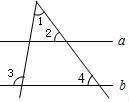
5.如图,直线a∥b,若∠2=55°,∠3=100°,则∠1的度数为()
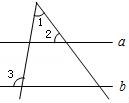
A.35° B.45° C.50° D.55°
6.下列运算正确的是()
A.2a+3b=5ab B.a2•a3=a5 C.(2a)3=6a 3 D.a6+a3=a9
7.一元二次方程x2﹣4x+2=0的根的情况是()
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
8.若等腰三角形的两边长为3和7,则该等腰三角形的周长为()
A.10 B.13 C.17 D.13或17
9.不等式组![]() 的解集在数轴上表示正确的是()
的解集在数轴上表示正确的是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是()

A. B.
B.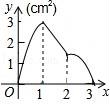 C.
C.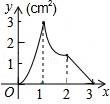 D.
D.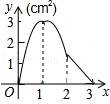
二、填空题(本题共6小题,每小题4分,共24分)
11.因式分解:x2﹣36= .
12.一个多边形的内角和为1080°,则这个多边形的边数是 .
13.若△ABC∽△A′B′C′,相似比为1:3,则△ABC与△A′B′C′的面积之比为 .
14.分式方程![]() 的解是 .
的解是 .
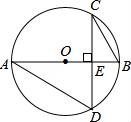
15.如图,在⊙O中,CD⊥AB于E,若∠BAD=30°,且BE=2,则CD= .
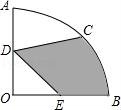
16.如图,在圆心角为90°的扇形OAB中,半径OA=4,C为![]() 的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为 .
的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为 .
三、解答题(本题共3小题,每小题6分,共18分)
17.计算:(﹣![]() )﹣1﹣|
)﹣1﹣|![]() ﹣1|+3tan30°+0.
﹣1|+3tan30°+0.
18.先化简,再求值:
(![]() )
)![]() ,请在﹣3,0,1,3中选择一个适当的数作为x值.
,请在﹣3,0,1,3中选择一个适当的数作为x值.
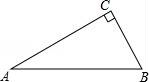
19.如图,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明)
(2)连接BD,求证:DE=CD.
四、解答题(本题共3小题,每小题7分,共21分)
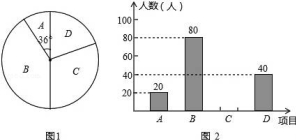
20.某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图补充完成;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
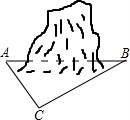
21.为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,![]() ≈1.73,精确到个位)
≈1.73,精确到个位)
22.某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?
五、解答题(本题共3小题,每小题9分,共27分)
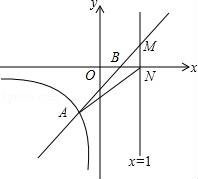
23.直线y=kx+b与反比例函数y=![]() (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN=![]() ,求t的值.
,求t的值.
24.已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EH•EA;
(3)若⊙O的半径为5,sinA=![]() ,求BH的长.
,求BH的长.

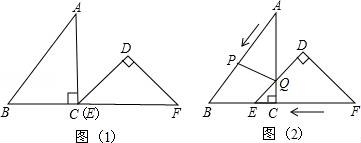
25.把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合),点B、C(E)、F在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=10cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以2cm/s的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s).
(1)用含t的代数式表示线段AP和AQ的长,并写出t的取值范围;
(2)连接PE,设四边形APEQ的面积为y(cm2),试探究y的最大值;
(3)当t为何值时,△APQ是等腰三角形.
2017年广东省惠州市惠阳区中考数学模拟试卷题参考答案与试题解析
一.选择题(共10小题,每小题3分,共30分.)
1.![]() 的倒数是()
的倒数是()
A.﹣2 B.2 C.![]() D.
D.![]()
【考点】17:倒数.
【分析】根据倒数的定义求解.
【解答】解:﹣![]() 的倒数是﹣2.
的倒数是﹣2.
故选:A.
2.下列图案中既是中心对称图形,又是轴对称图形的是()
A.![]() B.
B. C.
C. D.
D.
【考点】R5:中心对称图形;P3:轴对称图形.
【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.
【解答】解:A、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;
B、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确;
C、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误;
D、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故此选项错误.
故选:B.
3.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为()
A.44×108 B.4.4×109 C.4.4×108 D.4.4×1010
【考点】1I:科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:4 400 000 000=4.4×109,
故选:B.
4.2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是()
A.32,31 B.31,32 C.31,31 D.32,35
【考点】W5:众数;W4:中位数.
【分析】利用中位数及众数的定义确定答案即可.
【解答】解:∵数据31出现了3次,最多,
∴众数为31,
∵排序后位于中间位置的数是31,
∴中位数是31,
故选C.
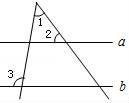
5.如图,直线a∥b,若∠2=55°,∠3=100°,则∠1的度数为()
A.35° B.45° C.50° D.55°
【考点】JA:平行线的性质.
【分析】根据两直线平行,同位角相等可得∠4=∠2,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
【解答】解:如图,∵直线a∥b,
∴∠4=∠2=55°,
∴∠1=∠3﹣∠4=100°﹣55°=45°.
故选B.
6.下列运算正确的是()
A.2a+3b=5ab B.a2•a3=a5 C.(2a)3=6a 3 D.a6+a3=a9
【考点】47:幂的乘方与积的乘方;35:合并同类项;46:同底数幂的乘法.
【分析】直接利用合并同类项法则以及结合幂的乘方与积的乘方法则,分别化简求出答案.
【解答】解:A、2a+3b无法计算,故此选项不合题意;
B、a2•a3=a5,正确,符合题意;
C、(2a)3=8a 3,故此选项不合题意;
D、a6+a3,无法计算,故此选项不合题意;
故选:B.
7.一元二次方程x2﹣4x+2=0的根的情况是()
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
【考点】AA:根的判别式.
【分析】先计算出判别式的值,然后根据判别式的意义判定方程解的情况.
【解答】解:∵△=(﹣4)2﹣4×2=8>0,
∴方程有两个不相等的实数根.
故选A.
8.若等腰三角形的两边长为3和7,则该等腰三角形的周长为()
A.10 B.13 C.17 D.13或17
【考点】KH:等腰三角形的性质;K6:三角形三边关系.
【分析】因为等腰三角形的两边为3和7,但已知中没有点明底边和腰,所以有两种情况,需要分类讨论,还要注意利用三角形三边关系考查各情况能否构成三角形.
【解答】解:当3为底时,其它两边都为7,3、7、7可以构成三角形,周长为17;
当3为腰时,其它两边为3和7,
∵3+3=6<7,
所以不能构成三角形,故舍去,
∴答案只有17.
故选C.
9.不等式组![]() 的解集在数轴上表示正确的是()
的解集在数轴上表示正确的是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【考点】C4:在数轴上表示不等式的解集;CB:解一元一次不等式组.
【分析】先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
【解答】解:由x>﹣1,得x>﹣1,
由2x≤4,得x≤2,
∴不等式组的解集是﹣1<x≤2,
故选:B.
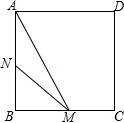
10.如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是()
A.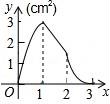 B.
B. C.
C.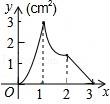 D.
D.
【考点】E7:动点问题的函数图象.
【分析】分三种情况进行讨论,当0≤x≤1时,当1≤x≤2时,当2≤x≤3时,分别求得△ANM的面积,列出函数解析式,根据函数图象进行判断即可.
【解答】解:由题可得,BN=x,
当0≤x≤1时,M在BC边上,BM=3x,AN=3﹣x,则
S△ANM=![]() AN•BM,
AN•BM,
∴y=![]() •(3﹣x)•3x=﹣
•(3﹣x)•3x=﹣![]() x2+
x2+![]() x,故C选项错误;
x,故C选项错误;
当1≤x≤2时,M点在CD边上,则
S△ANM=![]() AN•BC,
AN•BC,
∴y=![]() (3﹣x)•3=﹣
(3﹣x)•3=﹣![]() x+
x+![]() ,故D选项错误;
,故D选项错误;
当2≤x≤3时,M在AD边上,AM=9﹣3x,
∴S△ANM=![]() AM•AN,
AM•AN,
∴y=![]() •(9﹣3x)•(3﹣x)=
•(9﹣3x)•(3﹣x)=![]() (x﹣3)2,故B选项错误;
(x﹣3)2,故B选项错误;
故选(A).
二、填空题(本题共6小题,每小题4分,共24分)
11.因式分解:x2﹣36= (x+6)(x﹣6) .
【考点】54:因式分解﹣运用公式法.
【分析】直接用平方差公式分解.平方差公式:a2﹣b2=(a+b)(a﹣b).
【解答】解:x2﹣36=(x+6)(x﹣6).
12.一个多边形的内角和为1080°,则这个多边形的边数是 8 .
【考点】L3:多边形内角与外角.
【分析】n边形的内角和是(n﹣2)•180°,如果已知多边形的边数,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.
【解答】解:根据n边形的内角和公式,得
(n﹣2)•180=1080,
解得n=8.
∴这个多边形的边数是8.
故答案为:8.
13.若△ABC∽△A′B′C′,相似比为1:3,则△ABC与△A′B′C′的面积之比为 1:9 .
【考点】S7:相似三角形的性质.
【分析】根据相似三角形面积的比等于相似比的平方解答.
【解答】解:∵△ABC∽△A′B′C′,相似比为1:3,
∴△ABC与△A′B′C′的面积之比为1:9.
故答案为:1:9.
14.分式方程![]() 的解是 x=﹣1 .
的解是 x=﹣1 .
【考点】B2:分式方程的解.
【分析】根据解分式方程的方法可以求得分式方程![]() 的解,记住最后要进行检验,本题得以解决.
的解,记住最后要进行检验,本题得以解决.
【解答】解:![]()
方程两边同乘以2x(x﹣3),得
x﹣3=4x
解得,x=﹣1,
检验:当x=﹣1时,2x(x﹣3)≠0,
故原分式方程的解是x=﹣1,
故答案为:x=﹣1.
15.如图,在⊙O中,CD⊥AB于E,若∠BAD=30°,且BE=2,则CD= 4![]() .
.

【考点】M2:垂径定理;M5:圆周角定理.
【分析】先根据圆周角定理求出∠C的度数,再由CD⊥AB可知∠CEB=90°,CD=2CE,由直角三角形的性质求出BC的长,根据勾股定理求出CE的长,进而可得出结论.
【解答】解:∵∠BAD=30°,BE=2,
∴∠C=∠BAD=30°.
∵CD⊥AB,
∴∠CEB=90°,CD=2CE,
∴BC=2BE=4,
∴CE=![]() =
=![]() =2
=2![]() ,
,
∴CD=2CE=4![]() .
.
故答案为:4![]() .
.
16.如图,在圆心角为90°的扇形OAB中,半径OA=4,C为![]() 的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为 2π+2
的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为 2π+2![]() ﹣2 .
﹣2 .
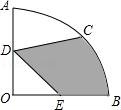
【考点】MO:扇形面积的计算.
【分析】连接OC、EC,由△OCD≌△OCE、OC⊥DE可得DE=![]() =2
=2![]() ,分别求出S扇形OBC、S△OCD、S△ODE面积,根据S扇形OBC+S△OCD﹣S△ODE=S阴影部分可得.
,分别求出S扇形OBC、S△OCD、S△ODE面积,根据S扇形OBC+S△OCD﹣S△ODE=S阴影部分可得.
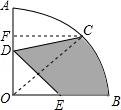
【解答】解:连结OC,过C点作CF⊥OA于F,
∵半径OA=4,C为![]() 的中点,D、E分别是OA、OB的中点,
的中点,D、E分别是OA、OB的中点,
∴OD=OE=2,OC=4,∠AOC=45°,
∴CF=2![]() ,
,
∴空白图形ACD的面积=扇形OAC的面积﹣三角形OCD的面积
=![]() ﹣
﹣![]() ×2×2
×2×2![]()
=2π﹣2![]() ,
,
三角形ODE的面积=![]() OD×OE=2,
OD×OE=2,
∴图中阴影部分的面积=扇形OAB的面积﹣空白图形ACD的面积﹣三角形ODE的面积
=![]() ﹣(2π﹣2
﹣(2π﹣2![]() )﹣2
)﹣2
=2π+2![]() ﹣2.
﹣2.
故答案为:2π+2![]() ﹣2.
﹣2.
三、解答题(本题共3小题,每小题6分,共18分)
17.计算:(﹣![]() )﹣1﹣|﹣1|+3tan30°+0.
)﹣1﹣|﹣1|+3tan30°+0.
【考点】2C:实数的运算;6E:零指数幂;6F:负整数指数幂;T5:特殊角的三角函数值.
【分析】原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及特殊角的三角函数值计算即可得到结果.
【解答】解:原式=﹣4﹣![]() +1+3×
+1+3×![]() +1=﹣2.
+1=﹣2.
18.先化简,再求值:
(![]() )
)![]() ,请在﹣3,0,1,3中选择一个适当的数作为x值.
,请在﹣3,0,1,3中选择一个适当的数作为x值.
【考点】6D:分式的化简求值.
【分析】先把括号内通分,再把分子分母因式分解和除法运算化为乘法运算,然后约分得到原式=3x+15,再根据分式有意义的条件把x=1代入计算即可.
【解答】解:原式=![]() •
•![]()
=![]() •
•![]()
=3x+15,
当x=1时,原式=3+15=18.
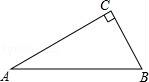
19.如图,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明)
(2)连接BD,求证:DE=CD.
【考点】N2:作图—基本作图;KG:线段垂直平分线的性质;KO:含30度角的直角三角形.
【分析】(1)利用基本作图(作已知线段的垂直平分线)作DE垂直平分AB;
(2)先利用线段垂直平分线的性质得到DA=DB,则∠DBA=∠A=30°,再证明BD平分∠ABC,然后根据角平分线的性质定理可得到结论.
【解答】(1)解:如图,DE为所作;
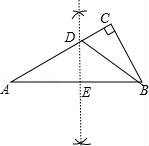
(2)证明:如图,
∵DE垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=30°,
∵∠ABC=90°﹣∠A=60°,
∴∠CBD=30°,
即BD平分∠ABC,
而DE⊥AB,DC⊥BC,
∴DE=DC.
四、解答题(本题共3小题,每小题7分,共21分)
20.某学校为了增强学生体质,决定开设以下体育课外活动项目:A篮球、B乒乓球、C跳绳、D踢毽子,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 200 人;
(2)请你将条形统计图补充完成;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
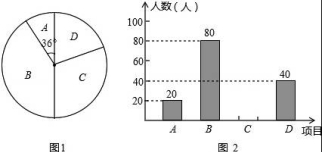
【考点】X6:列表法与树状图法;VB:扇形统计图;VC:条形统计图.
【分析】(1)由题意可知这次被调查的学生共有20÷![]() =200(人);
=200(人);
(2)首先求得C项目对应人数为:200﹣20﹣80﹣40=60(人),继而可补全条形统计图;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中甲、乙两位同学的情况,再利用概率公式即可求得答案.
【解答】解:(1)根据题意得:这次被调查的学生共有20÷![]() =200(人).
=200(人).
故答案为:200;
(2)C项目对应人数为:200﹣20﹣80﹣40=60(人);
补充如图.
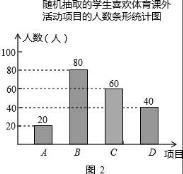
(3)列表如下:
| 甲 | 乙 | 丙 | 丁 |
甲 | ﹨ | (乙,甲) | (丙,甲) | (丁,甲) |
乙 | (甲,乙) | ﹨ | (丙,乙) | (丁,乙) |
丙 | (甲,丙) | (乙,丙) | ﹨ | (丁,丙) |
丁 | (甲,丁) | (乙,丁) | (丙,丁) | ﹨ |
∵共有12种等可能的情况,恰好选中甲、乙两位同学的有2种,
∴P(选中甲、乙)=![]() =
=![]() .
.
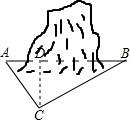
21.为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,![]() ≈1.73,精确到个位)
≈1.73,精确到个位)
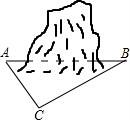
【考点】T8:解直角三角形的应用.
【分析】首先过点C作CD⊥AB于D,然后在Rt△BCD中,利用三角函数的知识,求得BD,CD的长,继而在Rt△ACD中,利用∠CAB的正切求得AD的长,继而求得答案.
【解答】解:过点C作CD⊥AB于D,
∵BC=200m,∠CBA=30°,
∴在Rt△BCD中,CD=![]() BC=100m,BD=BC•cos30°=200×
BC=100m,BD=BC•cos30°=200×![]() =100
=100![]() ≈173(m),
≈173(m),
∵∠CAB=54°,
在Rt△ACD中,AD=![]() ≈
≈![]() ≈72(m),
≈72(m),
∴AB=AD+BD=173+72≈245(m).
答:隧道AB的长为245m.
22.某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?
【考点】AD:一元二次方程的应用;C9:一元一次不等式的应用.
【分析】(1)设该种商品每次降价的百分率为x%,根据“两次降价后的售价=原价×(1﹣降价百分比)的平方”,即可得出关于x的一元二次方程,解方程即可得出结论;
(2)设第一次降价后售出该种商品m件,则第二次降价后售出该种商品件,根据“总利润=第一次降价后的单件利润×销售数量+第二次降价后的单件利润×销售数量”,即可得出关于m的一元一次不等式,解不等式即可得出结论.
【解答】解:(1)设该种商品每次降价的百分率为x%,
依题意得:400×(1﹣x%)2=324,
解得:x=10,或x=190(舍去).
答:该种商品每次降价的百分率为10%.
(2)设第一次降价后售出该种商品m件,则第二次降价后售出该种商品件,
第一次降价后的单件利润为:400×(1﹣10%)﹣300=60(元/件);
第二次降价后的单件利润为:324﹣300=24(元/件).
依题意得:60m+24×=36m+2400≥3210,
解得:m≥22.5.
∴m≥23.
答:为使两次降价销售的总利润不少于3210元.第一次降价后至少要售出该种商品23件.
五、解答题(本题共3小题,每小题9分,共27分)
23.直线y=kx+b与反比例函数y=![]() (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN=![]() ,求t的值.
,求t的值.

【考点】G8:反比例函数与一次函数的交点问题.
【分析】(1)将点A坐标代入y=![]() 可得m的值;
可得m的值;
(2)将点A、B坐标代入y=kx+b可得关于k、b的方程,解方程求出k、b的值,可得直线解析式;
(3)根据直线直线x=t与直线y=kx+b交于点M、与x轴交于点N表示出M、N的坐标,由S△AMN=![]() 可得关于t的方程,解方程可得t的值.
可得关于t的方程,解方程可得t的值.
【解答】解:(1)将点A(﹣1,m)代入y=![]() ,得:m=﹣2;
,得:m=﹣2;
(2)由(1)知点A坐标为(﹣1,﹣2),
将点A(﹣1,﹣2)、B(1,0)代入y=kx+b,
得:![]() ,
,
解得:![]() ,
,
∴直线AB的解析式为:y=x﹣1;
(3)当x=t时,y=t﹣1,
∴点M坐标为(t,t﹣1),点N坐标为(t,0),
∵S△AMN=![]() ,
,
∴![]() ×(t﹣1)(t+1)=
×(t﹣1)(t+1)=![]() ,
,
解得:t=2或t=﹣2(舍),
∴t=2.
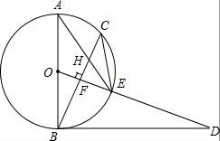
24.已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EH•EA;
(3)若⊙O的半径为5,sinA=![]() ,求BH的长.
,求BH的长.
【考点】MR:圆的综合题.
【分析】(1)由圆周角定理和已知条件证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;
(2)连接AC,由垂径定理得出![]() ,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例
,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例![]() ,即可得出结论;
,即可得出结论;
(3)连接BE,由圆周角定理得出∠AEB=90°,由三角函数求出BE,再根据勾股定理求出EA,得出BE=CE=6,由(2)的结论求出EH,然后根据勾股定理求出BH即可.
【解答】(1)证明:∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,
即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线;
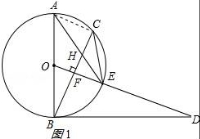
(2)证明:连接AC,如图1所示:
∵OF⊥BC,
∴![]() ,
,
∴∠CAE=∠ECB,
∵∠CEA=∠HEC,
∴△CEH∽△AEC,
∴![]() ,
,
∴CE2=EH•EA;
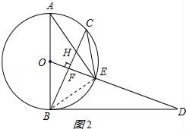
(3)解:连接BE,如图2所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵⊙O的半径为5,sin∠BAE=![]() ,
,
∴AB=10,BE=AB•sin∠BAE=10×![]() =6,
=6,
∴EA=![]() =
=![]() =8,
=8,
∵![]() ,
,
∴BE=CE=6,
∵CE2=EH•EA,
∴EH=![]() =
=![]() ,
,
在Rt△BEH中,BH=![]() =
=![]() =
=![]() .
.
25.把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合),点B、C(E)、F在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=10cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以2cm/s的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s).
(1)用含t的代数式表示线段AP和AQ的长,并写出t的取值范围;
(2)连接PE,设四边形APEQ的面积为y(cm2),试探究y的最大值;
(3)当t为何值时,△APQ是等腰三角形.

【考点】S9:相似三角形的判定与性质;H7:二次函数的最值;KH:等腰三角形的性质.
【分析】(1)根据题意以及直角三角形性质表达出CQ、AQ,从而得出结论,
(2)作PG⊥x轴,将四边形的面积表示为S△ABC﹣S△BPE﹣S△QCE即可求解,
(3)根据题意以及三角形相似对边比例性质即可得出结论.
【解答】(1)解:AP=2t
∵∠EDF=90°,∠DEF=45°,
∴∠CQE=45°=∠DEF,
∴CQ=CE=t,
∴AQ=8﹣t,
t的取值范围是:0≤t≤5;
(2)过点P作PG⊥x轴于G,可求得AB=10,SinB=![]() ,PB=10﹣2t,EB=6﹣t,
,PB=10﹣2t,EB=6﹣t,
∴PG=PBSinB=![]() (10﹣2t)
(10﹣2t)
∴y=S△ABC﹣S△PBE﹣S△QCE=![]() =
=![]()
∴当![]() (在0≤t≤5内),y有最大值,y最大值=
(在0≤t≤5内),y有最大值,y最大值=![]() (cm2)
(cm2)

(3)若AP=AQ,则有2t=8﹣t解得:![]() (s)
(s)
若AP=PQ,如图①:过点P作PH⊥AC,则AH=QH=![]() ,PH∥BC
,PH∥BC
∴△APH∽△ABC,
∴![]() ,
,
即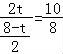 ,
,
解得:![]() (s)
(s)
若AQ=PQ,如图②:过点Q作QI⊥AB,则AI=PI=![]() AP=t
AP=t
∵∠AIQ=∠ACB=90°∠A=∠A,
∴△AQI∽△ABC
∴![]() 即
即![]() ,
,
解得:![]() (s)
(s)
综上所述,当![]() 或
或![]() 或
或![]() 时,△APQ是等腰三角形.
时,△APQ是等腰三角形.

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...