2017-2018肇庆鼎湖中学九年级第一次月考数学试题【word版无答案】
由于版式的问题,试题可能会出现乱码的现象,为了方便您的阅读请点击全屏查看
(满分120分,考试时间100分钟)
一、选择题(本大题共10小题,每小题3分,共30分)
1、下列方程中,是关于x的一元二次方![]() 程为()
程为()
A. ![]() B.
B.![]()
C. x2-5=0 ![]() D.
D.![]() 2、方程x2=6x的根是( )
2、方程x2=6x的根是( )
A、x1=0,x2=-6 B、x1=0,x2=6C、x=6 D、x=0
3、抛物线![]() 的顶点坐标是()
的顶点坐标是()
A.(2,1) B.(-2,1) C.(2,-1) D.(-2,-1)
4. 已知方程![]() ,则下列说中,正确的是( )
,则下列说中,正确的是( )
(A)方程两根和是1 (B)方程两根积是2
(C)方程两根和是![]() (D)方程两根积比两根和大2
(D)方程两根积比两根和大2
5. 二次函数y=x2的图象向右平移3个单位,得到新的图象的函数表达式是()
A. y=x2+3 B. y=x2-3 C. y=(x+3)2 D. y=(x-3)2
6、把方程![]() 化为一元二次方程的一般形式是(
化为一元二次方程的一般形式是( ![]() )
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7.为执行“两免一补”政策,某地区![]() 2015年投入教育经费2500万元,预计2017年投入3600万元.设这两年投入教育经费的年平均增长率为
2015年投入教育经费2500万元,预计2017年投入3600万元.设这两年投入教育经费的年平均增长率为![]() ,则下列方程正确的是()#网A.
,则下列方程正确的是()#网A.![]() B.
B.![]()
C.2500(1+x)=3600 D.![]()
8.已知二次函数![]() 的图象经过原点
的图象经过原点![]() ,则
,则![]() 的值为()
的值为()
 A. 0或2 B. 0 C. 2D.无法确定
A. 0或2 B. 0 C. 2D.无法确定
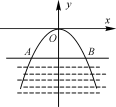
9. 如图所示的桥拱是抛物线形,其函数的表达式为y=-x2,当
水位线在AB位置时,水面宽12 m,这时水面离桥顶的高度为()
A.3 m B.2 m C.4 m D.9 m
10、![]() 已知一个直角三角形的两条直角边的长恰好是方程
已知一个直角三角形的两条直角边的长恰好是方程![]() 的两个根,则这个直角三角形的斜边长是()
的两个根,则这个直角三角形的斜边长是()
A、![]() B、3 C
B、3 C![]() 、6
、6![]() D、9
D、9
二、填空题(本大题共6小题,每![]() 小题4分,共24分)
小题4分,共24分)
11、方程![]() 的根是 .
的根是 .
12、若x2-kx+4是一个完全平方式,则k= .
13、 已知x=1是关于x的一元二次方程2x2 + kx-1=0的一个根,则实数k= .
14、将方程x2-![]() 4x-1=0化为(x-m)2=n的形式,其中m,n是常数,则m+n=.
4x-1=0化为(x-m)2=n的形式,其中m,n是常数,则m+n=.
15、若点A(2,m)在抛物线y=x2上,则点A关于y轴对称点的坐标是
![]()
 16、设a、b是方程
16、设a、b是方程![]() 的两个不等的根,则a2+2a+b的值为________.
的两个不等的根,则a2+2a+b的值为________.
解答题:(本大题共3小题,每![]() 小题6分,共18分)
小题6分,共18分)
17、 x2+10x+9 =0 18、![]()
19.已知抛物线的顶点(-1,-2)且图象经过(1,10),求此抛物线解析式。
四.解答题:(本大题共3小题,每![]() 小题7分,共21分)
小题7分,共21分)
20、已知:x1,x2是关于x的方程x2+(2a-1)x+a2=0的两个实数根且(x1+2)(x2+2)=11![]() ,求a的值.
,求a的值.
21.用配方法把二次函数y=x2-4x+7化成y=a(x-h)2+k的形式,并写出该函数图象的开口方向、对称轴和顶点坐标.
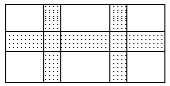
22.如图所示,在宽为20m,长为32m的矩形耕地上,修筑同样宽的三条道路,(互相垂直),把耕地分成大小不等的六块试验田,要使试验田的面积为570m2,道路应为多宽?
五.解![]() 答题:(本大题共3小题,每
答题:(本大题共3小题,每![]() 小题9分,共27分)
小题9分,共27分)
23.已知一次函数y=ax+b的图象上有两点A、B,它们的横坐标分别是3,-1,若二次函数y=![]() x2的图象经过A、B两点.(1)请求出一次函数的表达式;(2)设二次函数的顶点为C,求△ABC的面积.
x2的图象经过A、B两点.(1)请求出一次函数的表达式;(2)设二次函数的顶点为C,求△ABC的面积.
![]() 24、某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经
24、某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经![]()
![]() 调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。 求:(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?(2)每件衬衫降价多少元时,商场平均每天赢利最多?
调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。 求:(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?(2)每件衬衫降价多少元时,商场平均每天赢利最多?
25.如图,A,![]() B,C,D
B,C,D![]() 为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
为矩形的四个顶点,AB=16 cm,AD=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
(1)P,Q两点从出发开始到几秒时,四边形PBCQ的面积为33 cm2?
(2)P,Q两点从出发开始到几秒时,点P和点Q之间的距离是10 cm?
【解析】∵x1,x2是方程x2+(2a![]() -1)x+a2=0的两个实数根,∴x1+x2=1-2a,x1·x2=a2,
-1)x+a2=0的两个实数根,∴x1+x2=1-2a,x1·x2=a2,
∵(x1+2)(x2+2)=11,∴x1x2+2(x1+x2)+4=11,∴a2+2(1-2a)-7=0,即a2-4a-5=0,
解得a=-1或a=5.又∵Δ=(2a-1)2-4a2=1-4a≥0,∴a≤![]() .
.
∴a=5不合题意,舍去.∴a=-1.
25.⑴解:设每件衬衫应降价x元。(40-x)(20+2x)=1200
800![]() +80x-20x-2x2-1200=0x2-30x+200
+80x-20x-2x2-1200=0x2-30x+200![]() =0(x-10)(x-20)=0x1=10(
=0(x-10)(x-20)=0x1=10(![]() 舍去) x2=20
舍去) x2=20
⑵解:设每件衬衫降价x元时,则所得赢利为(40-x)(20+2x)=-2 x2+60x+800[来源:]=-2(x2-30x+225)+1250=-2(x-15)2+1250
所以,每件衬衫降价15元时,商场赢利最多,为1250元。
24.解:(1)设P,Q两点从出发开始到x s时,四边形PBCQ的面积为33 cm2,则AP=3x cm,CQ=2x cm,所以PB=(16-3x)cm.因为(PB+CQ)×BC×=33,所以(16-3x+2x)×6×=33.解得x=5,所以P,Q两点从出发开始到5 s时,四边形PBCQ的面积为33 cm2.
(2)![]() 设P,Q两点从出发开始到a s时
设P,Q两点从出发开始到a s时![]() ,点P和点Q之间的距离是10 cm.
,点P和点Q之间的距离是10 cm.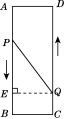
如图,过点Q作QE⊥AB于E,易得EB=QC,EQ=BC=6 cm,
所以PE=|PB-BE|=|PB-QC|=|16-3a-2a|=|16-5a|(cm).
在Rt△PEQ中,PE2+EQ2=PQ2,所以(16-5a)2+62=102,即25a2-160a+192=0,解得a1=,a2![]() =,所以P,Q两点从出发开始到 s或 s时,点P和点Q之间的距离是10 cm.
=,所以P,Q两点从出发开始到 s或 s时,点P和点Q之间的距离是10 cm.
22、解:设道路宽为xm
(32-2x)(20-x)=570
640-32x-40x+2x2=570
x2-36x+35=0
(x-1)(x-35)=0
x1=1 x2=35(舍去)
答:道路应宽1m

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...