2016-2017学年广东省汕头市潮南区七年级(下)期末数学试题【含答案】
由于版式的问题,试题可能会出现乱码的现象,为了方便您的阅读请点击全屏查看
一、选择題(每小题3分,共30分)
1.下列实数是无理数的是()
A.![]() B.
B.![]() C.﹣
C.﹣![]() D.0
D.0
2.如图,与∠1是同旁内角的是()
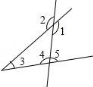
A.∠2 B.∠3 C.∠4 D.∠5
3.下列运动属于平移的是()
A.冷水加热过程中小气泡上升成为大气泡
B.投篮时的篮球运动
C.急刹车时汽车在地面上的滑动
D.随风飘动的树叶在空中的运动
4.如图,能判定EB∥AC的条件是()
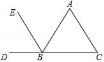
A.∠A=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠C=∠ABE
5.某不等式组的解集在数轴上表示如图所示,则这个不等式组可能是()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知点P(2﹣a,3)到两坐标轴距离相等,则a的值为()
A.3 B.﹣1 C.﹣1 或 5 D.﹣3
7.已知![]() 是方程2mx﹣y=10的解,则m的值为()
是方程2mx﹣y=10的解,则m的值为()
A.2 B.4 C.6 D.10
8.如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数()
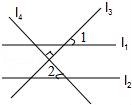
A.46° B.44° C.36° D.22°
9.在平面直角坐标系中,若点A (a,﹣b)在第一象限内,则点B (a,b﹣3)所在的象限是()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.关于x的不等式组![]() 的解集为x>1,则a的取值范围是()
的解集为x>1,则a的取值范围是()
A.a>1 B.a<1 C.a≥1 D.a≤1
二、填空题(每小题4分,共24分)
11.在平面直角坐标系中,点(﹣4,4)在第 象限.
12.要了解5000件商品的质量问题,从中任意抽取40件商品进行试验,在这个问题中,样本容量是 .
13.某正数的平方根是n+l和n﹣5,则这个数为 .
14.如图,C岛在A岛的北偏东60°方向,在B岛的北偏西45°方向,则∠ACB= .
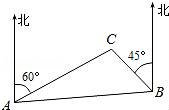
15.不等式5x﹣3<3x+5的最大整数解是 .
16.已知(3x+2y﹣5)2与|4x﹣2y﹣9|互为相反数,则xy= .
三、解答題(一)(每小题6分,共18分)
17.计算:﹣12017﹣![]() +
+![]() .
.
18.x取哪些非负整数时,![]() 的值大于
的值大于![]() 与1的差.
与1的差.
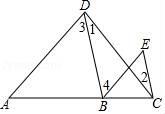
19.已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.
四、解答题(二)(每小题7分,共21分)
20.解方程组![]() .
.
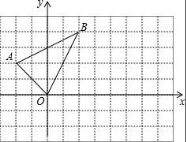
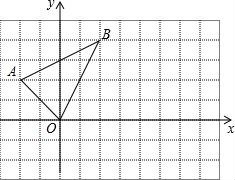
21.如图:
(1)将△ABO向右平移4个单位,请画出平移后的三角形A'B'O',并写出点A'、B'的坐标.
(2)求△ABO的面积.
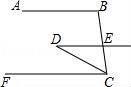
22.如果AB∥CF,DE∥CF,∠DCB=40°,∠D=30°,求∠B的度数.
五、解答题(三)(每小题9分,共27分)
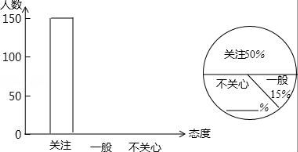
23.为了了解市民对“汕头市创建全国文明城市”的态度,某一天,小明等同学在本市的甲、乙和丙三个村的村民进行了一次随机调査,结果如图表:
村民态度 | 甲村 | 乙村 | 丙村 | 合计 |
关注 | 20 | 75 | 55 | 150 |
一般 | 23 | 5 | 17 | 45 |
不关心 | 57 | 20 | 28 | 105 |
(1)请将频数分布直方图补充完整;
(2)此次共调查了多少人?并求出一般在扇形统计图中所占圆心角的度数.
(3)用您学过的统计知识来说明哪个村的调査结果更能反映市民对“创文”的态度,请写出一句“创文”的宣传语.
24.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.

25.暑期中,哥哥和弟弟二人分别编织28个中国结,已知弟弟单独编织一周(7天)不能完成,而哥哥单独编织不到一周就已完成.哥哥平均每天比弟弟多编2个.
求:(1)哥哥和弟弟平均每天各编多少个中国结?(答案取整数)
(2)若弟弟先工作2天,哥哥才开始工作,那么哥哥工作几天,两人所编中国结数量相同?
2016-2017学年广东省汕头市潮南区七年级(下)期末数学试题参考答案与试题解析
一、选择題(每小题3分,共30分)
1.下列实数是无理数的是()
A.![]() B.
B.![]() C.﹣
C.﹣![]() D.0
D.0
【考点】26:无理数.
【分析】根据无理数、有理数的定义即可判定选择项.
【解答】解:![]() ,
,![]() ,0是有理数,
,0是有理数,
﹣![]() 是无理数,
是无理数,
故选:C.
2.如图,与∠1是同旁内角的是()
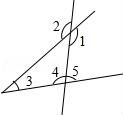
A.∠2 B.∠3 C.∠4 D.∠5
【考点】J6:同位角、内错角、同旁内角.
【分析】根据同位角、内错角、同旁内角、对顶角的定义逐个判断即可.
【解答】解:A、∠1和∠2是对顶角,不是同旁内角,故本选项错误;
B、∠1和∠3是同位角,不是同旁内角,故本选项错误;
C、∠1和∠4是内错角,不是同旁内角,故本选项错误;
D、∠1和∠5是同旁内角,故本选项正确;
故选D.
3.下列运动属于平移的是()
A.冷水加热过程中小气泡上升成为大气泡
B.投篮时的篮球运动
C.急刹车时汽车在地面上的滑动
D.随风飘动的树叶在空中的运动
【考点】Q1:生活中的平移现象.
【分析】根据平移的定义,对选项进行一一分析,排除错误答案.
【解答】解:A、冷水加热过程中小气泡上升成为大气泡有大小变化,不符合平移定义,故错误;
B、投篮时的篮球不沿直线运动,故错误;
C、急刹车时汽车在地面上的滑动是平移,故正确;
D、随风飘动的树叶在空中不沿直线运动,故错误.
故选:C.
4.如图,能判定EB∥AC的条件是()
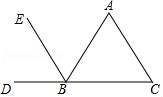
A.∠A=∠ABE B.∠A=∠EBD C.∠C=∠ABC D.∠C=∠ABE
【考点】J9:平行线的判定.
【分析】在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线.
【解答】解:A、∠A=∠ABE,根据内错角相等,两直线平行,可以得出EB∥AC,故本选项正确.
B、∠A=∠EBD不能判断出EB∥AC,故本选项错误;
C、BC、∠C=∠ABC只能判断出AB=AC,不能判断出EB∥AC,故本选项错误;
D、∠C=∠ABE不能判断出EB∥AC,故本选项错误;
故选:A.
5.某不等式组的解集在数轴上表示如图所示,则这个不等式组可能是()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【考点】CB:解一元一次不等式组;C4:在数轴上表示不等式的解集.
【分析】先根据数轴得出不等式组的解集,再求出每个选项中不等式组的解集,即可得出答案.
【解答】解:从数轴可知:不等式组的解集为﹣1≤x<4,
A、不等式组的解集为空集,故本选项不符合题意;
B、不等式组的解集为﹣1≤x<4,故本选项符合题意;
C、不等式组的解集为x>4,故本选项不符合题意;
D、不等式组的解集为﹣1<x≤4,故本选项不符合题意;
故选B.
6.已知点P(2﹣a,3)到两坐标轴距离相等,则a的值为()
A.3 B.﹣1 C.﹣1 或 5 D.﹣3
【考点】D1:点的坐标.
【分析】根据到两坐标的距离相等,可得关于a的方程,根据解方程,可得答案.
【解答】解:由题意,得
2﹣a=3或2﹣a=﹣3,
解得a=﹣1或a=5,
故选:C.
7.已知![]() 是方程2mx﹣y=10的解,则m的值为()
是方程2mx﹣y=10的解,则m的值为()
A.2 B.4 C.6 D.10
【考点】92:二元一次方程的解;86:解一元一次方程.
【分析】把x=1,y=2代入方程得到一个关于m的方程,求出方程的解即可
【解答】解:把x=1,y=2代入方程2mx﹣y=10得:2m﹣2=10,
解得:m=6,
故选:C.
8.如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数()
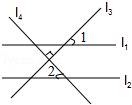
A.46° B.44° C.36° D.22°
【考点】JA:平行线的性质.
【分析】由l1∥l2,可得:∠1=∠3=44°,由l3⊥l4,可得:∠2+∠3=90°,进而可得∠2的度数.
【解答】解:如图,
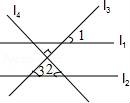
∵l1∥l2,
∴∠1=∠3=44°,
∵l3⊥l4,
∴∠2+∠3=90°,
∴∠2=90°﹣44°=46°.
故选:A.
9.在平面直角坐标系中,若点A (a,﹣b)在第一象限内,则点B (a,b﹣3)所在的象限是()
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】D1:点的坐标.
【分析】根据各象限内点的坐标特征解答即可.
【解答】解:由题意,得
a>0,﹣b>0,
b<0.
b﹣3<﹣3,
点B (a,b﹣3)所在的象限是第四象限,
故选:D.
10.关于x的不等式组![]() 的解集为x>1,则a的取值范围是()
的解集为x>1,则a的取值范围是()
A.a>1 B.a<1 C.a≥1 D.a≤1
【考点】C3:不等式的解集.
【分析】解两个不等式后,根据其解集得出关于a的不等式,解答即可.
【解答】解:因为不等式组![]() 的解集为x>1,
的解集为x>1,
所以可得a≤1,
故选D
二、填空题(每小题4分,共24分)
11.在平面直角坐标系中,点(﹣4,4)在第 二 象限.
【考点】D1:点的坐标.
【分析】根据各象限内点的坐标特征解答.
【解答】解:点(﹣4,4)在第二象限.
故答案为:二.
12.要了解5000件商品的质量问题,从中任意抽取40件商品进行试验,在这个问题中,样本容量是 40 .
【考点】V3:总体、个体、样本、样本容量.
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【解答】解:要了解5000件商品的质量问题,从中任意抽取40件商品进行试验,在这个问题中,样本容量是40,
故答案为:40.
13.某正数的平方根是n+l和n﹣5,则这个数为 9 .
【考点】21:平方根.
【分析】依据正数的两个平方根互为相反数求解即可.
【解答】解:∵某正数的平方根是n+l和n﹣5,
∴n+1+n﹣5=0,解得n=2.
∴这个正数=32=9.
故答案为:9.
14.如图,C岛在A岛的北偏东60°方向,在B岛的北偏西45°方向,则∠ACB= 105° .
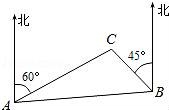
【考点】IH:方向角.
【分析】过点C作CD∥AE,从而可证明CD∥BF,然后由平行线的性质可知∠DCA=∠CAE,∠DCB=∠CBF,从而可求得∠ACB的度数.
【解答】解:过点C作CD∥AE.
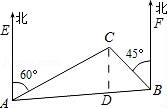
∵CD∥AE,BF∥AE,
∴CD∥BF.
∵CD∥AE,
∴∠DCA=∠CAE=60°,
同理:∠DCB=∠CBF=45°.
∴∠ACB=∠ACD+∠BCD=105°.
15.不等式5x﹣3<3x+5的最大整数解是 3 .
【考点】C7:一元一次不等式的整数解.
【分析】首先利用不等式的基本性质解不等式,再从不等式的解集中找出适合条件的正整数即可.
【解答】解:不等式的解集是x<4,
故不等式5x﹣3<3x+5的正整数解为1,2,3,
则最大整数解为3.
故答案为:3.
16.已知(3x+2y﹣5)2与|4x﹣2y﹣9|互为相反数,则xy= ﹣1 .
【考点】98:解二元一次方程组;16:非负数的性质:绝对值;1F:非负数的性质:偶次方.
【分析】利用非负数的性质列出方程组,求出方程组的解得到x与y的值,即可求出xy的值.
【解答】解:∵(3x+2y﹣5)2与|4x﹣2y﹣9|互为相反数,
∴(3x+2y﹣5)2+|4x﹣2y﹣9|=0,
∴![]() ,
,
①+②得:7x=14,
解得:x=2,
把x=2代入①得:y=﹣![]() ,
,
则xy=﹣1,
故答案为:﹣1
三、解答題(一)(每小题6分,共18分)
17.计算:﹣12017﹣![]() +
+![]() .
.
【考点】2C:实数的运算.
【分析】首先计算乘方、开方,然后从左向右依次计算,求出算式的值是多少即可.
【解答】解:﹣12017﹣![]() +
+![]()
=﹣1+2+5
=6
18.x取哪些非负整数时,![]() 的值大于
的值大于![]() 与1的差.
与1的差.
【考点】C7:一元一次不等式的整数解.
【分析】根据题意列出不等式,解不等式后再求出x的非负整数值.
【解答】解:由题意得:![]() >
>![]() ﹣1,解得x<4,
﹣1,解得x<4,
∴x取0,1,2,3.
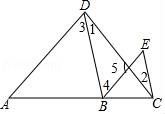
19.已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.
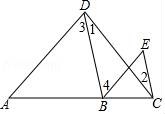
【考点】J9:平行线的判定.
【分析】先根据题意得出∠1+∠3=∠2+∠E,再由∠2+∠E=∠5可知,∠1+∠3=∠5,即∠ADC=∠5,据此可得出结论.
【解答】证明:∵∠1=∠2,∠3=∠E,
∴∠1+∠3=∠2+∠E.
∵∠2+∠E=∠5,
∴∠1+∠3=∠5,
∴∠ADC=∠5,
∴AD∥BE.
四、解答题(二)(每小题7分,共21分)
20.解方程组![]() .
.
【考点】98:解二元一次方程组.
【分析】方程组利用加减消元法求出解即可.
【解答】解:![]() ,
,
②×2,得2x﹣4y=8③,
由①﹣③得7y=﹣7,即y=﹣1,
把y=﹣1代入②中,得x+2=4,即x=2,
则方程组的解为![]() .
.
21.如图:
(1)将△ABO向右平移4个单位,请画出平移后的三角形A'B'O',并写出点A'、B'的坐标.
(2)求△ABO的面积.
【考点】Q4:作图﹣平移变换.
【分析】(1)画出A、B、O三点平移后的对应点A′、B′、O′即可解决问题;
(2)利用分割法求三角形的面积即可;
【解答】解:(1)平移后的三角形A'B'O',如图所示.A′(2,2),B′(6,4).
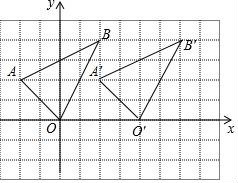
(2)S△AOB=4×4﹣![]() ×2×4﹣
×2×4﹣![]() ×2×2﹣
×2×2﹣![]() ×2×4=16﹣4﹣2﹣4=6.
×2×4=16﹣4﹣2﹣4=6.
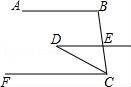
22.如果AB∥CF,DE∥CF,∠DCB=40°,∠D=30°,求∠B的度数.
【考点】JA:平行线的性质.
【分析】根据平行线的性质即可得到结论.
【解答】解:∵DE∥CF,∠D=30°,
∴∠DCF=∠D=30°,
∴∠BCF=∠DCF+∠BCD=30°+40°=70°,
又∵AB∥CF,
∴∠B+∠BCF=180°,
∴∠B=180°﹣70°=110°.
五、解答题(三)(每小题9分,共27分)
23.为了了解市民对“汕头市创建全国文明城市”的态度,某一天,小明等同学在本市的甲、乙和丙三个村的村民进行了一次随机调査,结果如图表:
村民态度 | 甲村 | 乙村 | 丙村 | 合计 |
关注 | 20 | 75 | 55 | 150 |
一般 | 23 | 5 | 17 | 45 |
不关心 | 57 | 20 | 28 | 105 |
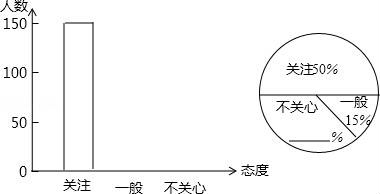
(1)请将频数分布直方图补充完整;
(2)此次共调查了多少人?并求出一般在扇形统计图中所占圆心角的度数.
(3)用您学过的统计知识来说明哪个村的调査结果更能反映市民对“创文”的态度,请写出一句“创文”的宣传语.
【考点】V8:频数(率)分布直方图;VB:扇形统计图.
【分析】(1)根据统计表中的数据可以将直方图补充完整;
(2)根据统计表中的数据可以求得本次调查的总人数,由扇形统计图可以求得一般在扇形统计图中所占圆心角的度数;
(3)根据统计图中的数据可以得到哪个村的调査结果更能反映市民对“创文”的态度,对于宣传语只要积极向上合理即可.
【解答】解:(1)补全的频数分布直方图,如右图所示;
(2)由题意可得,
此次调查的人有:150+45+105=300(人),
一般在扇形统计图中所占圆心角的度数是:360°×15%=54°;
(3)由统计图可以看出乙村反映市民对“创文”的态度比较积极,
“创文”的宣传语是:创文与我们每个人息息相关,让我大家一起携手共创文明城市.
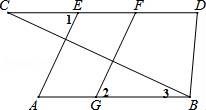
24.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠D=∠3+60°,∠CBD=70°.
(1)求证:AB∥CD;
(2)求∠C的度数.
【考点】JB:平行线的判定与性质.
【分析】(1)求出AE∥GF,求出∠2=∠A=∠1,根据平行线的判定推出即可;
(2)根据平行线的性质得出∠D+∠CBD+∠3=180°,求出∠3,根据平行线的性质求出∠C即可.
【解答】(1)证明:∵AE⊥BC,FG⊥BC,
∴AE∥GF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠A,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠D+∠CBD+∠3=180°,
∵∠D=∠3+60°,∠CBD=70°,
∴∠3=25°,
∵AB∥CD,
∴∠C=∠3=25°.
25.暑期中,哥哥和弟弟二人分别编织28个中国结,已知弟弟单独编织一周(7天)不能完成,而哥哥单独编织不到一周就已完成.哥哥平均每天比弟弟多编2个.
求:(1)哥哥和弟弟平均每天各编多少个中国结?(答案取整数)
(2)若弟弟先工作2天,哥哥才开始工作,那么哥哥工作几天,两人所编中国结数量相同?
【考点】CE:一元一次不等式组的应用;8A:一元一次方程的应用.
【分析】(1)设弟弟每天编x个中国结,根据弟弟单独工作一周(7天)不能完成,得7x<28;根据哥哥单独工作不到一周就已完成,得7(x+2)>28,列不等式组进行求解;
(2)设哥哥工作m天,两人所编中国结数量相同,结合(1)中求得的结果,列方程求解.
【解答】解:(1)设弟弟每天编x个中国结,则哥哥每天编(x+2)个中国结.
依题意得:![]() ,
,
解得:2<x<4.
∵x取正整数,
∴x=3;x+2=5,
答:弟弟每天编3个中国结,哥哥每天编5个中国结.
(2)设哥哥工作m天,两人所编中国结数量相同,
依题意得:3(m+2)=5m,
解得:m=3.
答:弟弟每天编3个中国结;若弟弟先工作2天,哥哥才开始工作,那么哥哥工作3天,两人所编中国结数量相同.
2017年7月21日

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...