2017-2018年深圳九年级期中联考数学试题【word版含答案】

2017-2018年深圳九年级期中联考数学试题【word版含答案】

由于版式的问题，试题可能会出现乱码的现象，为了方便您的阅读请点击全屏查看

一．选择题（每小题3分，共36分）

1．方程（x﹣1）（x﹣2）=2的根是（）

A．x1=1，x2=2              B．x1=﹣1，x2=﹣2              C．x=3   D．x1=0，x2=3             

2．下列各组中的四条线段成比例的是（）

A．a=，b=3，c=2，d=              B．a=4，b=6，c=5，d=10

C．a=2，b=，c=2，d=              D．a=2，b=3，c=4，d=1

3．如图所示几何体的左视图是（）

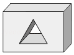
A．              B．              C．              D．

4．下列命题正确的个数有（）

①两边成比例且有一角对应相等的两个三角形相似；②对角线相等的四边形是矩形；

③任意四边形的四边中点连接所形成的四边形是平行四边形；

④两个相似多边形的面积比为2：3，则周长比为4：9．

A．1个              B．2个              C．3个              D．4个

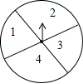
5．如图，转盘中四个扇形的面积都相等．小明随意转动转盘2次，

当转盘停止转动时，二次指针所指向数字的积为偶数的概率为（）

A．              B．              C．              D．

6．如图，在△ABC中，若DE∥BC，AD=5，BD=10，DE=4，则BC的值为（）

A．8              B．9              C．10              D．12

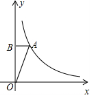7．如图，反比例函数y＝(k≠0)的图象上有一点A，AB平行于x轴

交y轴于点B，△ABO的面积是1，则反比例函数的解析式是（）

A.  y＝        B. y＝

C. y＝         D. y＝

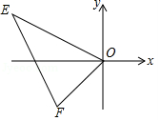8．如在平面直角坐标系中，已知点E（﹣4，2），F（﹣2，﹣2）．若△OE′F′与△OEF关于点O位似，且S△OE′F′：S△OEF=1：4，则点E′的坐标为（）

A．（2，﹣1）              B．（8，﹣4）             

C．（2，﹣1）或（﹣2，1）              D．（8，﹣4）或（﹣8，4）

9．如图所示，在一边靠墙（墙足够长）空地上，修建一个面积为672m2的矩形临时仓库，仓库一边靠墙另三边用总长为76 m的栅栏围成，若设栅栏AB的长为xm，则下列各方程中，符合题意的是（）

A．x（76﹣x）=672              B．x（76﹣2x）=672

C．x（76﹣2x）=672              D．x（76﹣x）=672

10．如图，在直角三角形ABC中，∠C=90°，在底边AB上方位

置有边长分别为3，4，x的三个相邻的正方形，则x的值为（）

A．5              B．6              C．7              D．12

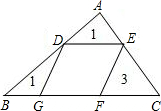
11．如图，平行四边形DEFG内接于△ABC，已知△ADE，△EFC，

△DBG的面积为1，3，1，那么□DEFG的面积为（）

A．3              B．4              C．5              D．6

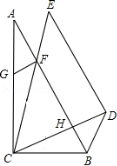
12．如图，Rt△ABC和Rt△CDE中，∠A=30°，∠E=45°，AB=CE

，∠BCD=30°，FG⊥AB，下列结论：①CH=FH；②BC=GC；

③四边形BDEF为平行四边形；④FH=GF+BH．其中正确的结论是（）

A．①②③              B．①②④              C．①③④              D．①②③④

二．填空题（每小题3分，共12分）

13．方程2x﹣4=0的解也是关于x的方程x2+mx+2=0的一个解，则m的值为　   　．

14．把一袋黑豆中放入100粒黄豆，搅匀后取出100粒豆子，其中有黄豆4粒，则该袋中约有黑豆　   　．

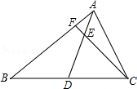15．如图，AD是△ABC的中线，E是AD上的一点，且AE=AD，CE

交AB于点F。若AF=1.2cm，则AB=　   　cm．

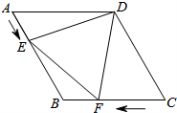16．如图，在菱形ABCD中，AB=4cm，∠ADC=120°，点E，F同时由A，C两点出发，分别沿AB，CB方向向点B匀速移动（到点B为止），点E的速度为1cm/s，点F的速度为2cm/s，经过t秒△DEF为等边三角形，则t的值为   　

三．解答题（共52分）

17. （9分）解方程：

（1）x2+4x+2=0

（2）3x2+2x﹣1=0；

（3）（2x+1）2=﹣3（2x+1）

18.（6分）某商场为了吸引顾客，设计了一种促销活动．在一个不透明的箱子里放有4个完全相同的小球，球上分别标有“0元”、“10元”、“30元”和“50元”的字样．规定：顾客在本商场同一日内，消费每满300元，就可以从箱子里先后摸出两个球（每次只摸出一个球，第一次摸出后不放回）．商场根据两个小球所标金额之和返还相应价格的购物券，可以重新在本商场消费．某顾客消费刚好满300元，则在本次消费中：

（1）该顾客至少可得　   　元购物券，至多可得　   　元购物券；（2分）

（2）请用画树状图或列表法，求出该顾客所获购物券的金额不低于50元的概率．（4分）

19.（6分）如图，小军、小珠所在位置A,B之间的距离为2.8m，小军、小珠在同一盏路灯P下的影长分别为1.2m，1.5m，已知小军、小珠的身高分别为1.8m，1.5m，

(1)画出两人在路灯下的影子AC和BD;（2分）

(2)求路灯的高PO．（4分）

20.（7分）如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．

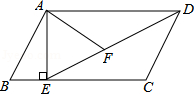（1）求证：△ADF∽△DEC；（3分）

（2）若AB=8，AD=6，AF=4，求AE的长．（4分）

21.（7分）西瓜经营户以 2 元/千克的价格购进一批小型西瓜，以 3 元/千克的价格出售，每天可售出 200 千克.为了促销，该经营户决定降价销售.经调查发现，这种 小型西瓜每降价 0.1 元/千克，每天可多售出 40 千克.另外，每天的房租等固定成本 共 24 元.

（1）若将这种西瓜每千克的售价降低x元，则每天的销售量是　   　千克（用含x的代数式表示）；（1分）

（2）销售这种水果要想每天盈利200元且使每天的销售量较大，需将每千克的售价降低多少元？（6分）

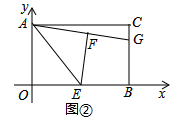
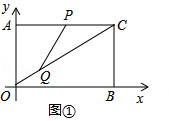
22.（8分）如图，在平面直角坐标系中，矩形AOBC的边长为AO=6，BO=8，如图①，动点P以每秒2个单位的速度由点C向点A沿线段CA运动，同时点Q以每秒4个单位的速度由点O向点C沿线段OC运动。

（1）用含t的代数式表示：CP=         ，QC=         （2分）

（2）在运动过程中， P、Q、C三点是否能构成等腰三角形，若能，请求出点P的坐标．（3分）

（3）如图②，E是OB的中点，将△AOE沿AE折叠后得到△AFE，点F在矩形AOBC内部，延长AF交BC于点G．求点G的坐标．（3分）

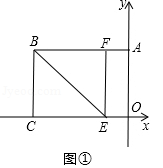
23.（9分）如图①，矩形OABC的边OA、OC分别在坐标轴上，点B在第二象限，且点B的横、纵坐标是一元二次方程m2+m﹣12=0的两个实数根．把矩形OABC沿直线BE折叠，使点C落在AB边上的点F处，点E在CO边上．

（1）直接填空：B（，），F（，）；（2分）

（2）如图②，若△BCE从该位置开始，以固定的速度沿x轴水平向右移动，平移的距离记为a．记△BCE平移后为△B′C′E′，当a为何值时△B′C′E′与△BEF重合部分为菱形？（3分）

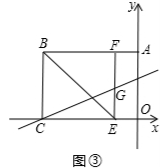
（3）如图③，设点G为EF中点，若点M在直线CG上，点N在y轴上，是否存在这样的点M，使得以M、N、B、G为顶点的四边形为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由。（4分）

2017-2018年深圳九年级期中联考数学试题参考答案

一、选择题：

二、填空题：

13、  -3      14、  2400          15、 6            16、

三、解答题：

17、解：（1）x2+4x+2=0

移项，得：x2+4x=﹣2，

配方，得：x2+4x+4=﹣2+4，……………………1分

即（x+2）2=2，………………………………………..2分

解这个方程，得：x+2=±；

即x1=-2+，x2=-2﹣．………….……………3分

（2）3x2+2x﹣1=0；

这里a=3，b=2，c=﹣1，

∵△=4+12=16，……………………1分

∴x=，……………………2分

∴x1=，x2=﹣1．……………………3分

（3）（2x+1）2=﹣3（2x+1）

（2x+1）2+3（2x+1）=0，

（2x+1）[（2x+1）+3]=0，……………………1分

（2x+1）（2x+4）=0，……………………2分

解得：x1=﹣，x2=﹣2．……………………3分 (其它方法参考给分)

18、（1）  10 ，   80   ……………………2分

（2）列表得：

∵两次摸球可能出现的结果共有12种，每种结果出现的可能性相同，而所获购物券的金额不低于50元的结果共有6种．                     ……………………5分

∴该顾客所获购物券的金额不低于50元的概率是：．……………………6分

19、解：(1)  如图，AC,BD即为所求。…………………2分

(2)如图，∵AE∥PO∥BF，

∴△AEC∽△POC，△BFD∽△OPD，…………………3分

∴，，

即，，

解得：PO=3.3m．…………………5分

答：路灯的高为3.3m．…………………6分

20、证明：∵四边形ABCD是平行四边形，

∴AB∥CD，AD∥BC，

∴∠B+∠C=180°，∠ADF=∠DEC．…………………1分

∵∠AFD+∠AFE=180°，∠AFE=∠B

∴∠AFD=∠C…………………2分

∴△ADF∽△DEC；…………………3分

（2）解：∵四边形ABCD是平行四边形，

∴CD=AB=4，由（1）知△ADF∽△DEC，

∴，…………………4分

∴DE=12…………………6分

在Rt△ADE中，由勾股定理得：

==6．…………7分

21、解：（1）200+400x　…………………1分

（2）设应将每千克小型西瓜的售价降低x元，根据题意，得

[（3-2）-x]（200+-24=200

可化为：50x2-25x+3=0，…………………4分
解这个方程，得x1=0.2，x2=0.3．…………………6分

为使每天的销量较大，应降价0.3元，即定价3-0.3=2.7元/千克．
答：应将每千克小型西瓜的售价定为2.7元/千克．…………………7分

22、解：（1）2t，10﹣4t…………………2分

（2）设运动的时间为t秒，

由勾股定理得，OC==10，

1）当CQ=CP时，2t=10﹣4t，解得，t=，

此时CP=2×=，∴AP=8﹣=，

P点坐标为（，6）…………………3分

2）当PC=PQ时，

如图①，过点p作OC的垂线交OC于点E，CQ=10﹣4t，CP=2t．

CE==5-2t

易证△CEP∽△CAO，

∴，即：

解得  t=

∴P点坐标为（，6），…………………4分

3）当QC=PQ时，如图②，过点Q作AC的垂线交AC于点F，

CQ=10﹣4t，CP=2t，CF=t

∵△CFQ∽△CAO，

∴，即：

∴t=

则P点坐标为（，6），

综上所述，P点坐标为（，6），（，6），（，6）；…………………5分

（3）如图③，连接EG，

由题意得：△AOE≌△AFE，

∴∠EFG=∠OBC=90°，

∵E是OB的中点，∴EG=EG，EF=EB=4，

在Rt△EFG和Rt△EBG中，

，

∴Rt△EFG≌Rt△EBG（HL）……………6分

∴∠3=∠4

∵∠1+∠2+∠3+∠4=180°，∠1=∠2   ∴∠2+∠3=90°，可证△AOE∽△EBG。……………7分

∴，即：

∴ BG=，G的坐标为（8，）．…………………8分

23、解：（1）（﹣4，3），（﹣1，3）；………………2分

（2）△B′C′E′与四边形OABE重叠部分是四边形B′GEM，

∵B′E′//BE ,  B′C′//EF

∴四边形B′GEM为平行四边形。当B′G=B′M时，平行四边形B′GEM为菱形。

由折叠得∠B′BG=∠FB′M=45°

则BB′=a,B′G=a  ,BF=3-a  ,FM=3-a  B′M=a

在Rt△B′FM中，由勾股定理得 (3-a)2+(3-a)2=a2

解得a1=         a2=（舍去）

∴当a=时重合部分为菱形。           ……………5分

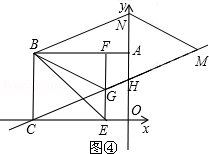（3）存在。设MG的解析式为：y=kx+b，

把C（﹣4，0），G（﹣1，1.5）代入得：，

解得：，∴CG：y=0.5x+2……………6分

1)如图④，N在y轴正半轴，且BG为其中一边。

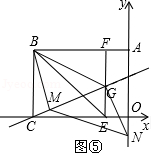由题知 B(-4,3)，G(-1，)，N(0,y)

由BN//GM且BN=BM得：XM  =0+3=3

代入得 y M= 3.5

∴   M1（3，3.5）……………7分

2) 如图⑤ N在y轴负半轴，且BG为其中一边。

由BN//GM且BN=BM得：XM  =0-3=-3

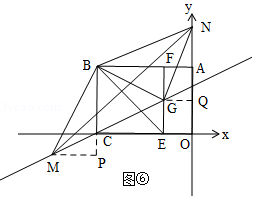代入得 y M= 0.5∴   M2（-3，0.5）……………8分

3）如图⑥当BG为对角线时，

由题知 B(-4,3)，G(-1，)，N(0,y)

X M  =-5  代入得 y M= ﹣

符合条件的点M的坐标为（3，3.5）、（﹣3，0.5）、（﹣5，﹣）．

……………9分