机密★启用前
各位同学在查看时请点击全屏查看
2018年遵义中考数学模拟试题
(全卷总分150分,考试时间120分钟)
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
5.考试结束后,将试题卷和答题卡一并交回。
一、选择题(本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符号题目要求的,请用2B铅笔把答题卡上对应题目的答案标号涂黑、涂满。)
 1.-3的相反数是
1.-3的相反数是
A.-3 B.![]() C.
C.![]() D.3
D.3
2.如图,梯子的各条横档互相平行,若∠1=![]() ,则∠2的度数是
,则∠2的度数是
A. B.![]() C.
C.![]() D.
D.![]()
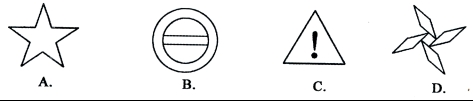
3.下列图形中既是中心对称图形,又是轴对称图形的是
4.计算![]() 的结果是
的结果是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.不等式![]() ≤0的解集在数轴上表示为
≤0的解集在数轴上表示为

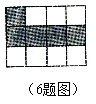 6.如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是
6.如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是
一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂
上阴影,能构成这个正方体的表面展开图的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 7.函数
7.函数![]() 的自变量
的自变量![]() 的取值范围是
的取值范围是
A.![]() >-2 B.
>-2 B.![]() <2 C.
<2 C.![]() ≠2 D.
≠2 D.![]() ≠-2
≠-2
8.一组数据2、1、5、4的方差是
A.10 B.3 C.2.5 D.0.75
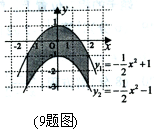
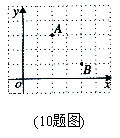 9.如图,两条抛物线
9.如图,两条抛物线![]() 、
、![]() 与分别经过点
与分别经过点![]() ,
,![]() 且平行于
且平行于![]() 轴的两条平行线围成的阴影部分的面积为
轴的两条平行线围成的阴影部分的面积为
A.8 B.6 C.10 D.4
10.在一次 “寻宝”游戏中,“寻宝”人找到了如图所标示的两个标志
点A![]() 、B
、B![]() ,A、B两点到“宝藏”点的距离都是
,A、B两点到“宝藏”点的距离都是![]() ,则
,则
“宝藏”点的坐标是
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
二、填空题(本题共8小题,每小题4分,共32分。答题请用0.5毫米黑色墨水的签字笔或钢笔直接答在答题卡的相应位置上。)
11.太阳半径约为696000千米,数字696000用科学记数法表示为 ▲ .
12.分解因式: ![]() = ▲ .
= ▲ .
13.如图,△ABC内接于⊙O,∠C=![]() ,则∠ABO= ▲ 度.
,则∠ABO= ▲ 度.
14.如图,已知正方形的边长为![]() ,以对角的两个顶点为圆心,
,以对角的两个顶点为圆心, ![]() 长为半径画弧,则所得到的两条弧的长度之和为 ▲
长为半径画弧,则所得到的两条弧的长度之和为 ▲ ![]() (结果保留
(结果保留![]() ).
).
15.如图,在宽为![]() ,长为
,长为![]() 的矩形地面上修建两条宽都是
的矩形地面上修建两条宽都是![]() 的道路,余下部分种植花草.那么,种植花草的面积为 ▲
的道路,余下部分种植花草.那么,种植花草的面积为 ▲ ![]() .
.
16.已知![]() ,则
,则![]() ▲ .
▲ .
![]()

17.小明玩一种的游戏,每次挪动珠子的颗数与对应所得的分数如下表:
挪动珠子数(颗) | 2 | 3 | 4 | 5 | 6 | …… |
对应所得分数(分) | 2 | 6 | 12 | 20 | 30 | …… |
当对应所得分数为132分时,则挪动的珠子数为 ▲ 颗.
18.如图,在第一象限内,点P,M![]() 是双曲线
是双曲线![]() 上的两点,PA⊥
上的两点,PA⊥![]() 轴于点A,MB⊥
轴于点A,MB⊥![]() 轴于点B,PA与OM交于点C,则△OAC的面积为 ▲ .
轴于点B,PA与OM交于点C,则△OAC的面积为 ▲ .
三、解答题(本题共9小题,共88分。答题请用0.5毫米黑色墨水签字笔或钢笔书写在答题卡的相应位置上。解答是应写出必要的文字说明,证明过程或演算步骤。)
19.(6分)计算:![]()
20.(8分)解方程:![]()
21.(8分)在一个不透明的盒子里,装有三个分别写有数字-1、0、1的乒乓球(形状、大小一样),先从盒子里随机取出一个乒乓球,记下数字后放回盒子,摇匀后再随机取 出一个乒乓球,记下数字.
(1)请用树状图或列表的方法求两次取出乒乓球上的数字相同的概率;
(2)求两次取出乒乓球上的数字之积等于0的概率.
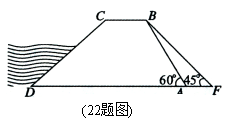
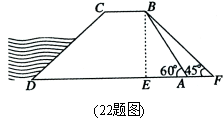
22.(10分)如图,水坝的横断面是梯形,背水坡AB的坡
角∠BAD=![]() ,坡长AB=
,坡长AB=![]() ,为加强水坝强度,
,为加强水坝强度,
将坝底从A处向后水平延伸到F处,使新的背水坡
的坡角∠F=![]() ,求AF的长度(结果精确到1米,
,求AF的长度(结果精确到1米,
参考数据: ![]() ,
,![]() ).
).
23.(10分)某校七年级(1)班为了在王强和李军两同学中选班长,进行了一次“演讲”与“民主测评”活动,A、B、C、D、E五位老师作为评委对王强、李军的“演讲”打分;该班50名同学分别对王强和李军按“好”、“较好”、“一般”三个等级进行民主测评。统计结果如下图、表.计分规则:
①“演讲”得分按“去掉一个最高分和一个最低分后计算平均分”;
②“民主测评”分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;
③综合分=“演讲”得分×40%+“民主测评”得分×60%.
解答下列问题:
(1)演讲得分,王强得 ▲ 分;李军得 ▲ 分;
(2)民主测评得分,王强得 ▲ 分; 李军得 ▲ 分;
(3)以综合得分高的当选班长,王强和李军谁能当班长?为什么?
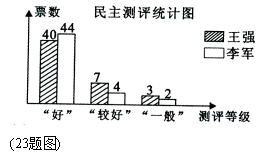
![]() 演讲得分表(单位:分)
演讲得分表(单位:分)
评委 姓名 | A | B | C | D | E |
王强 | 90 | 92 | 94 | 97 | 82 |
李军 | 89 | 82 | 87 | 96 | 91 |
24.(10分)如图(1),在△ABC和△EDC中,AC=CE=CB=CD,∠ACB=∠ECD=![]() ,AB与CE交于F,ED与AB、BC分别交于M、H.
,AB与CE交于F,ED与AB、BC分别交于M、H.
(1)求证:CF=CH;
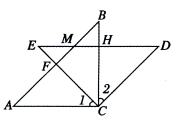
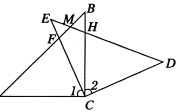 (2)如图(2),△ABC不动,将△EDC绕点C旋转到∠BCE=
(2)如图(2),△ABC不动,将△EDC绕点C旋转到∠BCE=![]() 时,试判断四边形ACDM是什么四边形?并证明你的结论.
时,试判断四边形ACDM是什么四边形?并证明你的结论.
![]()
![]()
25.(10分)某酒厂每天生产A、B两种品牌的白酒共600瓶,A、B两种品牌的白酒每瓶的成本和利润如下表:
| A | B |
成本(元/瓶) | 50 | 35 |
利润(元/瓶) | 20 | 15 |
设每天生产A种品牌的白酒![]() 瓶,每天获利
瓶,每天获利![]() 元.
元.
(1)请写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果该酒厂每天至少投入成本26400元,那么每天至少获利多少元?
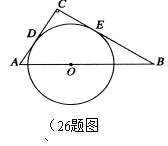
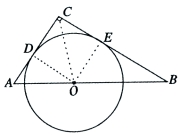
26.(12分)如图,在△ABC中,∠C=![]() ,AC+BC=8,点O是
,AC+BC=8,点O是
斜边AB上一点,以O为圆心的⊙O分别与AC、BC相切于
点D、E.
(1)当AC=2时,求⊙O的半径;
(2)设AC=![]() ,⊙O的半径为
,⊙O的半径为![]() ,求
,求![]() 与
与![]() 的函数关系式.
的函数关系式.
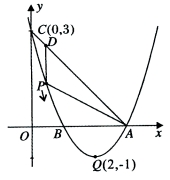
27.(14分)如图,已知抛物线![]() 的顶点坐
的顶点坐
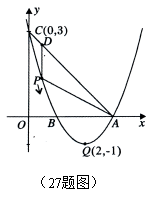 标为Q
标为Q![]() ,且与
,且与![]() 轴交于点C
轴交于点C![]() ,与
,与![]() 轴交于A、B两
轴交于A、B两
点(点A在点B的右侧),点P是该抛物线上一动点,从点C
沿抛物线向点A运动(点P与A不重合),过点P作PD∥![]() 轴,
轴,
交AC于点D.
(1)求该抛物线的函数关系式;
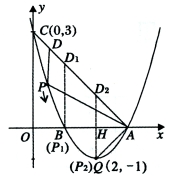
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在问题(2)的结论下,若点E在![]() 轴上,点F在抛物线上,
轴上,点F在抛物线上,
问是否存在以A、P、E、F为顶点的平行四边形?若存在,
求点F的坐标;若不存在,请说明理由.
机密★启用前
2018年遵义中考数学模拟试题参考答案
一、选择题(每小题3分,共30分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | D | B | B | D | B | A | C | C | A | C |
二、填空题(每小题4分,共32分)
11.6.96×![]() 12.
12.![]() 13.50 14.
13.50 14.![]()
15.1131 16.2010 17.12 18.![]()
三、解答题(共9小题,共88分)
19.(6分)解:![]() =
=![]()
=![]()
20.(8分)解:方程两边同乘以![]() ,得:
,得:
![]()
合并:2![]() -5=-3
-5=-3
∴ ![]() =1
=1
经检验,![]() =1是原方程的解.
=1是原方程的解.
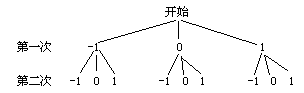 21.(8分)解:(1)树状图为:
21.(8分)解:(1)树状图为:
共9种情况,两次数字相同的有3种.
∴P(两次数字相同)=![]()
(2)(2分)数字之积为0有5种情况,
∴P(两数之积为0) ![]()
22.(10分)解:过B作BE⊥AD于E
在Rt△ABE中,∠BAE=![]() , ∴∠ABE=
, ∴∠ABE=![]()
 ∴AE=
∴AE=![]() AB
AB![]()
∴BE![]()
∴在Rt△BEF中, ∠F=![]() , ∴EF=BE=30
, ∴EF=BE=30
∴AF=EF-AE=30-![]()
∵![]() , ∴AF=12.68
, ∴AF=12.68![]() 13
13
23.(10分)解:
(1)(4分)王强得 92 分;李军得 89 分;
(2)(4分)民主测评王强得 87 分; 李军得 92 分;
(3)(2分)王强综合分=92×40%+87×60%=89分
李军综合分=89×40%+92×60%=90.8分
∵90.8>89, ∴李军当班长.
24.(10分)解:(1)(5分) 证明:在△ACB和△ECD中
 ∵∠ACB=∠ECD=
∵∠ACB=∠ECD=![]()
∴∠1+∠ECB=∠2+∠ECB,
∴∠1=∠2
又∵AC=CE=CB=CD,
∴∠A=∠D=![]()
∴△ACB≌△ECD,
∴CF=CH
(2)(5分) 答: 四边形ACDM是菱形
 证明: ∵∠ACB=∠ECD=
证明: ∵∠ACB=∠ECD=![]() , ∠BCE=
, ∠BCE=![]()
∴∠1=![]() , ∠2=
, ∠2=![]()
又∵∠E=∠B=![]() ,
,
∴∠1=∠E, ∠2=∠B
∴AC∥MD, CD∥AM , ∴ACDM是平行四边形
又∵AC=CD, ∴ACDM是菱形
25.(10分)解:(1)(4分) ![]() =20
=20![]() +15(600-
+15(600-![]() )
)
即![]() =5
=5![]() +9000
+9000
(2)(6分)根据题意得:
50![]() +35(600-
+35(600-![]() )≥26400
)≥26400
∴![]() ≥360
≥360
当![]() =360时,
=360时, ![]() 有最小值,代入
有最小值,代入![]() =5
=5![]() +9000得
+9000得
![]() =5×360+9000=10800
=5×360+9000=10800
∴每天至少获利10800元.
26.(12分)(1)(5分) 解: 连接OD、OE、OC
∵D、E为切点
 ∴OD⊥AC, OE⊥BC, OD=OE
∴OD⊥AC, OE⊥BC, OD=OE
∵![]()
∴![]() AC·BC=
AC·BC=![]() AC·OD+
AC·OD+![]() BC·OE
BC·OE
∵AC+BC=8, AC=2,∴BC=6
∴![]() ×2×6=
×2×6=![]() ×2×OD+
×2×OD+![]() ×6×OE
×6×OE
而OD=OE,
∴OD=![]() ,即⊙O的半径为
,即⊙O的半径为![]()
(2)(7分)解:连接OD、OE、OC
∵D、E为切点
∴OD⊥AC, OE⊥BC, OD=OE=![]()
∵![]()
∴![]() AC·BC=
AC·BC=![]() AC·OD+
AC·OD+![]() BC·OE
BC·OE
∵AC+BC=8, AC=![]() ,∴BC=8-
,∴BC=8-![]()
∴![]()
![]() (8-
(8-![]() )=
)=![]()
![]()
![]() +
+![]() (8-
(8-![]() )
)![]()
化简:![]()
即:![]()
27.(14分)解:(1)(3分)
∵抛物线的顶点为Q(2,-1)
 ∴设
∴设![]()
将C(0,3)代入上式,得
![]()
![]()
∴![]() , 即
, 即![]()
(2)(7分)分两种情况:
①(3分)当点P1为直角顶点时,点P1与点B重合(如图)
令![]() =0, 得
=0, 得![]()
解之得![]() ,
, ![]()
∵点A在点B的右边, ∴B(1,0), A(3,0)
∴P1(1,0)
②(4分)解:当点A为△APD2的直角顶点是(如图)
∵OA=OC, ∠AOC=![]() , ∴∠OAD2=
, ∴∠OAD2=![]()
当∠D2AP2=![]() 时, ∠OAP2=
时, ∠OAP2=![]() , ∴AO平分∠D2AP2
, ∴AO平分∠D2AP2
又∵P2D2∥![]() 轴, ∴P2D2⊥AO, ∴P2、D2关于
轴, ∴P2D2⊥AO, ∴P2、D2关于![]() 轴对称.
轴对称.
设直线AC的函数关系式为![]()
将A(3,0), C(0,3)代入上式得
![]() , ∴
, ∴![]()
∴![]()
∵D2在![]() 上, P2在
上, P2在![]() 上,
上,
∴设D2(![]() ,
,![]() ), P2(
), P2(![]() ,
,![]() )
)
∴(![]() )+(
)+(![]() )=0
)=0
![]() , ∴
, ∴![]() ,
, ![]() (舍)
(舍)
∴当![]() =2时,
=2时, ![]()
=![]() =-1
=-1
∴P2的坐标为P2(2,-1)(即为抛物线顶点)
∴P点坐标为P1(1,0), P2(2,-1)
(3)(4分)解: 由题(2)知,当点P的坐标为P1(1,0)时,不能构成平行四边形
当点P的坐标为P2(2,-1)(即顶点Q)时,
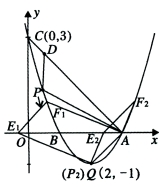 平移直线AP(如图)交
平移直线AP(如图)交![]() 轴于点E,交抛物线于点F.
轴于点E,交抛物线于点F.
当AP=FE时,四边形PAFE是平行四边形
∵P(2,-1), ∴可令F(![]() ,1)
,1)
∴![]()
解之得: ![]() ,
, ![]()
∴F点有两点,即F1(![]() ,1), F2(
,1), F2(![]() ,1)
,1)
1

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...