2017年遵义中考数学试题word版（含答案）

各位同学在查看时请点击全屏查看

2017年遵义中考数学试题

一、数学试题选择题（本大题共12小题，每小题3分，共36分）

1．﹣3的相反数是（　　）

A．﹣3              B．3              C．              D．

2．2017年遵义市固定资产总投资计划为2580亿元，将2580亿元用科学记数法表示为（　　）

A．2.58×1011              B．2.58×1012              C．2.58×1013              D．2.58×1014

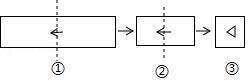
3．把一张长方形纸片按如图①，图②的方式从右向左连续对折两次后得到图③，再在图③中挖去一个如图所示的三角形小孔，则重新展开后得到的图形是（　　）

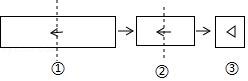
A．              B．              C．              D．

4．下列运算正确的是（　　）

A．2a5﹣3a5=a5              B．a2•a3=a6              C．a7÷a5=a2              D．（a2b）3=a5b3

5．我市连续7天的最高气温为：28°，27°，30°，33°，30°，30°，32°，这组数据的平均数和众数分别是（　　）

A．28°，30°              B．30°，28°              C．31°，30°              D．30°，30°

6．把一块等腰直角三角尺和直尺如图放置，如果∠1=30°，则∠2的度数为（　　）

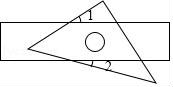
A．45°              B．30°              C．20°              D．15°

7．不等式6﹣4x≥3x﹣8的非负整数解为（　　）

A．2个              B．3个              C．4个              D．5个

8．已知圆锥的底面积为9πcm2，母线长为6cm，则圆锥的侧面积是（　　）

A．18πcm2              B．27πcm2              C．18cm2              D．27cm2

9．关于x的一元二次方程x2+3x+m=0有两个不相等的实数根，则m的取值范围为（　　）

A．m≤              B．m              C．m≤              D．m

10．如图，△ABC的面积是12，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG的面积是（　　）

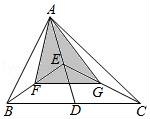
A．4.5              B．5              C．5.5              D．6

11．如图，抛物线y=ax2+bx+c经过点（﹣1，0），对称轴l如图所示，则下列结论：①abc＞0；②a﹣b+c=0；③2a+c＜0；④a+b＜0，其中所有正确的结论是（　　）

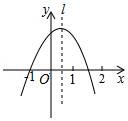
A．①③              B．②③              C．②④              D．②③④

12．如图，△ABC中，E是BC中点，AD是∠BAC的平分线，EF∥AD交AC于F．若AB=11，AC=15，则FC的长为（　　）

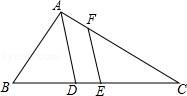
A．11              B．12              C．13              D．14

二、填空题（本大题共6小题，每小题4分，共24分）

13．计算： =　   　．

14．一个正多边形的一个外角为30°，则它的内角和为　   　．

15．按一定规律排列的一列数依次为：，1，，，，，…，按此规律，这列数中的第100个数是　   　．

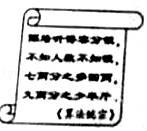
16．明代数学家程大位的《算法统宗》中有这样一个问题（如图），其大意为：有一群人分银子，如果每人分七两，则剩余四两；如果每人分九两，则还差八两，请问：所分的银子共有　   　两．（注：明代时1斤=16两，故有“半斤八两”这个成语）

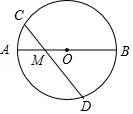
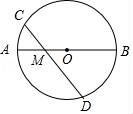
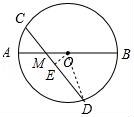
17．如图，AB是⊙O的直径，AB=4，点M是OA的中点，过点M的直线与⊙O交于C，D两点．若∠CMA=45°，则弦CD的长为　   　．

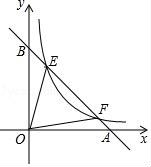
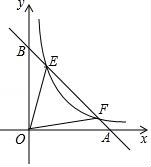
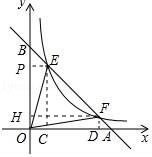
18．如图，点E，F在函数y=的图象上，直线EF分别与x轴、y轴交于点A、B，且BE：BF=1：3，则△EOF的面积是　   　．

三、解答题（本大题共9小题，共90分）

19．计算：|﹣2|+（4﹣π）0﹣+（﹣1）﹣2017．

20．化简分式：（﹣）÷，并从1，2，3，4这四个数中取一个合适的数作为x的值代入求值．

21．学校召集留守儿童过端午节，桌上摆有甲、乙两盘粽子，每盘中盛有白粽2个，豆沙粽1个，肉粽1个（粽子外观完全一样）．

（1）小明从甲盘中任取一个粽子，取到豆沙粽的概率是　   　；

（2）小明在甲盘和乙盘中先后各取了一个粽子，请用树状图或列表法求小明恰好取到两个白粽子的概率．

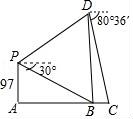
22．乌江快铁大桥是快铁渝黔线的一项重要工程，由主桥AB和引桥BC两部分组成（如图所示），建造前工程师用以下方式做了测量；无人机在A处正上方97m处的P点，测得B处的俯角为30°（当时C处被小山体阻挡无法观测），无人机飞行到B处正上方的D处时能看到C处，此时测得C处俯角为80°36′．

（1）求主桥AB的长度；[来源:学科网]

（2）若两观察点P、D的连线与水平方向的夹角为30°，求引桥BC的长．

（长度均精确到1m，参考数据：≈1.73，sin80°36′≈0.987，cos80°36′≈0.163，tan80°36′≈6.06）

23．贵州省是我国首个大数据综合试验区，大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值，为创建大数据应用示范城市，我市某机构针对市民最关心的四类生活信息进行了民意调查（被调查者每人限选一项），下面是部分四类生活信息关注度统计图表，请根据图中提供的信息解答下列问题：

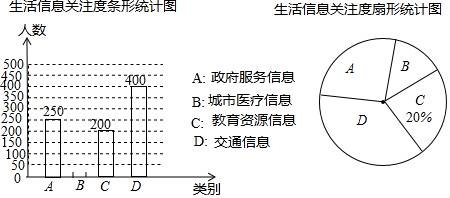
（1）本次参与调查的人数有　   　人；

（2）关注城市医疗信息的有　   　人，并补全条形统计图；

（3）扇形统计图中，D部分的圆心角是　   　度；

（4）说一条你从统计图中获取的信息．

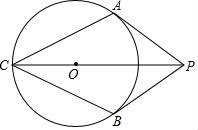
24．如图，PA、PB是⊙O的切线，A、B为切点，∠APB=60°，连接PO并延长与⊙O交于C点，连接AC，BC．

（1）求证：四边形ACBP是菱形；

（2）若⊙O半径为1，求菱形ACBP的面积．

25．为厉行节能减排，倡导绿色出行，今年3月以来．“共享单车”（俗称“小黄车”）公益活动登陆我市中心城区，某公司拟在甲、乙两个街道社区投放一批“小黄车”，这批自行车包括A、B两种不同款型，请回答下列问题：

问题1：单价

该公司早期在甲街区进行了试点投放，共投放A、B两型自行车各50辆，投放成本共计7500元，其中B型车的成本单价比A型车高10元，A、B两型自行车的单价各是多少？

问题2：投放方式

该公司决定采取如下投放方式：甲街区每1000人投放a辆“小黄车”，乙街区每1000人投放辆“小黄车”，按照这种投放方式，甲街区共投放1500辆，乙街区共投放1200辆，如果两个街区共有15万人，试求a的值．

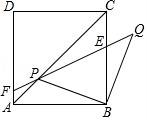
26．边长为2的正方形ABCD中，P是对角线AC上的一个动点（点P与A、C不重合），连接BP，将BP绕点B顺时针旋转90°到BQ，连接QP，QP与BC交于点E，QP延长线与AD（或AD延长线）交于点F．

（1）连接CQ，证明：CQ=AP；

（2）设AP=x，CE=y，试写出y关于x的函数关系式，并求当x为何值时，CE=BC；

（3）猜想PF与EQ的数量关系，并证明你的结论．

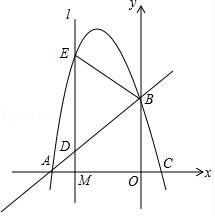
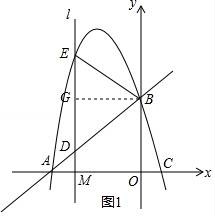
27．如图，抛物线y=ax2+bx﹣a﹣b（a＜0，a、b为常数）与x轴交于A、C两点，与y轴交于B点，直线AB的函数关系式为y=x+．

（1）求该抛物线的函数关系式与C点坐标；

（2）已知点M（m，0）是线段OA上的一个动点，过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点，当m为何值时，△BDE恰好是以DE为底边的等腰三角形？

（3）在（2）问条件下，当△BDE恰好是以DE为底边的等腰三角形时，动点M相应位置记为点M′，将OM′绕原点O顺时针旋转得到ON（旋转角在0°到90°之间）；

i：探究：线段OB上是否存在定点P（P不与O、B重合），无论ON如何旋转，始终保持不变，若存在，试求出P点坐标；若不存在，请说明理由；

ii：试求出此旋转过程中，（NA+NB）的最小值．

2017年遵义中考数学试题参考答案

一、选择题（本大题共12小题，每小题3分，共36分）

1．﹣3的相反数是（　　）

A．﹣3              B．3              C．              D．

【考点】14：相反数．

【分析】依据相反数的定义解答即可．

【解答】解：﹣3的相反数是3．

故选：B．

2．2017年遵义市固定资产总投资计划为2580亿元，将2580亿元用科学记数法表示为（　　）

A．2.58×1011              B．2.58×1012              C．2.58×1013              D．2.58×1014

【考点】1I：科学记数法—表示较大的数．

【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

【解答】解：将2580亿用科学记数法表示为：2.58×1011．

故选：A．

3．把一张长方形纸片按如图①，图②的方式从右向左连续对折两次后得到图③，再在图③中挖去一个如图所示的三角形小孔，则重新展开后得到的图形是（　　）

A．              B．              C．              D．

【考点】P9：剪纸问题．

【分析】解答该类剪纸问题，通过自己动手操作即可得出答案．

【解答】解：重新展开后得到的图形是C，

故选C．

4．下列运算正确的是（　　）

A．2a5﹣3a5=a5              B．a2•a3=a6              C．a7÷a5=a2              D．（a2b）3=a5b3

【考点】48：同底数幂的除法；35：合并同类项；46：同底数幂的乘法；47：幂的乘方与积的乘方．

【分析】根据合并同类项、同底数幂的乘除法以及幂的乘方与积的乘方的计算法则进行解答．

【解答】解：A、原式=﹣a5，故本选项错误；

B、原式=a5，故本选项错误；

C、原式=a2，故本选项正确；

D、原式=a6b3，故本选项错误；

故选：C．

5．我市连续7天的最高气温为：28°，27°，30°，33°，30°，30°，32°，这组数据的平均数和众数分别是（　　）

A．28°，30°              B．30°，28°              C．31°，30°              D．30°，30°

【考点】W5：众数；W1：算术平均数．

【分析】根据平均数和众数的定义及计算公式分别进行解答，即可求出答案．

【解答】解：数据28°，27°，30°，33°，30°，30°，32°的平均数是（28+27+30+33+30+30+32）÷7=30，

30出现了3次，出现的次数最多，则众数是30；

故选D．

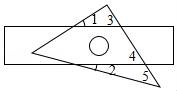
6．把一块等腰直角三角尺和直尺如图放置，如果∠1=30°，则∠2的度数为（　　）

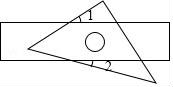[来源:Z+xx+k.Com]

A．45°              B．30°              C．20°              D．15°

【考点】JA：平行线的性质．

【分析】先根据平行线的性质，可得∠4的度数，再根据三角形外角性质，即可得到∠2的度数．

【解答】解：∵∠1=30°，

∴∠3=90°﹣30°=60°，

∵直尺的对边平行，

∴∠4=∠3=60°，

又∵∠4=∠2+∠5，∠5=45°，

∴∠2=60°﹣45°=15°，

故选：D．

7．不等式6﹣4x≥3x﹣8的非负整数解为（　　）

A．2个              B．3个              C．4个              D．5个

【考点】C7：一元一次不等式的整数解．

【分析】首先利用不等式的基本性质解不等式，再从不等式的解集中找出适合条件的非负整数即可．

【解答】解：移项得，﹣4x﹣3x≥﹣8﹣6，

合并同类项得，﹣7x≥﹣14，

系数化为1得，x≤2．

故其非负整数解为：0，1，2，共3个．

故选B．

8．已知圆锥的底面积为9πcm2，母线长为6cm，则圆锥的侧面积是（　　）

A．18πcm2              B．27πcm2              C．18cm2              D．27cm2

【考点】MP：圆锥的计算．

【分析】首先根据圆锥的底面积求得圆锥的底面半径，然后代入公式求得圆锥的侧面积即可．

【解答】解：∵圆锥的底面积为9πcm2，

∴圆锥的底面半径为3，

∵母线长为6cm，

∴侧面积为3×6π=18πcm2，

故选A；

9．关于x的一元二次方程x2+3x+m=0有两个不相等的实数根，则m的取值范围为（　　）

A．m≤              B．m              C．m≤              D．m

【考点】AA：根的判别式．

【分析】利用判别式的意义得到△=32﹣4m＞0，然后解不等式即可．

【解答】解：根据题意得△=32﹣4m＞0，

解得m＜．

故选B．

10．如图，△ABC的面积是12，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG的面积是（　　）

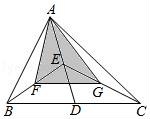
A．4.5              B．5              C．5.5              D．6

【考点】KX：三角形中位线定理；K3：三角形的面积．

【分析】根据中线的性质，可得△AEF的面积=×△ABE的面积=×△ABD的面积=×△ABC的面积=，△AEG的面积=，根据三角形中位线的性质可得△EFG的面积=×△BCE的面积=，进而得到△AFG的面积．

【解答】解：∵点D，E，F，G分别是BC，AD，BE，CE的中点，

∴AD是△ABC的中线，BE是△ABD的中线，CF是△ACD的中线，AF是△ABE的中线，AG是△ACE的中线，

∴△AEF的面积=×△ABE的面积=×△ABD的面积=×△ABC的面积=，

同理可得△AEG的面积=，

△BCE的面积=×△ABC的面积=6，

又∵FG是△BCE的中位线，

∴△EFG的面积=×△BCE的面积=，

∴△AFG的面积是×3=，

故选：A．

11．如图，抛物线y=ax2+bx+c经过点（﹣1，0），对称轴l如图所示，则下列结论：①abc＞0；②a﹣b+c=0；③2a+c＜0；④a+b＜0，其中所有正确的结论是（　　）

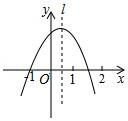
A．①③              B．②③              C．②④              D．②③④

【考点】H4：二次函数图象与系数的关系．

【分析】①根据开口向下得出a＜0，根据对称轴在y轴右侧，得出b＞0，根据图象与y轴的交点在y轴的正半轴上，得出c＞0，从而得出abc＜0，进而判断①错误；

②由抛物线y=ax2+bx+c经过点（﹣1，0），即可判断②正确；

③由图可知，x=2时，y＜0，即4a+2b+c＜0，把b=a+c代入即可判断③正确；

④由图可知，x=2时，y＜0，即4a+2b+c＜0，把c=b﹣a代入即可判断④正确．

【解答】解：①∵二次函数图象的开口向下，

∴a＜0，

∵二次函数图象的对称轴在y轴右侧，

∴﹣＞0，

∴b＞0，

∵二次函数的图象与y轴的交点在y轴的正半轴上，

∴c＞0，

∴abc＜0，故①错误；

②∵抛物线y=ax2+bx+c经过点（﹣1，0），

∴a﹣b+c=0，故②正确；

③∵a﹣b+c=0，∴b=a+c．

由图可知，x=2时，y＜0，即4a+2b+c＜0，

∴4a+2（a+c）+c＜0，

∴6a+3c＜0，∴2a+c＜0，故③正确；

④∵a﹣b+c=0，∴c=b﹣a．

由图可知，x=2时，y＜0，即4a+2b+c＜0，

∴4a+2b+b﹣a＜0，

∴3a+3b＜0，∴a+b＜0，故④正确．

故选D．

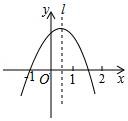
12．如图，△ABC中，E是BC中点，AD是∠BAC的平分线，EF∥AD交AC于F．若AB=11，AC=15，则FC的长为（　　）

A．11              B．12              C．13              D．14

【考点】JA：平行线的性质；KF：角平分线的性质．

【分析】根据角平分线的性质即可得出==，结合E是BC中点，即可得出=，由EF∥AD即可得出==，进而可得出CF=CA=13，此题得解．

【解答】解：∵AD是∠BAC的平分线，AB=11，AC=15，

∴==．

∵E是BC中点，

∴==．

∵EF∥AD，

∴==，

∴CF=CA=13．

故选C．

二、填空题（本大题共6小题，每小题4分，共24分）

13．计算： =　3　．

【考点】78：二次根式的加减法．

【分析】先进行二次根式的化简，然后合并．

【解答】解： =2+

=3．

故答案为：3．

14．一个正多边形的一个外角为30°，则它的内角和为　1800°　．

【考点】L3：多边形内角与外角．

【分析】先利用多边形的外角和等于360度计算出多边形的边数，然后根据多边形的内角和公式计算．

【解答】解：这个正多边形的边数为=12，

所以这个正多边形的内角和为（12﹣2）×180°=1800°．

故答案为1800°．

15．按一定规律排列的一列数依次为：，1，，，，，…，按此规律，这列数中的第100个数是　　．

【考点】37：规律型：数字的变化类．

【分析】根据按一定规律排列的一列数依次为：，，，，，，…，可得第n个数为，据此可得第100个数．

【解答】解：按一定规律排列的一列数依次为：，，，，，，…，

按此规律，第n个数为，

∴当n=100时， =，

即这列数中的第100个数是，

故答案为：．

16．明代数学家程大位的《算法统宗》中有这样一个问题（如图），其大意为：有一群人分银子，如果每人分七两，则剩余四两；如果每人分九两，则还差八两，请问：所分的银子共有　46　两．（注：明代时1斤=16两，故有“半斤八两”这个成语）

【考点】8A：一元一次方程的应用．

【分析】可设有x人，根据有一群人分银子，如果每人分七两，则剩余四两；如果每人分九两，则还差八两，根据所分的银子的总两数相等可列出方程，求解即可．

【解答】解：设有x人，依题意有

7x+4=9x﹣8，

解得x=6，

7x+4=42+4=46．

答：所分的银子共有46两．

故答案为：46．

17．如图，AB是⊙O的直径，AB=4，点M是OA的中点，过点M的直线与⊙O交于C，D两点．若∠CMA=45°，则弦CD的长为　　．

【考点】M2：垂径定理；KQ：勾股定理；KW：等腰直角三角形．

【分析】连接OD，作OE⊥CD于E，由垂径定理得出CE=DE，证明△OEM是等腰直角三角形，由勾股定理得出OE=OM=，在Rt△ODE中，由勾股定理求出DE=，得出CD=2DE=即可．

【解答】解：连接OD，作OE⊥CD于E，如图所示：

则CE=DE，

∵AB是⊙O的直径，AB=4，点M是OA的中点，

∴OD=OA=2，OM=1，

∵∠OME=∠CMA=45°，

∴△OEM是等腰直角三角形，

∴OE=OM=，

在Rt△ODE中，由勾股定理得：DE==，

∴CD=2DE=；

故答案为：．

18．如图，点E，F在函数y=的图象上，直线EF分别与x轴、y轴交于点A、B，且BE：BF=1：3，则△EOF的面积是　　．

【考点】G5：反比例函数系数k的几何意义．

【分析】证明△BPE∽△BHF，利用相似比可得HF=4PE，根据反比例函数图象上点的坐标特征，设E点坐标为（t，），则F点的坐标为（3t，），由于S△OEF+S△OFD=S△OEC+S梯形ECDF，S△OFD=S△OEC=1，所以S△OEF=S梯形ECDF，然后根据梯形面积公式计算即可．

【解答】解：作EP⊥y轴于P，EC⊥x轴于C，FD⊥x轴于D，FH⊥y轴于H，如图所示：

∵EP⊥y轴，FH⊥y轴，

∴EP∥FH，

∴△BPE∽△BHF，

∴=，即HF=3PE，

设E点坐标为（t，），则F点的坐标为（3t，），

∵S△OEF+S△OFD=S△OEC+S梯形ECDF，

而S△OFD=S△OEC=×2=1，

∴S△OEF=S梯形ECDF=（+）（3t﹣t）=；

故答案为：．

三、解答题（本大题共9小题，共90分）

19．计算：|﹣2|+（4﹣π）0﹣+（﹣1）﹣2017．

【考点】2C：实数的运算；6E：零指数幂；6F：负整数指数幂．

【分析】首先计算乘方、开方，然后从左向右依次计算，求出算式的值是多少即可．

【解答】解：|﹣2|+（4﹣π）0﹣+（﹣1）﹣2017

=2+1﹣2﹣1

=0

20．化简分式：（﹣）÷，并从1，2，3，4这四个数中取一个合适的数作为x的值代入求值．

【考点】6D：分式的化简求值．

【分析】利用分式的运算，先对分式化简单，再选择使分式有意义的数代入求值即可．

【解答】解：

（﹣）÷

=[﹣）÷

=（﹣）÷

=×

=x+2，

∵x2﹣4≠0，x﹣3≠0，

∴x≠2且x≠﹣2且x≠3，

∴可取x=1代入，原式=3．

21．学校召集留守儿童过端午节，桌上摆有甲、乙两盘粽子，每盘中盛有白粽2个，豆沙粽1个，肉粽1个（粽子外观完全一样）．

（1）小明从甲盘中任取一个粽子，取到豆沙粽的概率是　　；

（2）小明在甲盘和乙盘中先后各取了一个粽子，请用树状图或列表法求小明恰好取到两个白粽子的概率．

【考点】X6：列表法与树状图法；X4：概率公式．

【分析】（1）由甲盘中一共有4个粽子，其中豆沙粽子只有1个，根据概率公式求解可得；

（2）根据题意画出树状图，由树状图得出一共有16种等可能结果，其中恰好取到两个白粽子有4种结果，根据概率公式求解可得．

【解答】解：（1）∵甲盘中一共有4个粽子，其中豆沙粽子只有1个，

∴小明从甲盘中任取一个粽子，取到豆沙粽的概率是，

故答案为：；

（2）画树状图如下：

由树状图可知，一共有16种等可能结果，其中恰好取到两个白粽子有4种结果，

∴小明恰好取到两个白粽子的概率为=．

22．乌江快铁大桥是快铁渝黔线的一项重要工程，由主桥AB和引桥BC两部分组成（如图所示），建造前工程师用以下方式做了测量；无人机在A处正上方97m处的P点，测得B处的俯角为30°（当时C处被小山体阻挡无法观测），无人机飞行到B处正上方的D处时能看到C处，此时测得C处俯角为80°36′．

（1）求主桥AB的长度；

（2）若两观察点P、D的连线与水平方向的夹角为30°，求引桥BC的长．

（长度均精确到1m，参考数据：≈1.73，sin80°36′≈0.987，cos80°36′≈0.163，tan80°36′≈6.06）

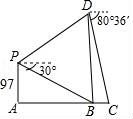
【考点】TA：解直角三角形的应用﹣仰角俯角问题．

【分析】（1）在Rt△ABP中，由AB=可得答案；

（2）由∠ABP=30°、AP=97知PB=2PA=194，再证△PBD是等边三角形得DB=PB=194m，根据BC=可得答案．

【解答】解：（1）由题意知∠ABP=30°、AP=97，

∴AB====97≈168m，

答：主桥AB的长度约为168m；

（2）∵∠ABP=30°、AP=97，

∴PB=2PA=194，

又∵∠DBC=∠DBA=90°、∠PBA=30°，

∴∠DBP=∠DPB=60°，

∴△PBD是等边三角形，

∴DB=PB=194，

在Rt△BCD中，∵∠C=80°36′，

∴BC==≈32，

答：引桥BC的长约为32m.

23．贵州省是我国首个大数据综合试验区，大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值，为创建大数据应用示范城市，我市某机构针对市民最关心的四类生活信息进行了民意调查（被调查者每人限选一项），下面是部分四类生活信息关注度统计图表，请根据图中提供的信息解答下列问题：

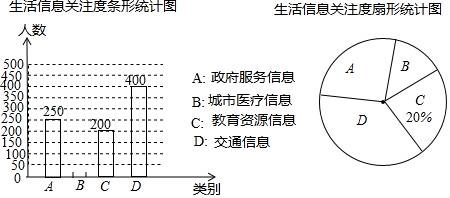
（1）本次参与调查的人数有　1000　人；

（2）关注城市医疗信息的有　150　人，并补全条形统计图；

（3）扇形统计图中，D部分的圆心角是　144　度；

（4）说一条你从统计图中获取的信息．

【考点】VC：条形统计图；VB：扇形统计图．

【分析】（1）由C类别人数占总人数的20%即可得出答案；

（2）根据各类别人数之和等于总人数可得B类别的人数；

（3）用360°乘以D类别人数占总人数的比例可得答案；

（4）根据条形图或扇形图得出合理信息即可．

【解答】解：（1）本次参与调查的人数有200÷20%=1000（人），

故答案为：1000；

（2）关注城市医疗信息的有1000﹣=150人，补全条形统计图如下：

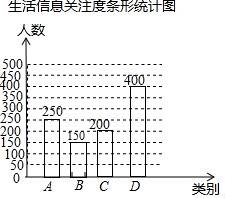
故答案为：150；

（3）扇形统计图中，D部分的圆心角是360°×=144°，

故答案为：144；

（4）由条形统计图可知，市民关注交通信息的人数最多．

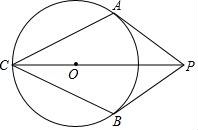
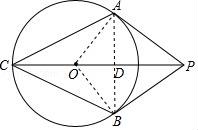
24．如图，PA、PB是⊙O的切线，A、B为切点，∠APB=60°，连接PO并延长与⊙O交于C点，连接AC，BC．

（1）求证：四边形ACBP是菱形；

（2）若⊙O半径为1，求菱形ACBP的面积．

【考点】MC：切线的性质；LA：菱形的判定与性质．

【分析】（1）连接AO，BO，根据PA、PB是⊙O的切线，得到∠OAP=∠OBP=90°，PA=PB，∠APO=∠BPO=∠APB=30°，由三角形的内角和得到∠AOP=60°，根据三角形外角的性质得到∠ACO=30°，得到AC=AP，同理BC=PB，于是得到结论；

（2）连接AB交PC于D，根据菱形的性质得到AD⊥PC，解直角三角形即可得到结论．

【解答】解：（1）连接AO，BO，

∵PA、PB是⊙O的切线，

∴∠OAP=∠OBP=90°，PA=PB，∠APO=∠BPO=∠APB=30°，

∴∠AOP=60°，

∵OA=OC，

∴∠OAC=∠OCA，

∴∠AOP=∠CAO+∠ACO，

∴∠ACO=30°，

∴∠ACO=∠APO，

∴AC=AP，

同理BC=PB，

∴AC=BC=BP=AP，

∴四边形ACBP是菱形；

（2）连接AB交PC于D，

∴AD⊥PC，

∴OA=1，∠AOP=60°，

∴AD=OA=，

∴PD=，

∴PC=3，AB=，

∴菱形ACBP的面积=AB•PC=．

25．为厉行节能减排，倡导绿色出行，今年3月以来．“共享单车”（俗称“小黄车”）公益活动登陆我市中心城区，某公司拟在甲、乙两个街道社区投放一批“小黄车”，这批自行车包括A、B两种不同款型，请回答下列问题：

问题1：单价

该公司早期在甲街区进行了试点投放，共投放A、B两型自行车各50辆，投放成本共计7500元，其中B型车的成本单价比A型车高10元，A、B两型自行车的单价各是多少？

问题2：投放方式

该公司决定采取如下投放方式：甲街区每1000人投放a辆“小黄车”，乙街区每1000人投放辆“小黄车”，按照这种投放方式，甲街区共投放1500辆，乙街区共投放1200辆，如果两个街区共有15万人，试求a的值．

【考点】B7：分式方程的应用；9A：二元一次方程组的应用．

【分析】问题1：设A型车的成本单价为x元，则B型车的成本单价为（x+10）元，根据成本共计7500元，列方程求解即可；

问题2：根据两个街区共有15万人，列出分式方程进行求解并检验即可．

【解答】解：问题1

设A型车的成本单价为x元，则B型车的成本单价为（x+10）元，依题意得

50x+50（x+10）=7500，

解得x=70，

∴x+10=80，

答：A、B两型自行车的单价分别是70元和80元；

问题2

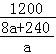由题可得，×1000+×1000=150000，

解得a=15，

经检验：a=15是所列方程的解，

故a的值为15．

26．边长为2的正方形ABCD中，P是对角线AC上的一个动点（点P与A、C不重合），连接BP，将BP绕点B顺时针旋转90°到BQ，连接QP，QP与BC交于点E，QP延长线与AD（或AD延长线）交于点F．

（1）连接CQ，证明：CQ=AP；[来源:.Com]

（2）设AP=x，CE=y，试写出y关于x的函数关系式，并求当x为何值时，CE=BC；

（3）猜想PF与EQ的数量关系，并证明你的结论．

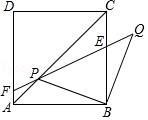
【考点】LO：四边形综合题．

【分析】（1）证出∠ABP=∠CBQ，由SAS证明△BAP≌△BCQ可得结论；

（2）如图1证明△APB∽△CEP，列比例式可得y与x的关系式，根据CE=BC计算CE的长，即y的长，代入关系式解方程可得x的值；

（3）如图3，作辅助线，构建全等三角形，证明△PGB≌△QEB，得EQ=PG，由F、A、G、P四点共圆，

得∠FGP=∠FAP=45°，所以△FPG是等腰直角三角形，可得结论．[来源:学科网]

如图4，当F在AD的延长线上时，同理可得结论．

【解答】（1）证明：如图1，∵线段BP绕点B顺时针旋转90°得到线段BQ，

∴BP=BQ，∠PBQ=90°．

∵四边形ABCD是正方形，

∴BA=BC，∠ABC=90°．

∴∠ABC=∠PBQ．

∴∠ABC﹣∠PBC=∠PBQ﹣∠PBC，即∠ABP=∠CBQ．

在△BAP和△BCQ中，

∵，

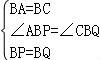∴△BAP≌△BCQ（SAS）．

∴CQ=AP；

（2）解：如图1，∵四边形ABCD是正方形，

∴∠BAC=∠BAD=45°，∠BCA=∠BCD=45°，

∴∠APB+∠ABP=180°﹣45°=135°，

∵DC=AD=2，

由勾股定理得：AC==4，

∵AP=x，

∴PC=4﹣x，

∵△PBQ是等腰直角三角形，

∴∠BPQ=45°，

∴∠APB+∠CPQ=180°﹣45°=135°，

∴∠CPQ=∠ABP，

∵∠BAC=∠ACB=45°，

∴△APB∽△CEP，

∴，

∴，

∴y=x（4﹣x）=﹣x（0＜x＜4），

由CE=BC==，

∴y=﹣x=，

x2﹣4x=3=0，

（x﹣3）（x﹣1）=0，

x=3或1，

∴当x=3或1时，CE=BC；

（3）解：结论：PF=EQ，理由是：

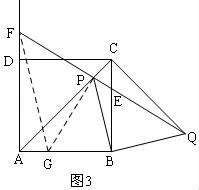
如图3，当F在边AD上时，过P作PG⊥FQ，交AB于G，则∠GPF=90°，

∵∠BPQ=45°，

∴∠GPB=45°，

∴∠GPB=∠PQB=45°，

∵PB=BQ，∠ABP=∠CBQ，

∴△PGB≌△QEB，

∴EQ=PG，

∵∠BAD=90°，

∴F、A、G、P四点共圆，

连接FG，

∴∠FGP=∠FAP=45°，

∴△FPG是等腰直角三角形，

∴PF=PG，

∴PF=EQ．

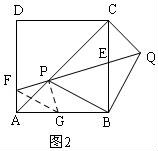
当F在AD的延长线上时，如图4，同理可得：PF=PG=EQ．

27．如图，抛物线y=ax2+bx﹣a﹣b（a＜0，a、b为常数）与x轴交于A、C两点，与y轴交于B点，直线AB的函数关系式为y=x+．

（1）求该抛物线的函数关系式与C点坐标；

（2）已知点M（m，0）是线段OA上的一个动点，过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点，当m为何值时，△BDE恰好是以DE为底边的等腰三角形？

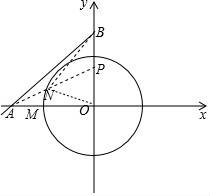
（3）在（2）问条件下，当△BDE恰好是以DE为底边的等腰三角形时，动点M相应位置记为点M′，将OM′绕原点O顺时针旋转得到ON（旋转角在0°到90°之间）；

i：探究：线段OB上是否存在定点P（P不与O、B重合），无论ON如何旋转，始终保持不变，若存在，试求出P点坐标；若不存在，请说明理由；

ii：试求出此旋转过程中，（NA+NB）的最小值．

【考点】HF：二次函数综合题．

【分析】（1）根据已知条件得到B（0，），A（﹣6，0），解方程组得到抛物线的函数关系式为：y=﹣x2﹣x+，于是得到C（1，0）；

（2）由点M（m，0），过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点，得到D（m， m+），当DE为底时，作BG⊥DE于G，根据等腰三角形的性质得到EG=GD=ED，GM=OB=，列方程即可得到结论；

（3）i：根据已知条件得到ON=OM′=4，OB=，由∠NOP=∠BON，特殊的当△NOP∽△BON时，根据相似三角形的性质得到=，于是得到结论；

ii：根据题意得到N在以O为圆心，4为半径的半圆上，由（i）知， =，得到NP=NB，于是得到（NA+NB）的最小值=NA+NP，此时N，A，P三点共线，根据勾股定理得到结论．

【解答】解：（1）在y=x+中，令x=0，则y=，令y=0，则x=﹣6，

∴B（0，），A（﹣6，0），

把B（0，），A（﹣6，0）代入y=ax2+bx﹣a﹣b得，

∴，

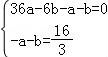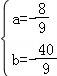∴抛物线的函数关系式为：y=﹣x2﹣x+，

令y=0，则=﹣x2﹣x+=0，

∴x1=﹣6，x2=1，

∴C（1，0）；

（2）∵点M（m，0），过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点，

∴D（m， m+），当DE为底时，

作BG⊥DE于G，则EG=GD=ED，GM=OB=，

∴m+（﹣m2﹣m++m+）=，

解得：m1=﹣4，m2=9（不合题意，舍去），[来源:Z§xx§k.Com]

∴当m=﹣4时，△BDE恰好是以DE为底边的等腰三角形；

（3）i：存在，

∵ON=OM′=4，OB=，

∵∠NOP=∠BON，

∴当△NOP∽△BON时， =，

∴不变，

即OP==3，

∴P（0，3）

ii：∵N在以O为圆心，4为半径的半圆上，由（i）知， =，

∴NP=NB，

∴（NA+NB）的最小值=NA+NP，

∴此时N，A，P三点共线，

∴（NA+NB）的最小值==3．