各位同学在查看时请点击全屏查看
2018年昆明中考数学模拟试题
(全卷共三个大题,共23个小题,共4页;满分120分,考试时间120分钟)
一、数学模拟试题填空题(本大题共6小题,每小题3分,共18分)
1.-的相反数为____.
2.今年1至4月份,我省旅游业一直保持良好的发展势头,旅游收入累计达5 163 000 000元,用科学记数法表示是__5.163×109__元.
3.二次根式有意义的取值范围是__x≥5__.
4.如图,用一个圆心角为90°,半径为4的扇形围成一个圆锥的侧面,该圆锥底面圆的半径为__1__.
5.如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为__70°__.
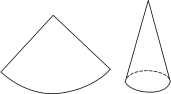 (第4题图)
(第4题图)
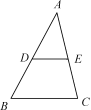 (第5题图)
(第5题图)
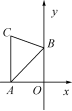 (第6题图)
(第6题图)
6.如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=2,点D为AC与反比例函数y=的图象的交点,若直线BD将△ABC的面积分成1∶2的两部分,则k的值为__-4或-8__.
二、选择题(本大题共8小题,每小题只有一个正确答案,每小题4分,共32分)
7.-6的绝对值是( B )
A.-6 B.6 C.±6 D.-
8.下列运算正确的是( D )
A.5x-3x=2 B.(x-1)2=x2-1
C.(-2x2)3=-6x6 D.x6÷x2=x4
9.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表:
跳高成绩(m) | 1.50 | 1.55 | 1.60 | 1.65 | 1.70 | 1.75 |
跳高人数 | 1 | 3 | 2 | 3 | 5 | 1 |
这些运动员跳高成绩的中位数和众数分别是( A )
A.1.65,1.70 B.1.70,1.65 C.1.70,1.70 D.3,5
10.如图,在长为100 m,宽为80 m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7 644 m2,则道路的宽应为多少米?设道路的宽为x m,则可列方程为( C )
A.100×80-100x-80x=7 644 B.(100-x)(80-x)+x2=7 644
C.(100-x)(80-x)=7 644 D.100x+80x=356
 (第10题图)
(第10题图)
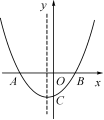 (第11题图)
(第11题图)
11.如图,抛物线y=ax2+bx+c的图象交x轴于A(-2,0)和点B,交y轴负半轴于点C,且OB=OC.下列结论:
①2a-c=2;②a=;③ac=b-1;④>0.
其中正确的个数有( C )
A.1个 B.2个 C.3个 D.4个
12.已知关于x的一元二次方程mx2-(m+2)x+2=0有两个不相等的实数根x1,x2.则m的取值范围是( A )
A.m≠0且m≠2 B.m≠0
C.m≠2 D.m≠-2
13.如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠CDB=,BD=5,则OH的长度为( D )
A. B. C.1 D.
 (第13题图)
(第13题图)
 (第14题图)
(第14题图)
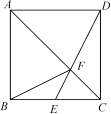
14.如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是( C )
A.①③ B.②③ C.①④ D.②④
三、解答题(本大题共9小题,共70分)
15.(6分)先化简÷,再求值,请你从-1≤x<3的范围内选取一个你喜欢的整数作为x的值.
解:原式=÷
=·
=,
由-1≤x<3,x为整数,得到x=-1,0,1,2,
经检验,x=-1,0,1不合题意,舍去,
则当x=2时,原式=4.
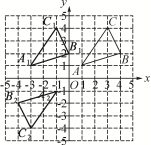
16.(7分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
解:(1)如图所示;
(2)如图所示;
(3)点P的坐标为(2,0).
17.(7分)如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.
求证:△ADF≌△BCE.

证明:∵AE=BF,
∴AE+EF=BF+EF,即AF=BE.
在△ADF和△BCE中,
∴△ADF≌△BCE.
18.(7分)某校为了解九年级学生近两个月“推荐书目”的阅读情况,随机抽取了该年级的部分学生,
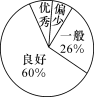
调查了他们每人“推荐书目”的阅读本数.设每名学生的阅读本数为n,并按以下规定分为四档:当n<3时,为“偏少”;当3≤n<5时,为“一般”;当5≤n<8时,为“良好”;当n≥8时,为“优秀”.将调查结果统计后绘制成如图不完整的统计图表:
阅读本数n(本) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数(名) | 1 | 2 | 6 | 7 | 12 | x | 7 | y | 1 |
请根据以上信息回答下列问题:
(1)分别求出统计表中的x,y的值;
(2)估计该校九年级400名学生中为“优秀”档次的人数;
(3)从被调查的“优秀”档次的学生中随机抽取2名学生介绍读书体会,请用列表或画树状图的方法求抽取的2名学生中有1名阅读本数为9的概率.
解:(1)由图表可知被调查学生中“一般”档次的有6+7=13(人),所占的比例是26%,所以调查的学生总数是13÷26%=50.
则调查学生中“良好”档次的人数为50×60%=30,
所以x=30-(12+7)=11,
y=50-(1+2+6+7+12+11+7+1)=3;
(2)由样本数据可知“优秀”档次所占的比例是=0.08=8%,
400×8%=32(人),
∴估计九年级400名学生中为“优秀”档次的人数为32人;
(3)分别用A,B,C表示阅读本数是8的学生,用D表示阅读本数是9的学生,根据题意画出树状图:
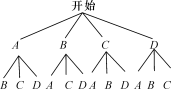
或列表:
| A | B | C | D |
A |
| (A,B) | (A,C) | (A,D) |
B | (B,A) |
| (B,C) | (B,D) |
C | (C,A) | (C,B) |
| (C,D) |
D | (D,A) | (D,B) | (D,C) |
|
由树状图或列表可知,共有12种等可能的结果,其中所抽取的2名学生中有1名阅读本数为9的有6种.
∴抽取的2名学生中有1名阅读本数为9的概率P==.
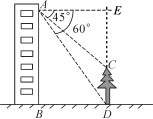
19.(7分)如图,小明在自家楼房的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为45°,树底D处的俯角为60°,楼底到大树的距离BD为20 m.请你帮助小明计算树的高度.(精确到0.1 m)
解:过点A作AE∥BD交DC的延长线于点E.
则∠AEC=∠BDC=90°.
∵∠EAC=45°,∴∠ECA=45°,∴AE=CE.
∵AE=BD=20,
∴EC=20.
∵tan∠EAD=,
∴ED=20·tan60°=20,
CD=ED-EC=20-20≈14.6(m).
答:树高约为14.6 m.
20.(7分)“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车去年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元;(用列方程的方法解答)
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如表:
| A型车 | B型车 |
进货价格(元/辆) | 1 100 | 1 400 |
销售价格(元/辆) | 今年的销售价格 | 2 400 |
解:(1)设去年A型车每辆x元,那么今年每辆(x+400)元.
根据题意得=,
解得x=1 600,
经检验,x=1 600是方程的解.∴x+400=2 000.
答:今年A型车每辆2 000元;
(2)设今年7月份进A型车m辆,则B型车(50-m)辆,获得的总利润为y元.
根据题意得50-m≤2m,解得m≥16,m为整数.
y=(2 000-1 100)m+(2 400-1 400)(50-m)
=-100m+50 000,
∵-100<0,∴y随m的增大而减小,
∴当m=17时,可以获得最大利润.
答:进货方案是A型车17辆,B型车33辆.
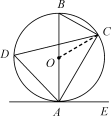
21.(8分)如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
解:(1)∵∠ABC与∠D都是所对的圆周角,
∴∠ABC=∠D=60°;
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=90°-60°=30°,
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,
即BA⊥AE,∴AE是⊙O的切线;
(3)连接OC.
∵∠ABC=60°,∴∠AOC=120°,
∴OB=OC=BC=4,
∴劣弧AC的长为=π.
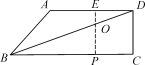
22.(9分)已知:如图,在四边形ABCD中,AD∥BC,∠DCB=90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.
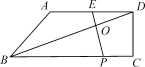
(1)当P点在BC边上运动时,求证:△BOP∽△DOE;
(2)设(1)中的相似比为k,若AD∶BC=2∶3.请探究:当k为下列三种情况时,四边形ABPE是什么四边形?①当k=1时,是____;②当k=2时,是____;③当k=3时,是____.并证明k=2时的结论.
解:(1)∵AD∥BC,
∴∠OBP=∠ODE.
在△BOP和△DOE中,
∠OBP=∠ODE,
∠BOP=∠DOE,
∴△BOP∽△DOE(有两个角对应相等的两三角形相似)
(2)①平行四边形;
②直角梯形;
③等腰梯形;
证明:∵k=2时,=2,
∴BP=2DE=AD.
∵AD∶BC=2∶3,∴BC=AD,
∴PC=BC-BP=AD-AD=AD=ED,
又∵ED∥PC,∴四边形PCDE是平行四边形.
∵∠DCB=90°,∴四边形PCDE是矩形,
∴∠EPB=90°,
又∵AD∥BC,AB与DC不平行,
∴AE∥BP,AB与EP不平行,
∴四边形ABPE是直角梯形.
23.(12分)如图,已知抛物线y=ax2+bx-3(a≠0)与x轴交于A,B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,-3).
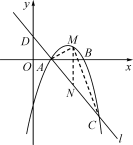
(1)求抛物线的解析式;
(2)点M是(1)中抛物线上一个动点,且位于直线AC的上方,试求△ACM的最大面积以及此时点M的坐标;
(3)抛物线上是否存在点P,使得△PAC是以AC为直角边的直角三角形?如果存在,求出P点的坐标;如果不存在,请说明理由.
解:(1)将A(1,0),C(4,-3)代入y=ax2+bx-3得
解得
即抛物线的解析式为:y=-x2+4x-3;
(2)设M(a,-a2+4a-3),
设直线AC的解析式为y=kx+b,将A(1,0),C(4,-3)代入得
解得
∴直线AC的解析式为:y=1-x.
如图,过M作x轴的垂线交AC于点N,则N(a,1-a),
则MN=yM-yN=-a2+4a-3-(1-a)=-a2+5a-4.
S△AMC=S△AMN+S△CMN
=·MN·(xC-xA)
=(3-1)(-a2+5a-4)
=-+,
当a=时,面积最大,且为,
此时M;
(3)存在,理由如下:
当∠ACP=90°时,由AC斜率为-1,可得CP斜率为1,
此时CP:y=x-7,
由CP解析式和抛物线解析式得:
解得:或(不合题意,舍去),
∴P(-1,-8);
当∠CAP=90°时,由AC的斜率为-1,可得AP的斜率为1,
此时AP:y=x-1,
由AP解析式和抛物线解析式得:
解得:或(不合题意,舍去),
∴P(2,1).
故存在点P,且为(-1,-8)或(2,1),使得△PAC是以AC为直角边的直角三角形.
第1页

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...