2017天门市中考数学试题【精编版无答案】

请点击全屏查看

2017天门市中考数学试题

本试题卷共6页，满分120分，考试时间120分钟

一、选择题（本大题共有10个小题，每小题3分，满分30分.） 

在下列各小题中，均给出四个答案，其中有且只有一个正确答案，请将正确答案的字母代号在答题卡上涂黑，涂错或不涂均为零分.

1．实数0是

   A．有理数           B．无理数           C．正数                         D．负数

2．一列高速动车组进行了“300 000公里正线运营考核”，标志着中国高铁车从“中国制造”到“中国创新”的飞跃．将数300 000用科学记数法表示为

   A．                                                        B．                                          C．                                          D．

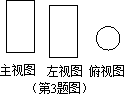
3．如图是一个几何体的三视图，则该几何体的展开图可以是

4．质检部门为了检测某品牌电器的质量，从同一批次共10 000件产品中随机抽取100件进行检测，检测出次品5件.由此估计这一批次产品中的次品件数是

A．5                                                                      B．100                                                        ]C．500                                                        D．10000

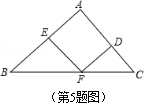5（2017天门数学）．如图，在△ABC中，点D、E、F分别是三条边上的点，EF∥AC，DF∥AB，∠B=45°，∠C=60°．则∠EFD等于

A．80°                   B．75°                   C．70°                                D．65°

6．已知是二元一次方程组的解，则的

算术平方根为

A．4                                          B．2                                          C．                                          D． ±2

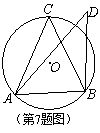
7．如图，锐角△ABC内接于⊙O，点D在⊙O外（与点C在AB同侧），

  ∠ABD=90°，下列结论： ①；②；

③，正确的结论为

    A．①②     B．②③     C．①②③     D．①③

8．（2017天门数学）平面直角坐标系中，过点（-2，3）的直线经过一、二、三象限，若点（0，），

（-1，），（，-1）都在直线上，则下列判断正确的是

A.                                 B.                                              C.                     D.

9．如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下面四个结论：①OA=OD；②AD⊥EF；③当∠BAC=90°时，

四边形AEDF是正方形；④AE2+DF2=AF2+DE2．

其中正确的是

A.②③                                   B. ②④    

C. ②③④                                  D. ①③④

10．如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆 O1，O2，O3，…

组成一条平滑的曲线，点P从原点O出发，

沿这条曲线向右运动，速度为每秒个单

位长度，则第2017秒时，点P的坐标是

    A.（2016，0）                  B.（2017，-1）

  C.（2017，1）                  D.（2017，0）

二、（2017天门数学）请将结果直接写在横线上.（本大题共6个小题，每小题3分，共18分）

11．将分解因式的结果是　     　　．

12．某校学生会提倡双休日到养老院参加服务活动，首次活动需要7位同学参加，现有包括小杰在内的50位同学报名，因此学生会将从这50位同学中随机抽取7位，小杰被抽到参加首次活动的概率是                 .

13．一个圆锥的底面半径为1 cm，母线长为2 cm，则该圆锥的侧

面积是　　     　　（结果保留π）．

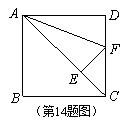
14．如图，已知E是正方形ABCD对角线AC上的一点，AE＝AD，

过点E 作AC的垂线，交边CD于点F，∠FAD＝________度．

15．如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为30°，

测得底部C的俯角为60°，此时航拍无人机与该建筑物的水平

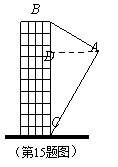距离AD为90米，那么该建筑物的高度BC约为　　　 　米．

（精确到1米，参考数据：≈1.73）

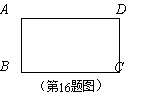
16．如图，矩形ABCD中，BC=2，将矩形ABCD绕点D顺时针旋转

90°，点A、C分别落在点A′、C′处．如果点A′、C′、B

在同一条直线上，那么tan∠ABA′的值为　　　　　　．

三、解答题（本大题共9个小题，满分72分）

17．（2017天门数学）（本题满分5分）

计算：.

18．（本题满分6分）

已知：关于的方程.

（1）不解方程判断该方程根的情况；

（2）若方程有一个根为3，求的值.

19．（本题满分6分）

如图，在△ABC中，点D，E，F分别是AB，BC，CA的

中点，AH是边BC上的高．

（1）求证：四边形ADEF是平行四边形；

（2）求证：∠DHF=∠DEF．

20．（2017天门数学）（本题满分7分）

某校为了了解学生家长对孩子使用手机的态度情况，随机抽取部分学生家长进行问卷调查，发出问卷140份，每位学生的家长1份，每份问卷仅表明一种态度．将回收的问卷进行整理(假设回收的问卷都有效)，并绘制了如下两幅不完整的统计图．

学生家长对孩子使用手机的态度情况统计图

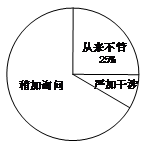
根据以上信息回答下列问题：

（1）回收问卷共      份，“严加干涉”部分对应扇形的圆心角度数为     ；

（2）把条形统计图补充完整；

（3）若将“稍加询问”和“从来不管”视为“管理不严”，已知全校共1500名学生，请估计该校对孩子使用手机“管理不严”的家长大约有多少人？

21．（2017天门数学）（本题满分8分）

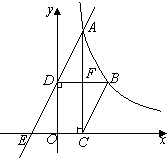如图，已知函数（x＞0）的图象经过点A、B，点B的

坐标为（2，2）．过点A作AC⊥x轴，垂足为C，过点B作

BD⊥y轴，垂足为D，AC与BD交于点F．一次函数y=ax+b

的图象经过点A、D，与x轴的负半轴交于点E．

（1）若AC=OD，求a、b的值；

（2）若BC∥AE，求BC的长．

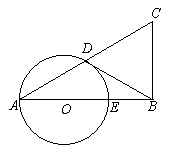22．（本题满分8分）

已知在△ABC中，∠ABC=90o，以AB上的一点O为

圆心，以OA为半径的圆交AC于点D，交AB于点E．

（1）求证：AC·AD=AB·AE；

（2）若BD是⊙O的切线，D是切点，E是OB的

中点，当BC=2时，求AC的长．

23．（本题满分10分）

某游泳馆普通票价20元/张，暑假为了促销，新推出两种优惠卡：

    ① 金卡售价600元/张，每次凭卡不再收费；

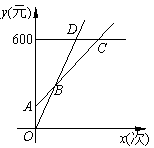② 银卡售价150元/张，每次凭卡另收10元.暑期普通票

正常出售，两种优惠卡仅限暑期使用，不限次数. 设

游泳x次时，所需总费用y元.

（1）分别写出选择银卡、普通票消费时，y与x之间的函

数关系式；

（2）在同一个坐标系中，若三种消费方式对应的函数图象如图所示，请求出点A、B、C的坐标；

（3）请根据函数图象，直接写出选择哪种消费方式更合算．

24．（2017天门数学）（本题满分10分）

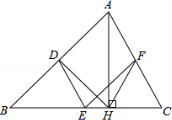
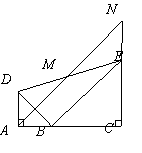
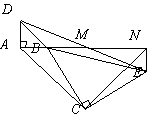
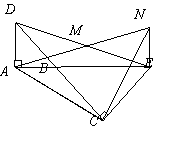
如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．

（1）当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；

（2）将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；

（3）将图1中△BCE绕点B旋转到图3位置，此时A，B，M三点在同一直线上．（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．

25．（2017天门数学）（本题满分12分）

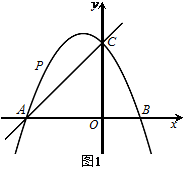
在平面直角坐标系中，抛物线与轴交于点A，B，与轴交于点C，直线经过A，C两点．

（1）求抛物线的解析式；

（2）在AC上方的抛物线上有一动点．

①如图1，当点P运动到某位置时，以AP，AO为邻边的平行四边形第四个顶点恰好也在抛物线上，求出此时点的坐标；

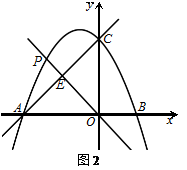
②如图2，过点O，P的直线交AC于点E，若，求的值．