湖北省神农架市2017年中考数学试题
一、选择题:本大题共15个小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.有理数![]() 的倒数为( )
的倒数为( )
A. 5 B.![]() C.
C.![]() D.
D.![]()
2.如下字体的四个汉字中,是轴对称图形的是( )
A.![9U1]~JN[(%JKO8H6CW%Z@0X](http://img.chusan.com/upLoad/doc2017/lbx44oh8/181736.004.png) B.
B.![ZT0)YRT9RY`{Q]`D[JPVZ2E](http://img.chusan.com/upLoad/doc2017/lbx44oh8/181736.005.png) C.
C. D.
D.
3.(2017神农架数学试题)如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“爱”字一面的相对面上的字是( )
![[E$7~2JUFJ6XMLB0E{5]8HE](http://img.chusan.com/upLoad/doc2017/lbx44oh8/181736.008.png)
A.美 B.丽 C.宜 D. 昌
4.谜语:干活两腿脚,一腿勤,一腿懒,一脚站,一脚转.打一数学学习用具,谜底为( )
A.量角器 B.直尺 C. 三角板 D.圆规
5. 5月18 日,新平社电讯:我国利用世界唯一的“蓝鲸1号”,在南海实观了可燃冰(即天然气水合物)的安全可控开采.据介绍,“蓝鲸1号”拥有27354台设备,约40000根管路,约50 000个![]() 报验点,电缆拉放长度估计1200千米.其中准确数是( )
报验点,电缆拉放长度估计1200千米.其中准确数是( )
A.27354 B.40000 C.50000 D.1200
6.(2017神农架数学试题)九一(1)班在参加学校![]() 接力赛时,安排了甲,乙,丙,丁四位选手,他们的顺序由抽签随机决定,则甲跑第一棒的概率为( )
接力赛时,安排了甲,乙,丙,丁四位选手,他们的顺序由抽签随机决定,则甲跑第一棒的概率为( )
A. 1 B.![]() C.
C. ![]() D.
D.![]()
7.下列计算正确的是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
8.(2017神农架数学试题)如图,在![]() 中,尺规作图如下:分别以点
中,尺规作图如下:分别以点![]() ,点
,点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() 两点,作直线
两点,作直线![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

A.![]() 平分
平分 ![]() B.
B.![]() 垂直平分
垂直平分![]()
C. ![]() 垂直平分
垂直平分![]() D.
D.![]() 平分
平分![]()
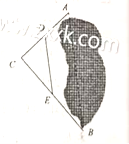
9.(2017神农架数学试题)如图,要测定被池塘隔开的![]() 两点的距离.可以在
两点的距离.可以在![]() 外选一点
外选一点![]() ,连接
,连接![]() ,并分别找出它们的中点
,并分别找出它们的中点![]() , 连接
, 连接![]() D.现测得
D.现测得![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
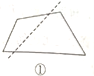
10.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )
![]()
![D]S)Y_D6ZL@TCYVMFQPN[OW](http://img.chusan.com/upLoad/doc2017/lbx44oh8/181736.050.png)
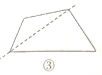
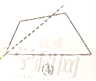
A.①② B.①③ C. ②④ D.③④
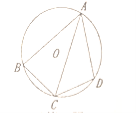
11.(2017神农架数学试题)如图,四边形![]() 内接
内接![]() ,
,![]() 平分
平分![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.(2017神农架数学试题)今年5月21日是全国第27个助残日,某地开展“心手相连,共浴阳光”为主题的手工制品义卖销售活动.长江特殊教育学校将同学们手工制作的手串、中国结、手提包、木雕笔筒的相关销售信息汇总如下表,其中销售率最高的是( )
![IZYQUYIWTKE70X89(]FFRY3](http://img.chusan.com/upLoad/doc2017/lbx44oh8/181736.062.png)
A.手串 B.中国结 C. 手提包 D.木雕笔筒
13.![]() 在网格中的位置如图所示(每个小正方体边长为1),
在网格中的位置如图所示(每个小正方体边长为1),![]() 于
于![]() ,下列选项中,错误的是( )
,下列选项中,错误的是( )
![5H89O{CUBSJN4JW]$HP4@Q5](http://img.chusan.com/upLoad/doc2017/lbx44oh8/181736.066.png)
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
14.计算![]() 的结果为( )
的结果为( )
A.1 B.![]() C.
C.![]() D.0
D.0
15.某学校要种植一块面积为100![]() 的长方形草坪,要求两边长均不小于5
的长方形草坪,要求两边长均不小于5![]() ,则草坪的一边长为
,则草坪的一边长为![]() (单位:
(单位:![]() )随另一边长
)随另一边长![]() (单位:
(单位:![]() )的变化而变化的图象可能是( )
)的变化而变化的图象可能是( )
A.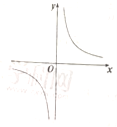 B.
B.![6]M8SW_JPQICU0I1%UIMEJ0](http://img.chusan.com/upLoad/doc2017/lbx44oh8/181736.080.png) C.
C. 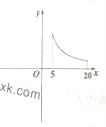 D.
D. ![P}@LN][X0B1_T185P2TAQ58](http://img.chusan.com/upLoad/doc2017/lbx44oh8/181736.082.png)
二、解答题 (本大题共9小题,共75分.解答应写出文字说明、证明过程或演算步骤.)
16.计算:![]()
17.解不等式组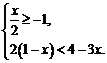
18.![]() 市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
![5WCVD)J]WKHS`Q4}IL$H(8C](http://img.chusan.com/upLoad/doc2017/lbx44oh8/181736.086.png)
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00 :需要租用公共自行车的人数是多少?
19.(2017神农架数学试题)“和谐号”火车从车站出发,在行驶过程中速度![]() (单位:
(单位:![]() )与时间
)与时间![]() (单位:
(单位:![]() )的关系如图所示,其中线段
)的关系如图所示,其中线段![]() 轴.
轴.
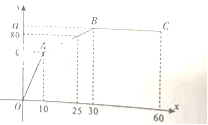
(1)当![]() ,求
,求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)求![]() 点的坐标.
点的坐标.
20.阅读:能够成为直角三角形三条边长的三个正整数![]() ,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:
,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:
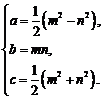 其中
其中![]() ,
,![]() 是互质的奇数.
是互质的奇数.
应用,当![]() 时,求有一边长为5的直角三角形的另外两条边长.
时,求有一边长为5的直角三角形的另外两条边长.
21.已知,四边形![]() 中,
中,![]() 是对角线
是对角线![]() 上一点,
上一点,![]() ,以
,以![]() 为直径的
为直径的![]() 与边
与边![]() 相切于点
相切于点![]() .
.![]() 点在
点在![]() 上,连接
上,连接![]() .
.
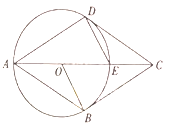
(1)求证:![]() ;
;
(2)若![]() ,求证:四边形
,求证:四边形![]() 是菱形.
是菱形.
22.(2017神农架数学试题)某市总预算![]() 亿元用三年时间建成一条轨道交通线.轨道交通线由线路敷设、搬迁安置、辅助配套三项工程组成.从2015年开始,市政府在每年年初分别对三项工程进行不同数额的投资.
亿元用三年时间建成一条轨道交通线.轨道交通线由线路敷设、搬迁安置、辅助配套三项工程组成.从2015年开始,市政府在每年年初分别对三项工程进行不同数额的投资.
2015年年初,对线路敷设、搬迁安置的投资分别是辅助配套投资的2倍、4倍.随后两年,线路敷设投资每年都增加![]() 亿元,预计线路敷设三年总投资为54亿元时会顺利如期完工;搬迁安置投资从2016年初开始遂
亿元,预计线路敷设三年总投资为54亿元时会顺利如期完工;搬迁安置投资从2016年初开始遂
年按同一百分数递减,依此规律,在 2017年年初只需投资5亿元,即可顺利如期完工;辅助配套工程在2016年年初的投资在前一年基础上的增长率是线路敷设2016年投资增长率的1.5倍,2017年年初的投资比该项工程前两年投资的总和还多4亿元,若这样,辅助配套工程也可以如期完工.经测算,这三年的线路敷设、辅助配套工程的总投资资金之比达到3: 2.
(1)这三年用于辅助配套的投资将达到多少亿元?
(2)市政府2015年年初对三项工程的总投资是多少亿元?
(3)求搬迁安置投资逐年递减的百分数.
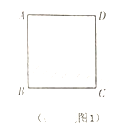
23. (2017神农架数学试题)正方形![]() 的边长为1,点
的边长为1,点![]() 是
是![]() 边上的一个动点(与
边上的一个动点(与![]() 不重合),以
不重合),以![]() 为顶点在
为顶点在![]() 所在直线的上方作
所在直线的上方作![]() .
.
(1)当![]() 经过点
经过点![]() 时,
时,
①请直接填空:![]() (可能,不可能)过
(可能,不可能)过![]() 点;(图1仅供分析)
点;(图1仅供分析)
②如图2,在![]() 上截取
上截取![]() ,过
,过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,册
,册![]() 于
于![]() ,求证:四边形
,求证:四边形![]() 为正方形.
为正方形.
(2)当![]() 不过点
不过点![]() 时,设
时,设![]() 交边
交边![]() 于
于![]() ,且
,且![]() .在
.在![]() 上存在点
上存在点![]() ,过
,过![]() 点作
点作![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,使得
,使得![]() ,连接
,连接![]() ,求四边形
,求四边形![]() 的最大面积.
的最大面积.
![JQJ]FXAX89GLZVY7L3UU{)5](http://img.chusan.com/upLoad/doc2017/lbx44oh8/181736.153.png)

24.已知抛物线![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)直接写出关于![]() 的一元二次方程
的一元二次方程![]() 的一个根;
的一个根;
(2)证明:抛物线![]() 的顶点
的顶点![]() 在第三象限;
在第三象限;
(3)直线![]() 与
与![]() 轴分别相交于
轴分别相交于![]() 两点,与抛物线
两点,与抛物线![]() 相交于
相交于![]() 两点.设抛物线
两点.设抛物线![]() 的对称轴与
的对称轴与![]() 轴相交于
轴相交于![]() ,如果在对称轴左侧的抛物线上存在点
,如果在对称轴左侧的抛物线上存在点![]() ,使得
,使得![]() 与
与![]() 相似.并且
相似.并且![]() ,求此时抛物线的表达式.
,求此时抛物线的表达式.

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...