请点击全屏查看
 湖北省咸宁市2017年初中毕业生学业考试
湖北省咸宁市2017年初中毕业生学业考试
数学试卷
第Ⅰ卷(共24分)
一、选择题:本大题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 下表是我市四个景区今年![]() 月份某天
月份某天![]() 时气温,其中气温最低的景区是( )
时气温,其中气温最低的景区是( )
景区 | 潜山公园 | 陆水湖 | 隐水洞 | 三湖连江 |
气温 |
|
|
|
|
A.潜山公园 B.陆水湖 C.隐水洞 D.三湖连江
2. (2017咸宁数学)在绿满鄂南行动中,咸宁市计划![]() 年至
年至![]() 年三年间植树造林
年三年间植树造林![]() 亩,全力打造绿色生态旅游城市,将
亩,全力打造绿色生态旅游城市,将![]() 用科学计数法表示为()
用科学计数法表示为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列算式中,结果等于![]() 的是()
的是()
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
4. 如图是某个几何体的三视图,该几何体是()
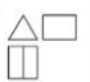
A.三棱柱 B.三棱锥 C.圆柱 D.圆锥
5. (2017咸宁数学)由于受![]() 禽流感的影响,我市某城区今年
禽流感的影响,我市某城区今年![]() 月份鸡的价格比
月份鸡的价格比![]() 月份下降
月份下降![]() ,
,![]() 月份比
月份比![]() 月份下降
月份下降![]() ,已知
,已知![]() 月份鸡的价格为
月份鸡的价格为![]() 元/千克,设
元/千克,设![]() 月份鸡的价格为
月份鸡的价格为![]() 元/千克,则()
元/千克,则()
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
6. 已知![]() 为常数,点
为常数,点![]() 在第二象限,则关于
在第二象限,则关于![]() 的方程
的方程![]() 根的情况是()
根的情况是()
A.有两个相等的实数根 B.有两个不相等的实数根 C.没有实数根 D.无法判断
7. 如图,⊙![]() 的半径为
的半径为![]() ,四边形
,四边形![]() 内接于⊙
内接于⊙![]() ,连接
,连接![]() ,若
,若![]() ,则
,则![]() 的长为()
的长为()
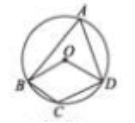
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
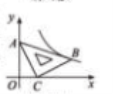
8. (2017咸宁数学)在平面直接坐标系![]() 中,将一块含义
中,将一块含义![]() 角的直角三角板如图放置,直角顶点
角的直角三角板如图放置,直角顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 恰好落在第一象限的双曲线上,现将直角三角板沿
恰好落在第一象限的双曲线上,现将直角三角板沿![]() 轴正方向平移,当顶点
轴正方向平移,当顶点![]() 恰好落在该双曲线上时停止运动,则此点
恰好落在该双曲线上时停止运动,则此点![]() 的对应点
的对应点![]() 的坐标为()
的坐标为()
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
第Ⅱ卷(共96分)
二、填空题(每题8分,满分24分,将答案填在答题纸上)
9. ![]() 的立方根是 .
的立方根是 .
10. 化简:![]() .
.
11. 分解因式:![]() .
.
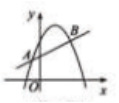
12. (2017咸宁数学)如图,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,则关于
两点,则关于![]() 的不等式
的不等式![]() 的解集是 .
的解集是 .
13. 小明的爸爸是个“健步走”运动爱好者,他用手机软件记录了某个月(![]() 天)每天健步走的步数,并将记录结果绘制成了如下统计表:
天)每天健步走的步数,并将记录结果绘制成了如下统计表:
步数(万步) |
|
|
|
|
|
天数 |
|
|
|
|
|
在每天所走的步数这组数据中,众数和中位数分别是 .
14.(2017咸宁数学) 如图,点![]() 的矩形纸片
的矩形纸片![]() 的对称中心,
的对称中心,![]() 是
是![]() 上一点,将纸片沿
上一点,将纸片沿![]() 折叠后,点
折叠后,点![]() 恰好与点
恰好与点![]() 重合,若
重合,若![]() ,则折痕
,则折痕![]() 的长为 .
的长为 .
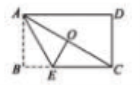
15. 如图,边长为![]() 的正六边形
的正六边形![]() 的中心与坐标原点
的中心与坐标原点![]() 重合,
重合,![]() 轴,将正六边形
轴,将正六边形![]() 绕原点
绕原点![]() 顺时针旋转
顺时针旋转![]() 次,每次旋转
次,每次旋转![]() ,当
,当![]() 时,顶点
时,顶点![]() 的坐标为 .
的坐标为 .
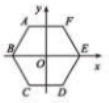
16.(2017咸宁数学) 如图,在![]() 中,
中,![]() ,斜边
,斜边![]() 的两个端点分别在相互垂直的射线
的两个端点分别在相互垂直的射线![]() 上滑动,下列结论:
上滑动,下列结论:
①若![]() 两点关于
两点关于![]() 对称,则
对称,则![]() ;
;
②![]() 两点距离的最大值为
两点距离的最大值为![]() ;
;
③若![]() 平分
平分![]() ,则
,则![]() ;
;
④斜边![]() 的中点
的中点![]() 运动路径的长为
运动路径的长为![]() .
.
其中正确的是 .
三、解答题 (本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
17. ⑴计算:![]() ;⑵解方程:
;⑵解方程:![]() .
.
18. 如图,点![]() 在一条直线上,
在一条直线上,![]() .
.
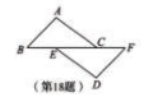
⑴求证:![]() ;
;
⑵连接![]() ,求证:四边形
,求证:四边形![]() 是平行四边形.
是平行四边形.
19. (2017咸宁数学)咸宁市某中学为了解本校学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况,随机抽取了部分学生进行问卷调查,根据调查结果绘制了如下图所示的两幅不完整统计图,请你根据图中信息解答下列问题:
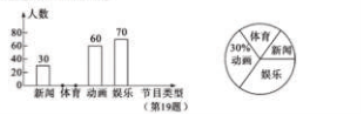
⑴补全条形统计图,“体育”对应扇形的圆心角是 度;
⑵根据以上统计分析,估计该校![]() 名学生中喜爱“娱乐”的有 人;
名学生中喜爱“娱乐”的有 人;
⑶在此次问卷调查中,甲、乙两班分别有![]() 人喜爱新闻节目,若从这
人喜爱新闻节目,若从这![]() 人中随机抽取
人中随机抽取![]() 人去参加“新闻小记者”培训,请用列表法或者画树状图的方法求所抽取的
人去参加“新闻小记者”培训,请用列表法或者画树状图的方法求所抽取的![]() 人来自不同班级的概率
人来自不同班级的概率
20.(2017咸宁数学) 小慧根据学习函数的经验,对函数![]() 的图象与性质进行了研究,下面是小慧的研究过程,请补充完成:
的图象与性质进行了研究,下面是小慧的研究过程,请补充完成:
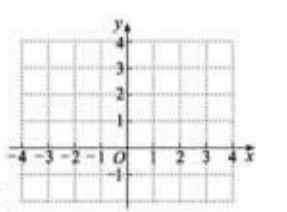
⑴函数![]() 的自变量
的自变量![]() 的取值范围是 ;
的取值范围是 ;
⑵列表,找出![]() 与
与![]() 的几组对应值.
的几组对应值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ;
;
⑶在平面直角坐标系![]() 中,描出以上表中各队对应值为坐标的点,并画出该函数的图象;
中,描出以上表中各队对应值为坐标的点,并画出该函数的图象;
⑷写出该函数的一条性质: .
21.(2017咸宁数学) 如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的⊙
为直径的⊙![]() 与边
与边![]() 分别交于
分别交于![]() 两点,过点
两点,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
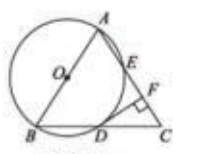
⑴求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
⑵若![]() ,求
,求![]() 的长
的长
22.(2017咸宁数学) 某公司开发出一款新的节能产品,该产品的成本价位![]() 元/件,该产品在正式投放市场前通过代销点进行了为期一个月(
元/件,该产品在正式投放市场前通过代销点进行了为期一个月(![]() 天)的试销售,售价为
天)的试销售,售价为![]() 元/件.工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线
元/件.工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线![]() 表示日销售量
表示日销售量![]() (件)与销售时间
(件)与销售时间![]() (天)之间的函数关系,已知线段
(天)之间的函数关系,已知线段![]() 表示的函数关系中,时间每增加
表示的函数关系中,时间每增加![]() 天,日销售量减少
天,日销售量减少![]() 件.
件.
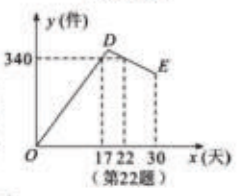
⑴第![]() 天的日销售量是 件,日销售利润是 元;
天的日销售量是 件,日销售利润是 元;
⑵求![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围;
的取值范围;
⑶日销售利润不低于![]() 元的天数共有多少天?试销售期间,日销售最大利润是多少元?
元的天数共有多少天?试销售期间,日销售最大利润是多少元?
23(2017咸宁数学).定义:
数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.
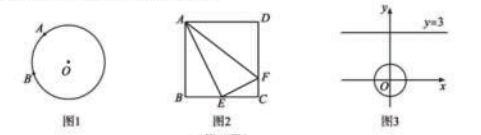
理解:
⑴如图![]() ,已知
,已知![]() 是⊙
是⊙![]() 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点![]() ,使
,使![]() 为“智慧三角形”(画出点
为“智慧三角形”(画出点![]() 的位置,保留作图痕迹);
的位置,保留作图痕迹);
⑵如图![]() ,在正方形
,在正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,且
上一点,且![]() ,试判断
,试判断![]() 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;
运用:
⑶如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,⊙
中,⊙![]() 的半径为
的半径为![]() ,点
,点![]() 是直线
是直线![]() 上的一点,若在⊙
上的一点,若在⊙![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为“智慧三角形”,当其面积取得最小值时,直接写出此时点
为“智慧三角形”,当其面积取得最小值时,直接写出此时点![]() 的坐标.
的坐标.
24.(2017咸宁数学)如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其对称轴交抛物线于点
,其对称轴交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,已知
,已知![]() .
.

⑴求抛物线的解析式及点![]() 的坐标;
的坐标;
⑵连接![]() 为抛物线上一动点,当
为抛物线上一动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
⑶平行于![]() 轴的直线交抛物线于
轴的直线交抛物线于![]() 两点,以线段
两点,以线段![]() 为对角线作菱形
为对角线作菱形![]() ,当点
,当点![]() 在
在![]() 轴上,且
轴上,且![]() 时,求菱形对角线
时,求菱形对角线![]() 的长.
的长.


![]()

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...