2018年忻州中考数学押题卷word版（含答案）

各位同学在查看时请点击全屏查看

2018年忻州中考数学押题卷

题型一数学问题

1. 《九章算术》方程问题：“五只雀、六只燕，共重1斤（等于16两），雀重燕轻．互换其中一只，恰好一样重．问：每只雀、燕的重量各为多少？”它涉及的数学问题是（）

A.一元一次方程B.二元一次方程组

C.一元二次方程D.分式方程

2. “引葭赴岸”是《九章算术》中的一道题：“今有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐．问水深，葭长各几何？”题意是：有一个边长为1O尺的正方形池塘，一棵芦苇生长在它的中央，高出水面为l尺．如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部恰好碰到岸边的（如图）．问水深和芦苇长各多少？它涉及的数学问题是 ( )

A.勾股定理

B一次函数

C.一元一次方程的实际应用

D.二元一次方程的实际应用

题型二 数学思想

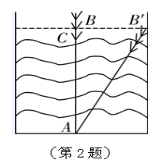
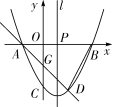
1.问题：“如图，已知点在直线上，以线段为一边画等腰三角形，且使另一顶点在直线上，则满足条件的点有几个？”．我们可以用圆规探究，按如图的方式，画图找到4个点：、、、．这种问题说明的方式体现的数学思想是 （）

A．归纳与演绎

B．分类讨论

C．数形结合

D．转化与化归

2. “已知二次函数的图象如图所示，试判断与0的大小．”一同学是这样回答的：“由图象可知：当时＜0，所以＜0．”他这种说明问题的方式体现的数学思想方法叫做

（ ）

A．换元法

B．配方法

C．数形结合法

D．分类讨论法

题型三 跨学科试题

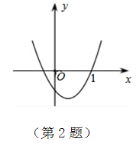
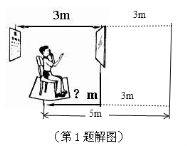
1. 视力检测时要求被测的人与视力表的距离为5 m．如图所示，视力表与平面镜的距离是3 m．为满足测量要求，人与平面镜的距离应为 （）

A．1 m B．1.5 mC．2 mD．2.5 m

2. 我国自主研制的载人潜水器“蛟龙号”下潜深度已突破7 km.为估算“蛟龙号”下潜到m深度处所受海水的压强p，可取海水的密度为kg/m3,g取10 N/kg，根据p =ρgh，那么用科学记数法表示出p为 .

重难点题型猜押

命题点一 图形操作题

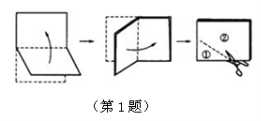
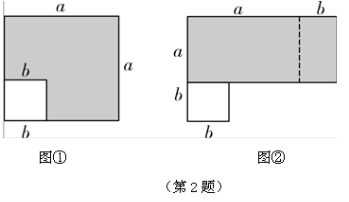
1.将一张矩形纸按照如图方式对这两次后，沿着图中的虚线剪开，得到、两部分，将展开后得到的平面图形是（ ）

1. 直角三角形B.矩形 C.正方形D.菱形

2. 如图，在边长为a的正方形中挖去一个边长为b的小正方形（a＞b），再把剩余的部分剪拼成一个矩形，通过计算图形（阴影部分）的面积，验证了一个等式是 .

命题点二规律探索题

1. 如图，下列图形都是由火柴棒所搭成的图形，第一个图形有3根火柴棒，第二个图形有5根火柴棒，第三个图形有7根火柴棒，…，按此规律，则第九个图形所需火柴棒的根数是（）

（第1题）

A.17 B.18 C.19 D.20

2.下列图形都是由同样大小的黑点按一定的规律组成，其中第个图形中一共有4个黑点，第个图形中一共有9个黑点，第个图形中一共有14个黑点，…，则第⑩个图形中黑点的个数是 （）

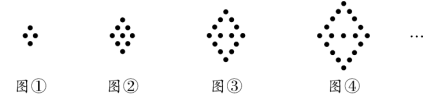
（第2题）

A.44B.48C.49 D.54

3. 已知我们定义：根据你观察的规律可推测出= .

命题点三 阴影部分面积计算

1. 如图，四边形是菱形，=60°，,扇形的半径为1，圆心角为60°，则图中阴影部分的面积是 .

2. 如图，△绕点顺时针旋转45°得到△，若∠=90°，== ，求图中阴影部分的面积为 .

命题点四猜想证明题

1. 问题情境： 如图①，在Rt△中，,点为直线上一点（点不与,重合），以为边作正方形(、、、按逆时针排列)，连接.

初步探究：（1）如图①，当点在边上时，求证：①；②⊥；

解决问题：（2）如图②，当点在边的延长线上且其他条件不变时，线段与的上述关系是否成立？请直接写出结论（不必写证明过程）；

类比延伸：（3）如图③，当点在边的延长线上且其他条件不变时，且点、在直线的两侧，其他条件不变，线段线段与的上述关系是否成立？若成立，请证明你的结论；若不成立，请说明理由.

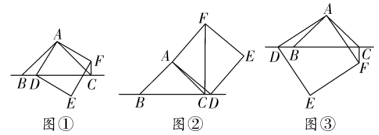
（第1题）

2. 课题学习：三角形中两条线段之间的数量关系.

问题情境：数学活动课上，老师提出了一个问题：已知△是等边三角形，是边上一动点（点不与点,重合），在边的延长线上，连接、.使.如图①，若是边的中点时.试猜想线段与的数量关系.

（1）独立思考：请解答老师提出的问题；

（2）提出问题：一小组受此问题的启发，提出问题，如图②，若点是线段上的任意一点，其他条件不变，则线段、之间有什么数量关系？请解决该小组提出的问题，并给出证明；

（3）问题拓展：老师要求其他小组向一小组同学学习，仿照前两种情况提出问题，二小组提出问题：如图③，若是线段延长线上的任意一点，其他条件不变，则线段、之间有什么数量关系？任务：请解答二小组所提出的问题，不必证明？

（第2题）

名校模拟题

命题点一 数学问题与数学思想

1.如图，“毕达哥拉斯树”是由毕达哥拉斯画出来的一个可以无限延展的图形，这一图形反映的数学原理是（ ）

1. 黄金分割 B.勾股定理

C.平行线分线段成比例 D.垂径定理

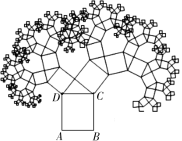
（第1题）

命题点二 跨学科试题

1. 已知在1标准大气压下，1的水温度升高1℃需要吸收4200J的热量，在同样的条件下，10的水温度由50℃升高到100℃所吸收的热量用科学记数法表示为（ ）

1. JB.J C.J D.J

2.阅读材料：以下是我们教科书中的一段内容，请仔细阅读，并解答有关问题.公元前3世纪，古希腊科学家阿基米德发现：若杠杆上的两物体与支点的距离与其重量成反比，则杠杆平衡.后来，人们把它归纳为“杠杆原理”，通俗地说，杠杆原理为：阻力×阻力臂=动力×动力臂（如图）.

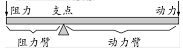
图① 图②

（第2题）

问题解决：

若工人师傅欲用撬棍撬动一块大石头，已知阻力和臂力不变，分别为1500 N和0.4 m.

(1)动力F（N）与动力臂（m）有怎样的函数关系？当动力臂是1.5 m时，撬动石头需要多大的力？

（2）若想使动力F（N）不超过题（1）中所用力的一半，则动力臂至少要加长多少？

数学思考：

（3）请用数学知识解释：我们使用撬棍，当阻力与阻力臂一定时，为什么动力臂越长越省力.

命题点三 尺规作图

1. 如图，已知△ABC.

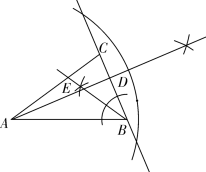
（1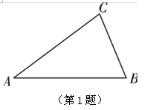）实践与操作： 利用尺规按下列要求作图吧，并在图中标明相应的字母（保留作图痕迹，不写作法）.

作BC边上的高AD ；

作△ABC的角平分线BE ；

（2）综合与运用：

若△ABC中AB=AC且∠CAB=36，请根据作图和已知写出符合括号内要求的正确结论：

结论1：____________________________;（关于角）

结论2：____________________________;（关于线段）

结论3：____________________________.（关于三角形）

2. 如图，已知△ABC .

（1）实践与操作：利用尺规按下列要求作图，并在图中标明相应的字母（保留作图痕迹，不写作法）.

作∠A的平分线AD，交BC与点E；

经过点B作AD的垂线交AD于点F；

连接CF.

（2）综合与应用：

若△ABC是直角三角形，∠ABC=°，AB =3，BC =4，则△ACF的面积是______.

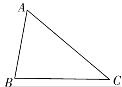
（第2题）

命题点四 猜想证明题

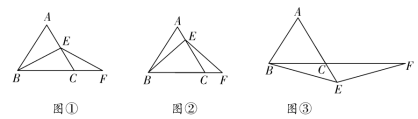
1.问题情景：

1节数学课后，老师布置了一道课后练习题：

如图，已知在Rt△ABC中，AC =BC，∠ACB =90°，CD⊥AB于点D ，点E、点F分别在AD和BC上，∠1=∠2，FG⊥AB于点G，求证：△CDE≌△EGF.

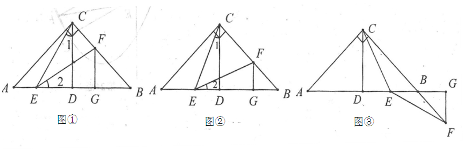
（第1题）

（1）阅读理解，完成解答：本题证明的思路可用下列框图表示：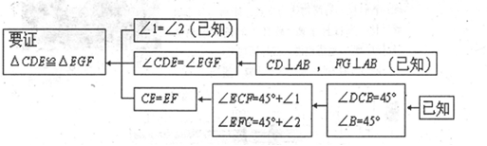

根据上述思路，请你完整地书写这道练习题的证明过程;

（2）特殊位置，证明结论：如图②，若CE平分∠ACD，其余条件不变，判断AE和BF的数量关系，并说明理由；

（3）知识迁移，探究发现：如图③，已知Rt△ABC中，AC =BC，

∠ACB =90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上，且EC =EF，请直接写出BF与AE的数量关系.（不必写解答过程）

命题点五函数动态探究题

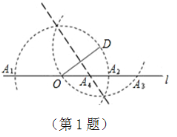
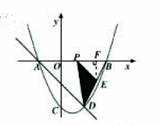
1.如图，已知二次函数的图象与轴交于A，B两点，（点A在点B左侧），与轴交于点C，点A的坐标为（-2,0）且当=-1和=3时二次函数的值相等，直线AD交抛物线于点D（2，m）.

（1）求二次函数的表达式；

（2）点P是线段AB上的一动点（点P和点A，B不重合），过点P作PE∥AD交BD于E，连接DP，当△DPE的面积最大时，求点P的坐标；

（3）若直线AD与轴交于点G，点M是抛物线对称轴上的动点，点N是轴上的动点，当四边形CMNG的周长最小时，求出周长的最小值和点M，点N的坐标.

(第1题)（备用图）

2018年忻州中考数学押题卷参考答案

特殊题型猜押

题型一数学问题

【答案】1.B2.A

题型二 数学思想

【答案】1.B2.C

题型三 跨学科试题

【答案】1.C【解析】 已知视力检测时要求被测的人与视力表的距离为5 m，但房间空间太小，可利用平面镜成像特点，人与视力表的像的距离为5 m，如解图所示：因为视力表距平面镜3 m所以视力表在平面镜中所成的像距离平面镜为3 m，所以人距平面镜应为5 m-3 m=2 m．

2. Pa 【解析】p =ρgh=kg/m3×10 N/kg×7000 m=

Pa .

重难点题型猜押

命题点一 图形操作题

【答案】1.D

2.a2-b2=（a+b）（a-b）【解析】左边图形中，阴影部分的面积=a2-b2，右边图形中，阴影部分的面积=（a +b）（a -b），∵两个图形中的阴影部分的面积相等，∴a2-b2=（a +b）（a -b）．

命题点二规律探索题

【答案】1.C【解析】第一个图形火柴棒的根数为2×1+1=3，第二个图形火柴棒的根数为2×2+1=5，第三个图形火柴棒的根数为2×3+1=7，第四个图形火柴棒的根数为2×4+1=9，由此可得第n个图形火柴棒的根数为2n+1，第九个图形火柴棒的根数为2×9+1=19.

2.C【解析】观察图形知：第个图形有5×（1+1）－6=4个黑点，第个图形有5×（2+1）－6=9个黑点，第个图形有5×（3+1）－6=14个黑点，第④个图形有5×（4+1）－6=19个黑点，，第n个图形有5×（n+1）－6=5n-1个黑点.当n =10时，有5×10－1=49个黑点.

3. 【解析】

，，，...，.

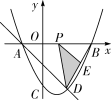
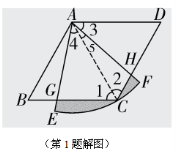
命题点三阴影部分面积计算

【答案】1.【解析】如解图，连接,∵四边形是菱形，∵=60°，,=120°，

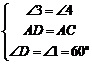∴=60°，∴△、△都是等边三角形，∴,∴△的高为，∵扇形的半径为1，圆心角为60°，∴=60°，∴，设、相交于点,、相交于点,在△和△中，,∴△≌△(ASA),

∴四边形的面积等于△的面积，∴图中阴影部分的面积是

S扇形AEF－ S△ACD.

2.【解析】∵=90°，,∴=45°，∵△绕点顺时针旋转45°得到△，∴=45°，=45°，,∴△为等腰直角三角形，=90°,∴=,，

,=45°，∴△和△都是等腰三角形，∴,,∴S阴影=S△ADB － S△BE

=.

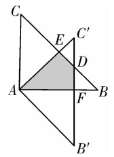
（第2题解图）

命题点四猜想证明题

【答案】1.(1)证明：①∵△是等腰直角三角形，

∴,=90°，

∵四边形为正方形，

∴,

∵=90°，

∴，

即，

∴△≌△，

∴；

②由①知=45°，,

∴=45°+45°=90°，

∴⊥.

（2）解：线段与的上述关系成立，即，⊥.

（3）解：线段与的上述关系成立.

理由如下：同理可证△≌△，

∴，=180°-45°=135°，

∵=45°，

∴=135°－45°=90°，

∴⊥.

2. 解：(1).

【解法提示】∵△是等边三角形，是线段的中点，

∴=30°，,

∵，

∴，

∴，

∵==60°，

∴=30°，

∴，

∴；

（2）猜想.

证明：如解图①，过点作∥交于点，

∵△是等边三角形，

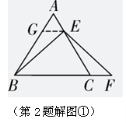∴，=60°，

又∵∥，

∴，，

又∵，

∴，

在△和△中，

，

∴△≌△（SAS），

∴；

（3）.

【解法提示】如解图②，过点作∥交延长线于点，

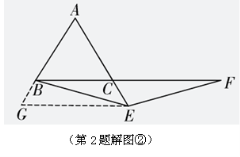∵△是等边三角形，

∴，=60°，

又∵∥，

∴=60°，

又∵=60°，

∴△是等边三角形，

∴，，

又∵，

∴，

又∵=60°，

∴在△和△中，

，

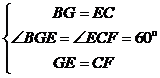∴△≌△（SAS），

∴.

名校模拟题

命题点一 数学问题与数学思想

【答案】B

命题点二 跨学科试题

【答案】1.C

2.解：（1）根据“杠杆定律”有=1500×0.4,

函数解析式为，

当等于1.5时，（N）,

因此，撬动石头需要400 N的力.

（2）由（1）可知

函数解析式为,

当时，(m).

.

因此，若用力不超过400N的一半，则动力臂至少要加长1.5m.

（3）因为撬棍工作遵循“杠杆定律”，当阻力与阻力臂一定时，其乘积为常数.设其为k,则动力F与臂力的函数关系式为，根据反比例函数的性质可知，动力F随动力臂的增大而减小，所以动力臂越长越省力.

命题点三 尺规作图

1. 解：（1）作出线段AD如解图；

作出线段BE如解图；

(第1题解图)

（2）结论1：例如，∠C =72°，∠ABC =72°，∠C =∠ABC，∠AEB=108°等；结论2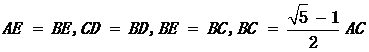：等；结论3：△ABE是等腰三角形，△BCE ∽△ABC等；

2. 解：（1）作图如解图所示.

（2）3

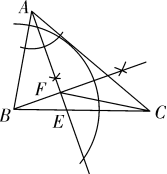
（第2题解图）

命题点四猜想证明题

1. （1）证明：∵AC =BC，∠ACB =90°，

∴∠A =∠B =45°，

∵CD⊥AB，

∴∠CDB=90°，

∴∠DCB=45°，

∵∠ECF =∠DCB +∠1=45°+∠1，∠EFC =∠B+∠2=45°+∠2，

∠1=∠2，

∴∠ECF =∠EFC，

∴CE =EF，

∵CD⊥AB，FG⊥AB，

∴∠CDE =∠EGF=90°，

在△CDE和△EGF中，

，

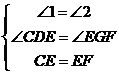∴△CDE≌△EGF（AAS）；

（2）证明：由（1）可得CE =EF，∠A=∠B，

∵CE平分∠ACD，

∴∠ACE=∠1，

∵∠1=∠2，

∴∠ACE =∠2，

在△ACE和△BEF中，

，

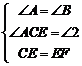∴△ACE≌△BEF(AAS)，

∴AE=BF ；

（3）.

命题点五 函数动态探究题

1. 解：（1）当=1和=3时二次函数的值相等，

∴二次函数图象的对称轴为直线=1，

又∵点A的坐标为（-2,0），

∴点B的坐标为（4,0），

∴，

解方程得，

∴二次函数的表达式为；

（2）∵点D（2，m）在抛物线上，即，

∴点D的坐标为（2，-4）.

如解图①，过点E作EF⊥PB于点F，设点P坐标为（t，0），其中，

∵PE∥AD，

∴△BEP ∽△BDA.

∴，即，

∴EF =，∴

=-，

∴当t=1时，有最大值，

∴此时点P的坐标为（1，0）.

（3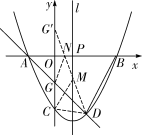）∵A（-2,0），D（2，-4），∴直线AD的表达式为，

∵当x=0时，y=-2，

∴点G的坐标为（0，-2），

∵当x=0时，二次函数的函数值y=-4，

∴点C的坐标为（0，-4），

∵点D的坐标为（2，-4），

∴点C，D关于直线x=1对称，

如解图，作点G关于x轴的对称点，即（0,2），连接D交对称轴于点M，交x轴于点N，连接DC ,CM ,GN，DC =2，C=6，∴D=，

∴CG +GN +MN +MC =CG +N +MN +MD =CG+D=2+，

∵两点之间线段最短，

∴GN+NM+MC的最小值为，

∴四边形CMNG周长的最小值为2+，

∵D（2，-4），（0,2）

∴直线D的表达式为，

∵当x=1时，y=-1；当y=0时，，

∴满足条件的点M的坐标为（1，-1），点N的坐标为（）.