2017年南昌八年级数学月考题（精编word版）

为了方便您的阅读请点击全屏查看

一．选择题（共8小题,每小题3分，共24分）

1．以下列各组线段为边，能组成三角形的是（）

A．1cm，2cm，4cm              B．2cm，3cm，5cm              C．5cm，6cm，12cm              D．4cm，6cm，8cm2．正多边形的一个内角等于144°，则该多边形是正（）边形．

A．8              B．9C．10              D．11

3．如图，AB=AD，CB=CD，∠B=30゜，∠BAD=46゜，则∠ACD的度数是（）

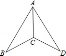
A．120゜              B．125゜              C．127゜              D．104゜4．如图，已知∠1=∠2，AC=AD，增加下列条件之一：①AB=AE；②BC=ED；③∠C=∠D；

④∠B=∠E．其中能使△ABC≌△AED的条件有（）

A．4个B．3个C．2个D．1个

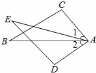
5．如图，已知AB=AC，AD=AE，∠BAC=∠DAE．下列结论不正确的是（）

A．∠BAD=∠CAEB．△ABD≌△ACE              C．AB=BCD．BD=CE

6．直线a∥b，直角三角形如图放置，若∠1+∠A=65°，则∠2的度数为（）

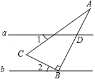
A．15°B．20°C．25°D．30°

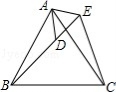
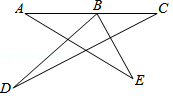
7．如图所示，若∠DBE=78°，则∠A+∠C+∠D+∠E=（）

A．102°              B．52°              C．162°              D．192°

8．如图，在△ABC中，D为AB的中点，CE=3BE，CF=2AF，四边形CEDF的面积为17，则△ABC的面积为（）

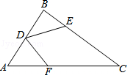
A．22B．23              C．24              D．25

二．填空题（共6小题,每小题3分，共18分）

9．已知等腰三角形的两条边长分别为2和5，则它的周长为              ．

10．若从一个多边形的一个顶点出发，最多可以引10条对角线，则它是              边形．

11．已知在△ABC中，∠A=40°，∠B﹣∠C=40°，则∠B=              ．

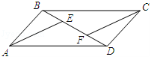
12．如图，AB∥CD，BC∥AD，AB=CD，BE=DF，则图中全等三角形有              对．

13．若A（2，0），B（0，4），C（2，4），D为坐标平面内一点，且△ABC与△ACD全等，则D点坐标为              ．

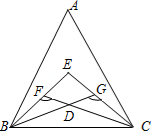
14．如图，△ABC，∠ABC、∠ACB的三等分线交于点E、D，若∠BFC=132°，∠BGC=120°，则∠E的度数为              ．

三．（共4小题，每小题6分，共24分）

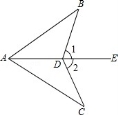
15．如图，AB=AC，BD=CD，求证：∠1=∠2．

16．已知一个多边形的内角和与外角和的差为1080°，

（1）求这个多边形的边数；（2）求此多边形的对角线条数。

17．已知：如图，AD是△ABC的高，BE平分∠ABC交AD于E，若∠C=70°，∠BED=68°，求∠BAC的度数．

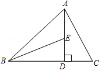
18．如图，△ABC≌△ADE，若∠B=80°，∠C=30°，∠DAB：∠DAC=4：3，求∠DAE和∠

EFC的度数。

四．（共3小题，第19,20题每题7分，第21题8分，共22分）

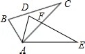
19．如图，△ABC的周长是21cm，AB=AC，中线BD分△ABC为两个三角形，且△ABD的周长比△BCD的周长大6cm，求AB，BC．

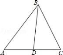
20．如图1△ABC中，H是高AD和BE的交点，且AD=BD．

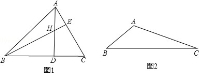
（1）请你猜想BH和AC的关系，并说明理由

（2）若将图（1）中的∠A改成钝角，其他不变，此时（1）中的结论还成立吗？请说明理由．

21．（1）已知：如图1，P为△ADC内一点，DP、CP分别平分∠ADC和∠ACD，如果∠A=60°，那么∠P=              °；如果∠A=90°，那么∠P=              °；（直接写出答案，不必说明理由）

（2）如图2，p为四边形ABCD内一点，DP、CP分别平分∠ADC和∠BCD，请直接写出∠P与∠A+∠B的数量关系：                            （直接写出答案，不必说明理由）

（3）如图3，P为五边形ABCDEF内一点，DP、CP分别平分∠EDC、∠BCD，试探究∠P与∠A+∠B+∠E的数量关系，并说明理由；

（4）若P为n边形A1A2A3…An内一点，PA1平分∠AnA1A2，PA2平分∠A1A2A3，请直接写出

∠P与∠A3+A4+A5+…+∠An的数量关系：              （用含n的代表式表示，直接写出答案，不必说明理由）

五．（共1小题，共12分）

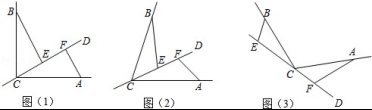
22．CD经过∠BCA顶点C的一条直线，CA=CB．E，F分别是直线CD上两点，且∠BEC=

∠CFA=α．

（1）若直线CD经过∠BCA的内部，且E，F在射线CD上，

①如图（1），若∠BCA=90°，∠α=90°，则EF，BE，AF三条线段数量关系是              .

（直接写出答案，不必说明理由）

②如图（2），若0°<∠BCA<180°,∠α+∠BCA=180°，那么①中的结论仍然成立吗？请说明理由．

（2）如图（3），若直线CD经过∠BCA的外部，且∠α=∠BCA，若BE=3，AF=5，试求出EF的长．