2018伊春市中考数学模拟试题
一、选择题
1.下列各数中,比﹣3小的数是( )
A.﹣3B.﹣2C.0D.﹣4
2.下列运算正确的是( )
A.a•a2=a3B.3a+2a2=5a2C.2﹣3=﹣8D.![]() =±3
=±3
3.在下列四个图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
B. C.
C. D.
D.
4.对于双曲线y=![]() ,当x>0时,y随x的增大而减小,则m的取值范围为( )
,当x>0时,y随x的增大而减小,则m的取值范围为( )
A.m>0B.m>1C.m<0D.m<1
5.如图是一个螺母零件的立体图形,它的左视图是( )

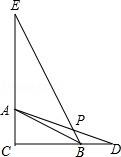
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.某纪念品原价为168元,连续两次降价a%后售价为128元,下列所列方程正确的是( )
A.160(1+a%)2=128B.160(1﹣a%)2=128C.160(1﹣2a%)=128D.160(1﹣a%)=128
7.如图,在▱ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
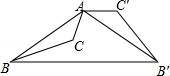
8.如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
A.55°B.65°C.75°D.85°
9.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为( )
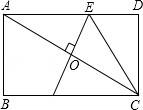
A.3B.3.5C.2.5D.2.8
10.某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,则下列说法:
①张强返回时的速度是l50米/分;
②妈妈原来的速度为50米/分;
③妈妈比按原速返回提前l0分钟到家;
④当时间为25分或33分或35分时,张强与妈妈相距l00米
正确个数为( )
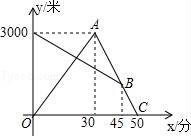
A.1个B.2个C.3个D.4个
二、填空题
11.将l 250 000 000用科学记数法表示为 .
12.在函数y=![]() 中,自变量x的取值范围是 .
中,自变量x的取值范围是 .
13.计算:![]() ﹣
﹣![]() = .
= .
14.分解因式:a3+ab2﹣2a2b= .
15.不等式组![]() 的解集是 .
的解集是 .
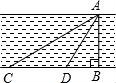
16.如图,测量河宽AB(假设河的两岸平行),在C点测得∠ACB=30°,D点测得∠ADB=60°,又CD=60m,则河宽AB为 m(结果保留根号).
17.一个扇形的圆心角为60°,它所对的弧长为2πcm,则这个扇形的半径为 cm.
18.已知,PA、PB分别切⊙O于A、B两点,∠APB=50°,C为⊙O上一点,(不与A、B重合),则∠ACB= 度.
19.不透明的布袋里有2个红色小汽车,2个白色小汽车模型(小汽车除颜色不同外,其它都相同),从布袋中随机摸出1个小汽车记下颜色后放回袋中摇匀,然后重新再摸出1个小汽车,则摸出的两个小汽车都是红色的概率是 .
20.已知,Rt△ABC中∠C=90°,点D在边CB的延长线上,BD=AC,点E在边CA的延长线上,AE=CD,连接BE、AD交于点P,若BC=2BD=2,则PE= .
三、解答题
21.先化简,再求代数式:(![]() ﹣
﹣![]() )÷
)÷![]() 的值,其中x=2+tan60°,y=4sin30°.
的值,其中x=2+tan60°,y=4sin30°.
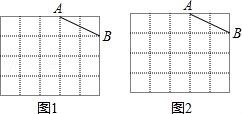
22.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A、B在小正方形的顶点上,请在图1、图2中各画一个三角形,满足以下要求:
(1)在图1中,画直角三角形ABC,点C在小正方形的顶点上,且△ABC的面积为5;
(2)在图2中,画△ABE,点E在小正方形的顶点上,△ABE有一个内角为45°,且面积为3.
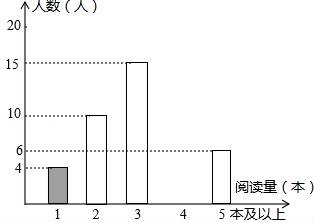
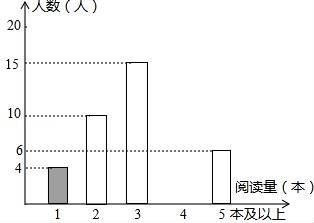
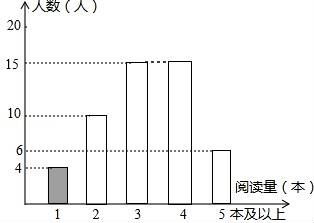
23.某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题:
(1)求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数;
(2)将条形统计图补充完整;
(3)若规定:假期阅读3本及3本以上课外书者为完成假期作业,据此估计该校1500名学生中,完成假期作业的有多少名学生?
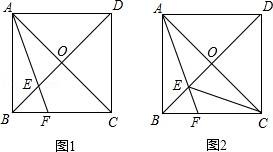
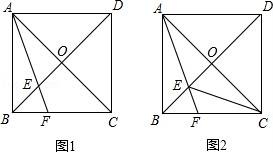
24.已知四边形ABCD是正方形,AC、BD相交于点O,过点A作∠BAC的平分线分别交BD、BC于E、F.
(1)如图1,求证:CF=2EO;
(2)如图2,连接CE,在不添加其它线的条件下,直接写出图中的等腰三角形(等腰直角三角形除外).
25.某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
26.已知,AB是⊙O的直径,AE、AF是弦,BC是⊙O的切线,过点A作AD,使∠DAF=∠AEF.
(1)如图(1),求证:AD∥BC;
(2)如图(2),若AD=BC=AB,连接CD,延长AF交CD于G,连接CF,若G为CD中点,求证:CF=CB;
(3)如图(3),在(2)的条件下,点I在线段FG上,且IF=AF,点P在![]() 上,连接BP并延长到L,使PL=PB,连接AL,延长EA、BI交于点K,已知∠BAK+∠ABL=180°,∠ABI+∠BAL=90°,⊙O的半径为
上,连接BP并延长到L,使PL=PB,连接AL,延长EA、BI交于点K,已知∠BAK+∠ABL=180°,∠ABI+∠BAL=90°,⊙O的半径为![]() ,求四边形ALBK的面积.
,求四边形ALBK的面积.
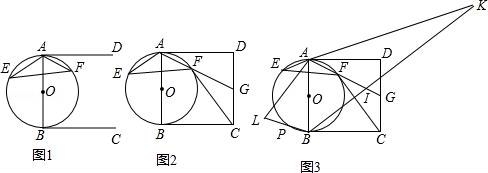
27.如图,二次函数y=ax2+bx(a≠0)的图象经过点A(1,4),对称轴是直线x=﹣![]() ,线段AD平行于x轴,交抛物线于点D.在y轴上取一点C(0,2),直线AC交抛物线于点B,连结OA,OB,OD,BD.
,线段AD平行于x轴,交抛物线于点D.在y轴上取一点C(0,2),直线AC交抛物线于点B,连结OA,OB,OD,BD.
(1)求该二次函数的解析式;
(2)设点F是BD的中点,点P是线段DO上的动点,将△BPF沿边PF翻折,得到△B′PF,使△B′PF与△DPF重叠部分的面积是△BDP的面积的![]() ,若点B′在OD上方,求线段PD的长度;
,若点B′在OD上方,求线段PD的长度;
(3)在(2)的条件下,过B′作B′H⊥PF于H,点Q在OD下方的抛物线上,连接AQ与B′H交于点M,点G在线段AM上,使∠HPN+∠DAQ=135°,延长PG交AD于N.若AN+B′M=![]() ,求点Q的坐标.
,求点Q的坐标.
2018宜春市中考数学模拟试题参考答案
一、选择题
1.下列各数中,比﹣3小的数是( )
A.﹣3B.﹣2C.0D.﹣4
【考点】有理数大小比较.
【分析】根据0大于负数,负数比较大小绝对值大的反而小,即可解答.
【解答】解:∵﹣4<﹣3<﹣2<0,
∴比﹣3小的数是﹣4,
故选:D.
2.下列运算正确的是( )
A.a•a2=a3B.3a+2a2=5a2C.2﹣3=﹣8D.![]() =±3
=±3
【考点】同底数幂的乘法;算术平方根;合并同类项;负整数指数幂.
【分析】分别利用同底数幂的乘法运算法则以及算术平方根和合并同类项法则以及负整数指数幂的性质分别化简求出答案.
【解答】解:A、a•a2=a3,正确;
B、3a+2a2无法计算,故此选项错误;
C、2﹣3=![]() ,故此选项错误;
,故此选项错误;
D、![]() =3,故此选项错误;
=3,故此选项错误;
故选:A.
3.在下列四个图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
B. C.
C. D.
D.
【考点】中心对称图形;轴对称图形.
【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.
【解答】解:A、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,也不是轴对称图形,故此选项错误;
B、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故此选项正确;
C、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,也不是轴对称图形,故此选项错误;
D、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,也不是轴对称图形,故此选项错误.
故选:B.
4.对于双曲线y=![]() ,当x>0时,y随x的增大而减小,则m的取值范围为( )
,当x>0时,y随x的增大而减小,则m的取值范围为( )
A.m>0B.m>1C.m<0D.m<1
【考点】反比例函数的性质.
【分析】根据反比例函数的单调性结合反比例函数的性质,即可得出反比例函数系数的正负,由此即可得出关于m的一元一次不等式,解不等式即可得出结论.
【解答】解:∵双曲线y=![]() ,当x>0时,y随x的增大而减小,
,当x>0时,y随x的增大而减小,
∴1﹣m>0,
解得:m<1.
故选D.
5.如图是一个螺母零件的立体图形,它的左视图是( )
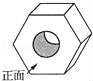
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【考点】简单组合体的三视图.
【分析】从左边看螺母零件的立体图形,确定出左视图即可.
【解答】解:如图是一个螺母零件的立体图形,它的左视图是![]() ,
,
故选D
6.某纪念品原价为168元,连续两次降价a%后售价为128元,下列所列方程正确的是( )
A.160(1+a%)2=128B.160(1﹣a%)2=128C.160(1﹣2a%)=128D.160(1﹣a%)=128
【考点】由实际问题抽象出一元二次方程.
【分析】根据题意可以列出相应的方程,从而可以解答本题.
【解答】解:由题意可得,
160(1﹣a%)2=128,
故选B.
7.如图,在▱ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是( )
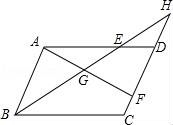
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【考点】相似三角形的判定与性质;平行四边形的性质.
【分析】由平行四边形的性质得出AB∥CD,AD∥BC,证出△ABE∽△DHE,△ABG∽△FHG,![]() ,得出对应边成比例
,得出对应边成比例![]() ,
,![]() ,即可得出结论.
,即可得出结论.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABE∽△DHE,△ABG∽△FHG,![]() ,
,
∴![]() ,
,![]() ,
,
∴选项A、B、D正确,C错误;
故选:C.
8.如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
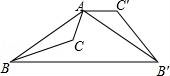
A.55°B.65°C.75°D.85°
【考点】旋转的性质;平行线的性质.
【分析】先根据旋转的性质得到∠BAB′=∠CAC′=110°,AB=AB′,根据等腰三角形的性质易得∠AB′B=35°,再根据平行线的性质得出∠C′AB′=∠AB′B=35°,然后利用∠CAB′=∠CAC′﹣∠C′AB′进行计算即可得出答案.
【解答】解:∵将△ABC绕点A按逆时针方向旋转l10°得到△AB′C′,
∴∠BAB′=∠CAC′=110°,AB=AB′,
∴∠AB′B=![]() =35°,
=35°,
∵AC′∥BB′,
∴∠C′AB′=∠AB′B=35°,
∴∠CAB′=∠CAC′﹣∠C′AB′=110°﹣35°=75°.
故选C.
9.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD、AC于点E、O,连接CE,则CE的长为( )

A.3B.3.5C.2.5D.2.8
【考点】线段垂直平分线的性质;勾股定理;矩形的性质.
【分析】根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AE=CE,设CE=x,表示出ED的长度,然后在Rt△CDE中,利用勾股定理列式计算即可得解.
【解答】解:∵EO是AC的垂直平分线,
∴AE=CE,
设CE=x,则ED=AD﹣AE=4﹣x,
在Rt△CDE中,CE2=CD2+ED2,
即x2=22+(4﹣x)2,
解得x=2.5,
即CE的长为2.5.
故选:C.
10.某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,则下列说法:
①张强返回时的速度是l50米/分;
②妈妈原来的速度为50米/分;
③妈妈比按原速返回提前l0分钟到家;
④当时间为25分或33分或35分时,张强与妈妈相距l00米
正确个数为( )
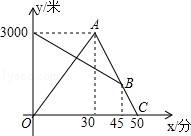
A.1个B.2个C.3个D.4个
【考点】一次函数的应用.
【分析】①根据速度=路程÷时间,即可判断;
②求出妈妈原来的速度,即可判断;
③求出妈妈原来走完3000米所用的时间,即可判断;
④分别求出张强和妈妈的函数解析式,根据张强与妈妈相距1000米,列出方程,即可判断.
【解答】解:①3000÷(50﹣30)=3000÷20=150(米/分),
所以,张强返回时的速度为150米/分,正确;
②(45﹣30)×150=2250(米),点B的坐标为(45,750),
所以,妈妈原来的速度为:2250÷45=50(米/分),正确;
③妈妈原来回家所用的时间为:3000÷50=60(分),
60﹣50=10(分),
所以,妈妈比按原速返回提前10分钟到家,正确;
④设线段BD的函数解析式为:y=kx+b,
把(0,3000),(45,750)代入得:![]() ,
,
解得:![]() ,
,
∴y=﹣50x+3000,
线段OA的函数解析式为:y=100x(0≤x≤30),
设线段AC的解析式为:y=k1x+b1,
把(30,3000),(50,0)代入得:![]() 解得:
解得:![]() ,
,
∴y=﹣150x+7500,(30<x≤50)
当张强与妈妈相距100,米时,即﹣50x+3000﹣100x=100或100x﹣(﹣50x+3000)=100或(﹣150x+7500)﹣(﹣50x+3000)=100,
解得:x=![]() 或x=
或x=![]() 或x=43,
或x=43,
所以当时间为![]() 分或
分或![]() 分或43分时,张强与妈妈何时相距100米,错误,
分或43分时,张强与妈妈何时相距100米,错误,
所以,正确的个数是3个,
故选C.
二、填空题
11.将l 250 000 000用科学记数法表示为 1.25×109 .
【考点】科学记数法—表示较大的数.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将l 250 000 000用科学记数法表示为1.25×109.
故答案为:1.25×109.
12.在函数y=![]() 中,自变量x的取值范围是 x≠﹣4 .
中,自变量x的取值范围是 x≠﹣4 .
【考点】函数自变量的取值范围.
【分析】根据分母不等于0列式计算即可得解.
【解答】解:根据题意得,x+4≠0,
解得x≠﹣4.
故答案为x≠﹣4.
13.计算:![]() ﹣
﹣![]() =
= ![]() .
.
【考点】二次根式的加减法.
【分析】先将二次根式化为最简,然后合并同类二次根式即可得出答案.
【解答】解:原式=3![]() ﹣
﹣![]() =2
=2![]() .
.
故答案为:2![]() .
.
14.分解因式:a3+ab2﹣2a2b= a(a﹣b)2 .
【考点】提公因式法与公式法的综合运用.
【分析】可先提取公因式a,再运用完全平方公式继续进行因式分解.完全平方公式:a2±2ab+b2=(a±b)2.
【解答】解:a3+ab2﹣2a2b,
=a(a2+b2﹣2ab),
=a(a﹣b)2.
15.不等式组![]() 的解集是 ﹣1≤x<3 .
的解集是 ﹣1≤x<3 .
【考点】解一元一次不等式组.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:![]() ,
,
解不等式x﹣3<0,得:x<3,
解不等式x+1≥0,得:x≥﹣1,
故不等式组的解集为:1≤x<3,
故答案为:﹣1≤x<3.
16.如图,测量河宽AB(假设河的两岸平行),在C点测得∠ACB=30°,D点测得∠ADB=60°,又CD=60m,则河宽AB为 30![]() m(结果保留根号).
m(结果保留根号).

【考点】解直角三角形的应用;勾股定理的应用.
【分析】先根据三角形外角的性质求出∠CAD的度数,判断出△ACD的形状,再由锐角三角函数的定义即可求出AB的值.
【解答】解:∵∠ACB=30°,∠ADB=60°,
∴∠CAD=30°,
∴AD=CD=60m,
在Rt△ABD中,
AB=AD•sin∠ADB=60×![]() =30
=30![]() (m).
(m).
故答案为:30![]() .
.
17.一个扇形的圆心角为60°,它所对的弧长为2πcm,则这个扇形的半径为 6 cm.
【考点】弧长的计算.
【分析】根据已知的扇形的圆心角为60°,它所对的弧长为2πcm,代入弧长公式即可求出半径r.
【解答】解:由扇形的圆心角为60°,它所对的弧长为2πcm,
即n=60°,l=2π,
根据弧长公式l=![]() ,
,
得2π=![]() ,
,
即r=6cm.
故答案为:6.
18.已知,PA、PB分别切⊙O于A、B两点,∠APB=50°,C为⊙O上一点,(不与A、B重合),则∠ACB= 65或115 度.
【考点】切线的性质.
【分析】连结OA、OB,如图,先根据切线的性质得∠PAO=∠PBO=90°,再根据四边形内角和计算出∠AOB=180°﹣∠APB=130°,然后分类讨论:当点C在优弧AB上,根据圆周角定理易得∠ACB=![]() ∠AOB;当点C在劣弧AB上,即C′的位置,根据圆内接四边形的性质易得∠AC′B=180°﹣∠ACB,问题得解.
∠AOB;当点C在劣弧AB上,即C′的位置,根据圆内接四边形的性质易得∠AC′B=180°﹣∠ACB,问题得解.
【解答】解:连结OA、OB,如图,
∵PA、PB分别切⊙O于A、B两点,
∴OA⊥PA,OB⊥PB,
∴∠PAO=∠PBO=90°,
∴∠AOB=180°﹣∠APB=180°﹣50°=130°,
当点C在优弧AB上,则∠ACB=![]() ∠AOB=65°;
∠AOB=65°;
当点C在劣弧AB上,即C′的位置,则∠AC′B=180°﹣∠ACB=180°﹣65°=115°,
即∠ACB为65°或115°.
故答案为65或115.

19.不透明的布袋里有2个红色小汽车,2个白色小汽车模型(小汽车除颜色不同外,其它都相同),从布袋中随机摸出1个小汽车记下颜色后放回袋中摇匀,然后重新再摸出1个小汽车,则摸出的两个小汽车都是红色的概率是 ![]() .
.
【考点】列表法与树状图法.
【分析】列出表格,然后根据概率公式列式计算即可得解.
【解答】解:
解:分别用红1、红2代表2个红色小汽车模型,白1、白2代表2个白色小汽车模型,
根据题意,列表如下:
| 红1 | 红2 | 白1 | 白2 |
红1 | (红1,红1) | (红1,红2) | (红1,白1) | (红1,白2) |
红2 | (红2,红1) | (红2,红2) | (红2,白1) | (红2,白2) |
白1 | (白1,红1) | (白1,红2) | (白1,白1) | (白1,白2) |
白2 | (白2,红1) | (白2,红2) | (白2,白1) | (白2,白2) |
由表可知,可能的结果共有16种,且它们都是等可能的,同时摸出的两个小汽车都是红色的有4种情况,
∴摸出的两个小汽车都是红色的概率![]() =
=![]() .
.
故答案为:![]() .
.
20.已知,Rt△ABC中∠C=90°,点D在边CB的延长线上,BD=AC,点E在边CA的延长线上,AE=CD,连接BE、AD交于点P,若BC=2BD=2,则PE= ![]() .
.

【考点】相似三角形的判定与性质;勾股定理.
【分析】过B作BH∥EC,可得△BHD∽△CAD,根据相似三角形的性质可设BP=m,则PE=9m,由勾股定理可求m,进一步求得PE的长.
【解答】解:由已知得,BC=2,BD=1,
∵BD=AC,AE=CD,
∴AE=3,AC=1,
过B作BH∥EC,
∵BH∥EC,
∴△BHD∽△CAD,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BH=![]() ,
,
∵BH∥AE,
∴△HBP∽△AEP,
∴![]() =
=![]() =
=![]() ,
,
设BP=m,则PE=9m,
∴BE=10m,
在Rt△ECB中,由勾股定理得(10m)2=22+42,
100m2=20,
m2=![]() ,
,
m=![]() ,
,
PE=![]() .
.
故答案为:![]() .
.
三、解答题
21.先化简,再求代数式:(![]() ﹣
﹣![]() )÷
)÷![]() 的值,其中x=2+tan60°,y=4sin30°.
的值,其中x=2+tan60°,y=4sin30°.
【考点】分式的化简求值;特殊角的三角函数值.
【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x与y的值代入计算即可求出值.
【解答】解:原式=![]() •
•![]() =
=![]() ,
,
当x=2+![]() ,y=4×
,y=4×![]() =2时,原式=
=2时,原式=![]() .
.
22.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A、B在小正方形的顶点上,请在图1、图2中各画一个三角形,满足以下要求:
(1)在图1中,画直角三角形ABC,点C在小正方形的顶点上,且△ABC的面积为5;
(2)在图2中,画△ABE,点E在小正方形的顶点上,△ABE有一个内角为45°,且面积为3.
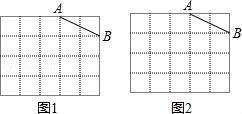
【考点】作图—复杂作图;三角形的面积;勾股定理.
【分析】(1)把AB=![]() 看作底,高为2
看作底,高为2![]() ,由此即可解决问题.
,由此即可解决问题.
(2)如图把AE=3,作为底,高为2,面积正好是3,∠E=45°满足条件.
【解答】解:(1)如图1中,△ABC即为所求.
∵∠A=90°,AC=2![]() ,AB=
,AB=![]() ,
,
∴S△ABC=![]() ×
×![]() ×
×![]() =5.
=5.
(2)如图2中,△ABE即为所求.

S△ABE=![]() ×3×2=3,∠E=45°.
×3×2=3,∠E=45°.
23.某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题:
(1)求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数;
(2)将条形统计图补充完整;
(3)若规定:假期阅读3本及3本以上课外书者为完成假期作业,据此估计该校1500名学生中,完成假期作业的有多少名学生?
【考点】条形统计图;用样本估计总体;中位数.
【分析】(1)根据阅读2本的学生有10人,占20%即可求得总人数;
(2)利用总人数50减去其它各组的人数就是读4本的学生数,据此即可作出统计图;
(3)求得样本中3本及3本以上课外书者所占的比例,然后乘以总人数1500即可求解.
【解答】解:(1)被抽查学生人数为:10÷20%=50(人),中位数是3本;
(2)阅读量为4本的人数为:50﹣4﹣10﹣15﹣6=15(人),补全条形统计图如图:
(3)![]() ×1500=1080(本),
×1500=1080(本),
答:估计该校1500名学生中,完成假期作业的有1080名学生.
24.已知四边形ABCD是正方形,AC、BD相交于点O,过点A作∠BAC的平分线分别交BD、BC于E、F.
(1)如图1,求证:CF=2EO;
(2)如图2,连接CE,在不添加其它线的条件下,直接写出图中的等腰三角形(等腰直角三角形除外).
【考点】正方形的性质;等腰三角形的判定;等腰直角三角形.
【分析】(1)取AF的中点G,连接OG,根据三角形的中位线得出OG=![]() FC,OG∥FC,根据正方形的性质求出∠OAB、∠ABO、∠OCB的度数,求出∠OEA和∠OGF的度数,推出OG=OE即可;
FC,OG∥FC,根据正方形的性质求出∠OAB、∠ABO、∠OCB的度数,求出∠OEA和∠OGF的度数,推出OG=OE即可;
(2)由已知条件和三角形内角和定理可得∠DAE=∠DEA,∠DEC=∠DCE,∠BEF=∠BFE,进而可得△DAE;△DCE;△BEF是等腰三角形,由垂直平分线的性质可得AE=CD进而可得△AEC是等腰三角形.
【解答】证明:取AF的中点G,连接OG,
∵O、G分别是AC、AF的中点,
∴OG=![]() FC,OG∥FC(三角形的中位线平行于第三边,并且等于第三边的一半),
FC,OG∥FC(三角形的中位线平行于第三边,并且等于第三边的一半),
∵正方形ABCD,
∴∠OAB=∠ABO=∠OCB=45°,
∵AF平分∠BAC,
∴∠BAF=∠OAF=22.5°,
∴∠GEO=90°﹣22.5°=67.5°,
∵GO∥FC,
∴∠AOG=∠OCB=45°,
∴∠OGE=67.5°,
∴∠GEO=∠OGE,
∴GO=OE,
∴OE=![]() FC,
FC,
即CF=2EO;
(2)
∵四边形ABCD是正方形,
∴BD⊥AC,AO=CO,∠BAC=∠DAC=45°,
∴AE=CE,
∴△AEC是等腰三角形;
∵过点A作∠BAC的平分线分别交BD、BC于E、F,
∴∠BAF=∠CAF=22.5°,
∴∠DAE=67.5°,
∴∠AED=67.5°,
∴AD=ED,
∴△ADE是等腰三角形,
∵AE=CE,
∴∠ECA=∠EAC=22.5°,
∴∠ECD=67.5°,
∴∠DEC=∠DCE=67.5°,
∴DE=CE,
∴△DEC是等腰三角形,
∵∠BEF=∠BFE=67.5°,
∴BE=BF,
∴△BEF是等腰三角形.

25.某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
【考点】一元一次不等式的应用;二元一次方程组的应用.
【分析】(1)首先设A种型号计算器的销售价格是x元,A种型号计算器的销售价格是y元,根据题意可等量关系:①5台A型号和1台B型号计算器,可获利润76元;②销售6台A型号和3台B型号计算器,可获利润120元,根据等量关系列出方程组,再解即可;
(2)根据题意表示出所用成本,进而得出不等式求出即可.
【解答】解:(1)设A种型号计算器的销售价格是x元,B种型号计算器的销售价格是y元,由题意得:
![]() ,
,
解得:![]() ;
;
答:A种型号计算器的销售价格是42元,B种型号计算器的销售价格是56元;
(2)设购进A型计算器a台,则购进B台计算器:(70﹣a)台,
则30a+40(70﹣a)≤2500,
解得:a≥30,
答:最少需要购进A型号的计算器30台.
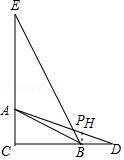
26.已知,AB是⊙O的直径,AE、AF是弦,BC是⊙O的切线,过点A作AD,使∠DAF=∠AEF.
(1)如图(1),求证:AD∥BC;
(2)如图(2),若AD=BC=AB,连接CD,延长AF交CD于G,连接CF,若G为CD中点,求证:CF=CB;
(3)如图(3),在(2)的条件下,点I在线段FG上,且IF=AF,点P在![]() 上,连接BP并延长到L,使PL=PB,连接AL,延长EA、BI交于点K,已知∠BAK+∠ABL=180°,∠ABI+∠BAL=90°,⊙O的半径为
上,连接BP并延长到L,使PL=PB,连接AL,延长EA、BI交于点K,已知∠BAK+∠ABL=180°,∠ABI+∠BAL=90°,⊙O的半径为![]() ,求四边形ALBK的面积.
,求四边形ALBK的面积.
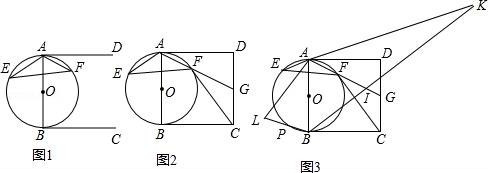
【考点】圆的综合题.
【分析】(1)连接BF,根据圆周角定理得到∠CBF=∠BAF,∠ABC=90°,等量代换得到∠BAD=∠DAF+∠BAF=∠ABF+∠CBF=∠ABC=90°,即可得到结论;
(2)连接BF,由(1)的结论推出四边形ABCD是正方形,得到tan∠DAG=![]() ,设正方形ABCD的各边长为2a,求得tan∠ABF=
,设正方形ABCD的各边长为2a,求得tan∠ABF=![]() ,根据勾股定理得到AG=
,根据勾股定理得到AG=![]() a,求得tan∠CFG=
a,求得tan∠CFG=![]() 即可得到结论;
即可得到结论;
(3)连接AP,BF,由AB是⊙O的直径,得到AP⊥BL,根据AB是⊙O的直径,得到BP⊥AI,求得tan∠ABF=tan∠DAG=tan∠IBF=![]() ,得到tan∠LAP=tan∠BAP=
,得到tan∠LAP=tan∠BAP=![]() ,根据已知条件得到∠PAB=∠KAD,设BK与⊙O交于H,连接AH,过K作KK´⊥AB解三角形得到AH=
,根据已知条件得到∠PAB=∠KAD,设BK与⊙O交于H,连接AH,过K作KK´⊥AB解三角形得到AH=![]() ,BH=
,BH=![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() =
=![]() ,求得AK′=
,求得AK′=![]() ,KK′=
,KK′=![]() ,于是得到结论.
,于是得到结论.
【解答】解:(1)连接BF,如图1所示:
∵AB是⊙O的直径,BC是⊙O的切线,
∴∠CBF=∠BAF,∠ABC=90°,
∵∠AEF=∠ABF,∠DAF=∠AEF,
∴∠ABF=∠DAF,
∴∠BAD=∠DAF+∠BAF=∠ABF+∠CBF=∠ABC=90°,
∴AD∥BC;
(2)如图2,连接BF,
由(1)知:∠BAD=∠ABC=90°,AD∥BC,
∵AD=BC=AB,
∴四边形ABCD是正方形,
∵G为CD中点,
∴tan∠DAG=![]() ,
,
设正方形ABCD的各边长为2a,
∵∠ABF=∠DAF,
∴tan∠ABF=![]() ,
,
∴BF=2AF,
∵AF2+BF2=AB2,
∴5AF2=4a2,
∴AF=![]() ,
,
∵AG=![]() =
=![]() =
=![]() a,
a,
∴FG=![]() ,
,
∴tan∠CFG=![]() ,
,
∴∠CFG=∠ABF,∠CFB=∠CBF,
∴CB=CF;
(3)如图3,连接AP,BF,
∵AB是⊙O的直径,
∴AP⊥BL,
∵LP=BP,
∴∠LAP=∠BAP,
∵AB是⊙O的直径,
∴BP⊥AI,
∵IF=AF,
∴∠ABF=∠IBF,
∴tan∠ABF=tan∠DAG=tan∠IBF=![]() ,
,
又∵∠ABI+∠BAL=90°,
∴∠LAP+∠BAP=45°,
∴tan(∠LAP+∠BAP)=![]() =1,
=1,
tan∠LAP=tan∠BAP=![]() ,
,
∵∠BAK+∠ABL=180°,
∴∠BAK+90°﹣∠PAB=180°,
∴∠BAK=90°+∠PAB,
又∴∠BAK=90°+∠KAD,
∴∠PAB=∠KAD,
设BK与⊙O交于H,连接AH,过K作KK´⊥AB,
∵tan∠ABF=![]() ,AB=
,AB=![]() ,
,
∴BF=AI=2![]() ,
,
∵AB=BI,
∴AH=![]() ,BH=
,BH=![]() ,
,
∵△ABH∽△BKK′,
∴![]() =
=![]() ,
,
∵KK′∥AD,
∴∠K′KA=∠DAK=∠BAP,
∴![]() =
=![]() ,
,
∴AK′=![]() ,
,
∴KK′=![]() ,
,
∴S四边形ALBF=S△ALB+S△ABK=![]() BL•AP+
BL•AP+![]() AB•KK′=3+12=15.
AB•KK′=3+12=15.
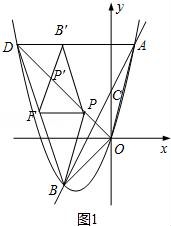
27.如图,二次函数y=ax2+bx(a≠0)的图象经过点A(1,4),对称轴是直线x=﹣![]() ,线段AD平行于x轴,交抛物线于点D.在y轴上取一点C(0,2),直线AC交抛物线于点B,连结OA,OB,OD,BD.
,线段AD平行于x轴,交抛物线于点D.在y轴上取一点C(0,2),直线AC交抛物线于点B,连结OA,OB,OD,BD.
(1)求该二次函数的解析式;
(2)设点F是BD的中点,点P是线段DO上的动点,将△BPF沿边PF翻折,得到△B′PF,使△B′PF与△DPF重叠部分的面积是△BDP的面积的![]() ,若点B′在OD上方,求线段PD的长度;
,若点B′在OD上方,求线段PD的长度;
(3)在(2)的条件下,过B′作B′H⊥PF于H,点Q在OD下方的抛物线上,连接AQ与B′H交于点M,点G在线段AM上,使∠HPN+∠DAQ=135°,延长PG交AD于N.若AN+B′M=![]() ,求点Q的坐标.
,求点Q的坐标.
【考点】二次函数综合题.
【分析】(1)根据二次函数y=ax2+bx(a≠0)的图象经过点A(1,4),对称轴是直线x=﹣![]() ,列出方程组即可解决问题.
,列出方程组即可解决问题.
(2)如图1中,首先求出直线AC与抛物线的交点B坐标,再证明DP′=PP′,推出四边形BFB′P是菱形,在RT△POB中求出OP即可解决问题.
(3)如图2中,过A作AI⊥HP,可得四边形AB′HI是正方形,过A作AL∥PN,连接ML,在Rt△MHL中,由ML2=MH2+HL2列出方程即可解决问题.
【解答】解:(1)由题意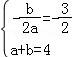 ,解得
,解得![]() ,
,
∴二次函数的解析式为y=x2+3x.
(2)如图1中,∵A(1,4)C(0,2),
设直线AC解析式为y=kx+b,则![]() 解得
解得![]()
∴直线AC 解析式为y=2x+2,
由![]() 解得
解得![]() 或
或![]()
∴B(﹣2,﹣2),∵D(﹣4,4)
∴BD=![]() ,
,
∵DF=FB,
∴S△DFP=S△BFP,
∴S△PFP′=![]() S△PBD,
S△PBD,
∴S△DP′F=S△PP′F
∴PP′=DP′,
∴PB∥P′F,
∴∠B′FP=∠PFB=∠FPB,
∴PB=BF=FB′,
∴四边形BFB′P是平行四边形,
∵BF=BP
∴四边形BFB´P是菱形,
∴PB=![]() ,
,
∵P在y=﹣x上,OB=2![]() ,
,
在RT△OPB中,OP=![]() =
=![]() ,
,
∴P(﹣1,1)
∴PD=![]()
(3)如图2中,由(2)得F(﹣3,1),P(﹣1,1)B’(﹣2,4).
过A作AI⊥HP,可得四边形AB′HI是正方形,过A作AL∥PN,连接ML.
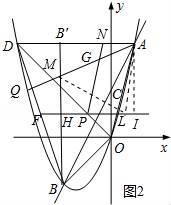
由∠HPN+∠DAQ=135°得∠MGP=45°
∴∠MAL=45°,设B′M=m,则AN=![]() ﹣m,
﹣m,
∴PL=![]() ﹣m,
﹣m,
∴LI=m﹣![]() ,
,
∴ML=B′M+LI=2m﹣![]() ,
,
在Rt△MHL中,∵ML2=MH2+HL2,
(2m﹣![]() )2=(
)2=(![]() ﹣m)2+(3﹣m)2
﹣m)2+(3﹣m)2
解得m=![]()
∴M(﹣2,![]() )
)
∴直线AM解析式为:y=![]() x+
x+![]() ,
,
由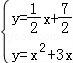 解得
解得![]() 或
或![]() ,
,
∴Q(![]() ,
,![]() ).
).

孔乙己是贫困潦倒的知识分子。在书中,孔乙己是一个知识分子,满口“之乎者也”,但是他很穷,还窃书,说过“读书人的事,怎么能叫窃,”被人嘲笑,他...

自然界产生氧气的化学方程式:光合作用的反应式为6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反应和暗反应两个过程。需要具备光...

有的高校没有条件,只要学业水平成绩都合格就可以,比如中国科学院大学。有的需要平常学习考试成绩,比如北京外国语大学要求高三第一学期期末成绩在全...

在四则运算中,表示计算顺序,在小括号之后、大括号之前;表示两个整数的最小公倍数;表示取未知数的整数部分;在函数中,表示函数的闭区间;在线性代...

济南开设的最好的职高学校有:济南方信集团职业高中、济南公共交通职业高中。济南市公共交通职业高级中学是由济南市公共交通总公司承办,业务属济南市...

实然:是说事物实际上就是这样的,但不同于现实性(现实性指其有合理性和客观性);应然:就是应该是怎么样的意思,比如说这件事,就应该是那样的结果...

地中海气候一种夏季炎热干燥、冬季温和多雨,雨热不同期的气候类型。地中海气候冬季受西风带控制,锋面气旋频繁活动,气候温和,最冷月的气温在4-1...

碱石灰,又称钠石灰,碱石灰是白色或米黄色粉末,疏松多孔,是氧化钙(CaO,大约75%),水(H₂O,大约20%),氢氧化钠(NaOH,大约3...